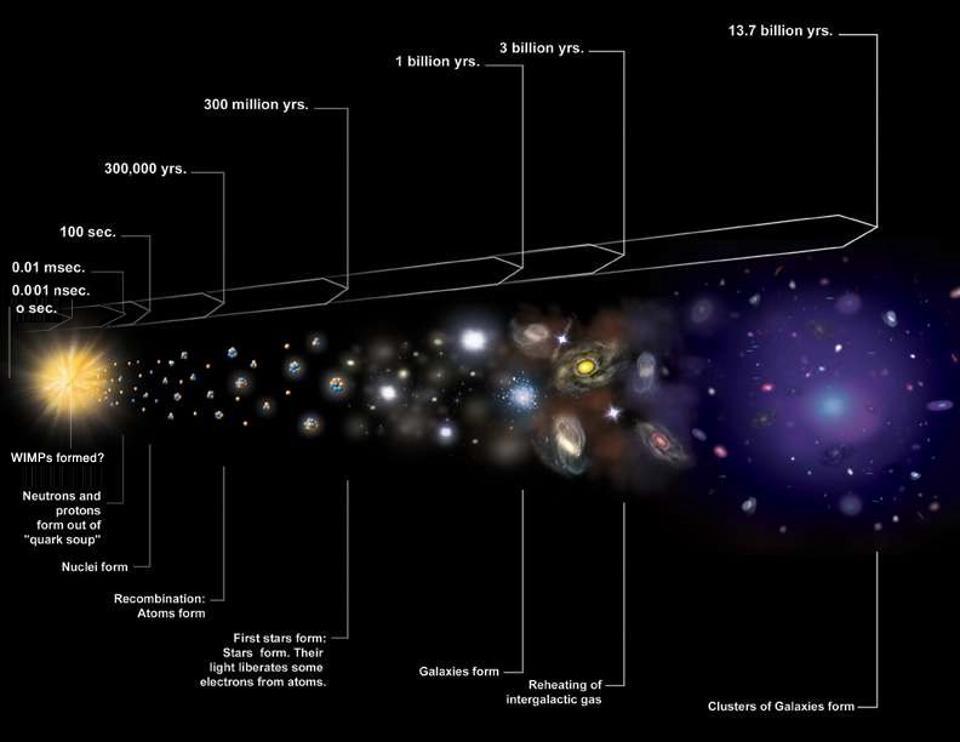
Why “distance” is not what it seems in the expanding Universe
- If you look at a distant object and you know its intrinsic properties, you'd think you can determine its distance by measuring its brightness, angular size, or the travel time of the light.
- If the Universe weren't expanding, and instead were more like what Newton had envisioned, all three of these methods would be correct and in agreement.
- In our actual Universe, however, not only are all three different from one another, none of them match the actual "distance" without corrections. Here's why.
Take a look at any object, and what you see will be dependent on how far away it is from you. In reality, this object will have specific physical properties: size, color, brightness, etc., and will be located a particular distance from you. Typically, your way of detecting this object will be based in electromagnetic radiation, also known as light. The light that you see is the light arriving at your eyes right now, but that light would have been emitted by this object a certain amount of time in the past: the time it takes that light to travel from that object to your eyes.
In addition, the object will appear smaller and less bright the farther it is away from you. Light spreads out in a sphere once it leaves the source that generated it, and hence the farther it is from you, the fainter it appears. In addition, all physical objects take up a particular physical size, so the farther away they are, the smaller — in terms of angular size — they appear to you.
But these relationships, which are straightforward in our everyday experience, are wildly counterintuitive in the expanding Universe. Light-travel time, brightness, and angular size all defy our expectations. In a very real way, distances are not as they appear in the expanding Universe. Here’s how to make sense of them.

The way we normally conceive of things is the same way that Euclid and Newton did: as though the world was defined by some sort of fixed three-dimensional space, where you could define all objects by their position. In classical physics, as well as in Euclidean geometry, all observers everywhere can agree on the definition of what position and location mean: both in an absolute sense as well as in a relative sense. If that were the case for our actual, physical Universe, then everything would be simple and straightforward when it came to measuring the cosmic distances to various objects.
- An object’s angular size would simply be determined by its physical size at a physical distance. If you knew how big it actually was and could measure its angular size, you can determine how far away it is.
- An object’s apparent brightness would simply be determined by its intrinsic brightness at a physical distance. If you knew how luminous it was and could measure how bright it appeared, you could determine its distance.
- And if you looked back at an object and knew how long had elapsed from when the light was emitted until you observed it, you could know how far away it was. Just multiply the light-travel time by the speed of light, and there you have its distance.

It seems so simple and straightforward that it couldn’t possibly be wrong. Unless, that is, one of the underlying assumptions behind this reasoning were false, and in this case, it is.
The falsehood?
Assuming that our three-dimensional space is fixed, and that observers at different locations in space and/or time would agree on what “positions” actually are, is the problem. Space, among many other properties in the Universe, is relative to the observer. In this case, “relative” means:
- what you perceive changes as your velocity changes,
- what you perceive changes as time passes,
- what you perceive changes dependent on the distribution of masses in the nearby Universe,
- and what you perceive changes, on a global scale, as the Universe itself expands.
Although all of these components play a role, the largest role is played by the expanding Universe.
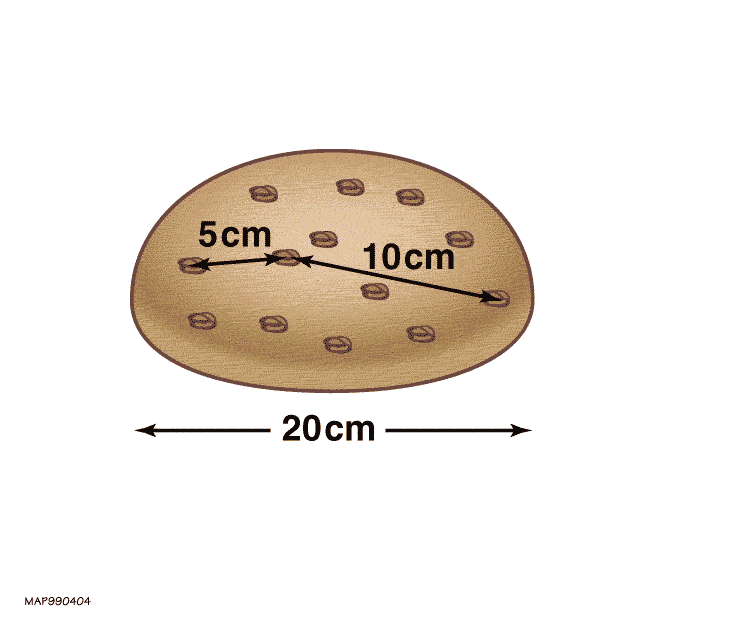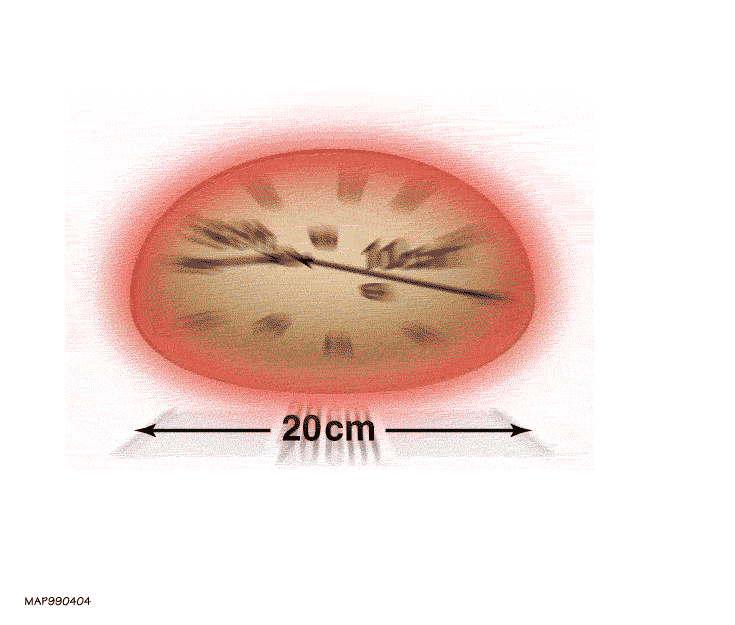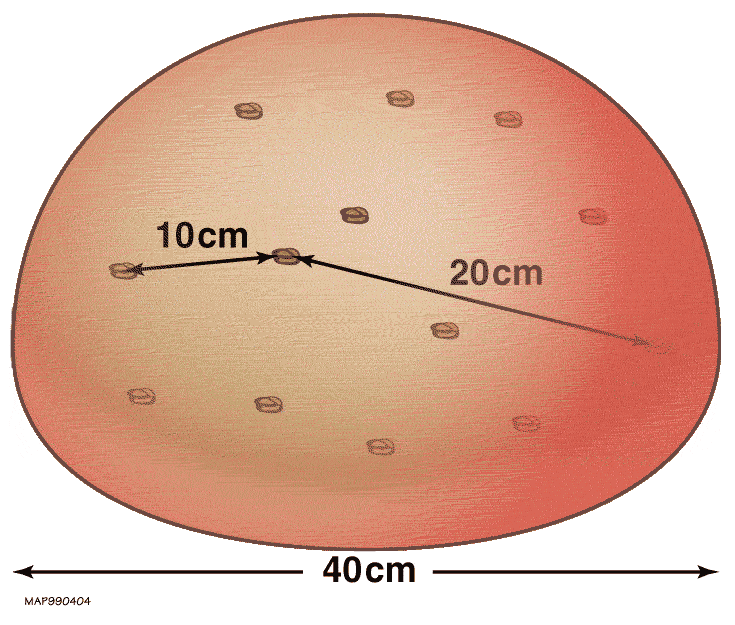
Perhaps the best analogy for the expanding Universe is a loaf of leavening raisin bread. Imagine you have a ball of dough with raisins distributed all throughout it. Imagine the ball is in the zero-gravity environment of space, so that no direction or dimension is preferred over any other. And furthermore, I want you to imagine that the dough itself is transparent, so that you could see “through it” to the individual raisins inside.
Each raisin is like a galaxy or other luminous object that’s gravitationally bound together, but that isn’t gravitationally bound up as part of a larger structure. The dough is like the fabric of space: it expands over time.
If you were to imagine that you, yourself, were located on one of the raisins, what would you see? At each moment, you’d see the raisins as they were relative to you: as the light from them that traveled through the “expanding dough” was just arriving. Only, because of that expansion, the light you saw wouldn’t have precisely the same properties as the light that was emitted.
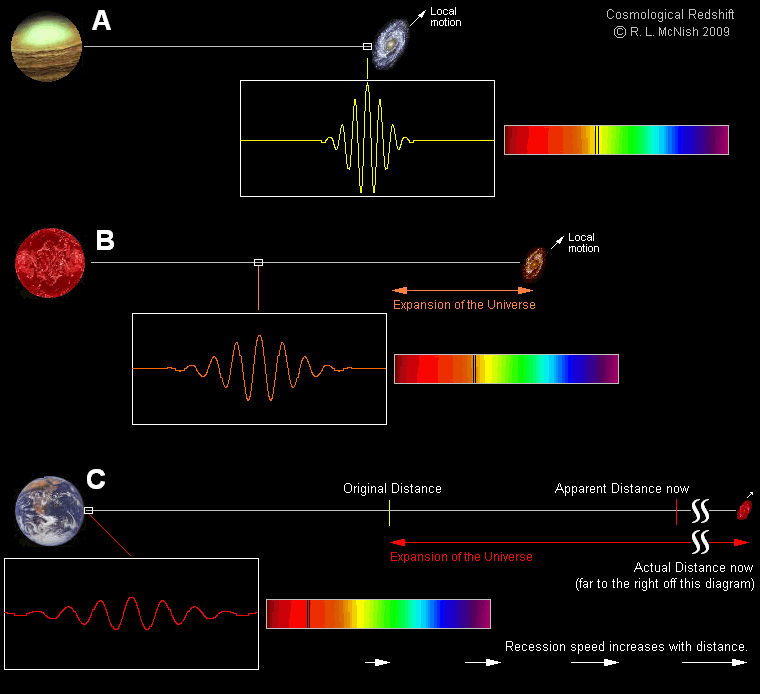
The first and most obvious thing that occurs is that the light gets affected by the expansion of the Universe. As the fabric of space “stretches” while the light journeys through it, the light itself also stretches: to longer and longer wavelengths. Longer wavelengths mean redder colors, cooler temperatures, and lower energies, so it really is true that the Universe cools as it expands. It also means that if we were to take three snapshots of the Universe:
- at the moment the light was emitted from any particular “raisin” in this raisin bread,
- at the moment where the distance between the emitting “raisin” and the observer “raisin” equaled the light-travel time (multiplied by the speed of light) that the light wave will traverse over its entire journey,
- and at the moment the light arrives at the observer “raisin” in the raisin bread,
we would obtain three different answers to the question of “How far away are these two raisins from one another?” The light was emitted back in the distant past, and was emitted farther back in time the farther away the emitting raisin is located. And although the light takes a journey (that we can measure in years) through the Universe, by the time that light arrives, the expansion of the Universe has pushed that object so that it’s much farther away than either the light-travel time or the initial separation distance would indicate.

Another thing that happens, although it isn’t necessarily obvious from the raisin bread analogy, is that the expansion rate itself changes as the Universe evolves. At any particular moment in time, there are only three things that determine how quickly the Universe expands:
- the sum of all the matter-and-energy, in all its various forms, at the particular location in space you’re occupying,
- the initial expansion rate as it was at the start of the hot Big Bang,
- and what the curvature of space is, right now, at the particular location in space that you’re occupying.
If the initial expansion rate was the same everywhere, and the curvature of space is negligible everywhere, then the biggest factor in the evolution of light that travels through the expanding Universe is how the various types of energy change, relative to one another, in terms of density. Fortunately for all of us, the last few decades in cosmology have been revolutionary for teaching us both what our Universe is made out of, including in what ratios at all sorts of different times, and how its expansion rate has changes over its history.
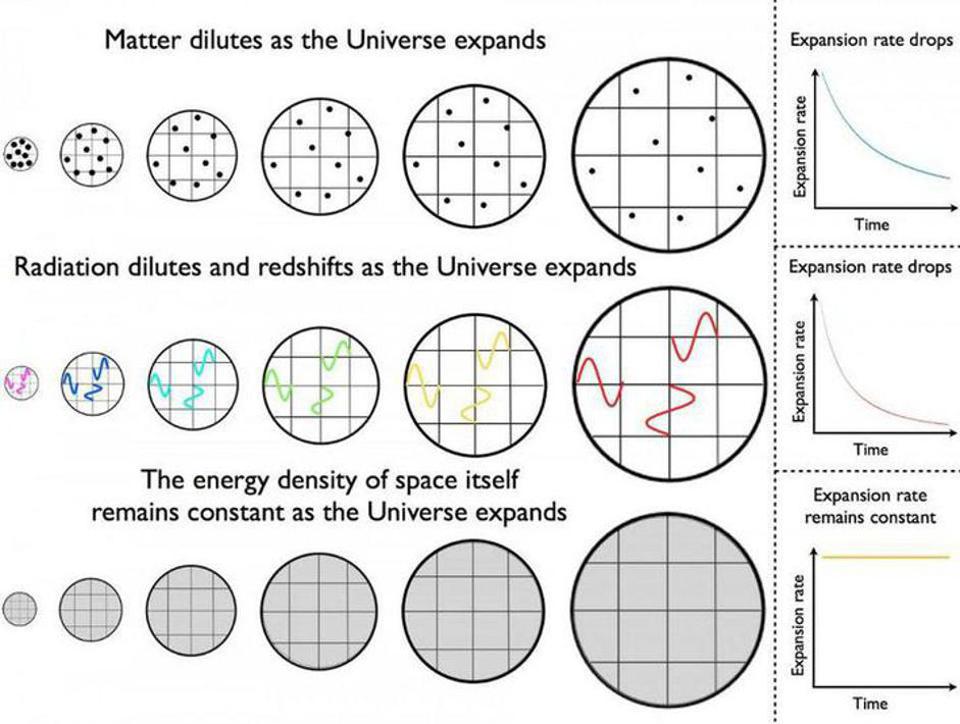
What we’ve learned is that, today, our Universe is made out of:
- 68% dark energy, which is a form of energy inherent to the fabric of space itself,
- 27% dark matter, which is massive, clumps and gravitates, but always moves slow compared to the speed of light,
- 4.9% normal matter, which is massive, clumps and gravitates, interacts collisionally with both itself and radiation, and moves fast compared to the speed of light at very early times,
- 0.1% neutrinos, which are massive, clump and gravitate at cosmically late times, but which move close to the speed of light for at least several million years,
- and 0.01% photons, which are massless and always behave as radiation.
If you behave like matter, your density drops as the Universe expands, since density is mass over volume and the volume increases. If you behave like radiation, your density drops more quickly than matter’s density drops, since not only does the volume increase, but the wavelength of your radiation gets stretched by the expanding Universe. And if you behave like dark energy, your energy density remains constant, since new space gets created when the Universe expands, preventing the density from decreasing.
When you factor in everything we know about the expanding Universe, we can immediately learn some valuable lessons about what distance actually is, and how it differs from our Euclidean/Newtonian prejudices.

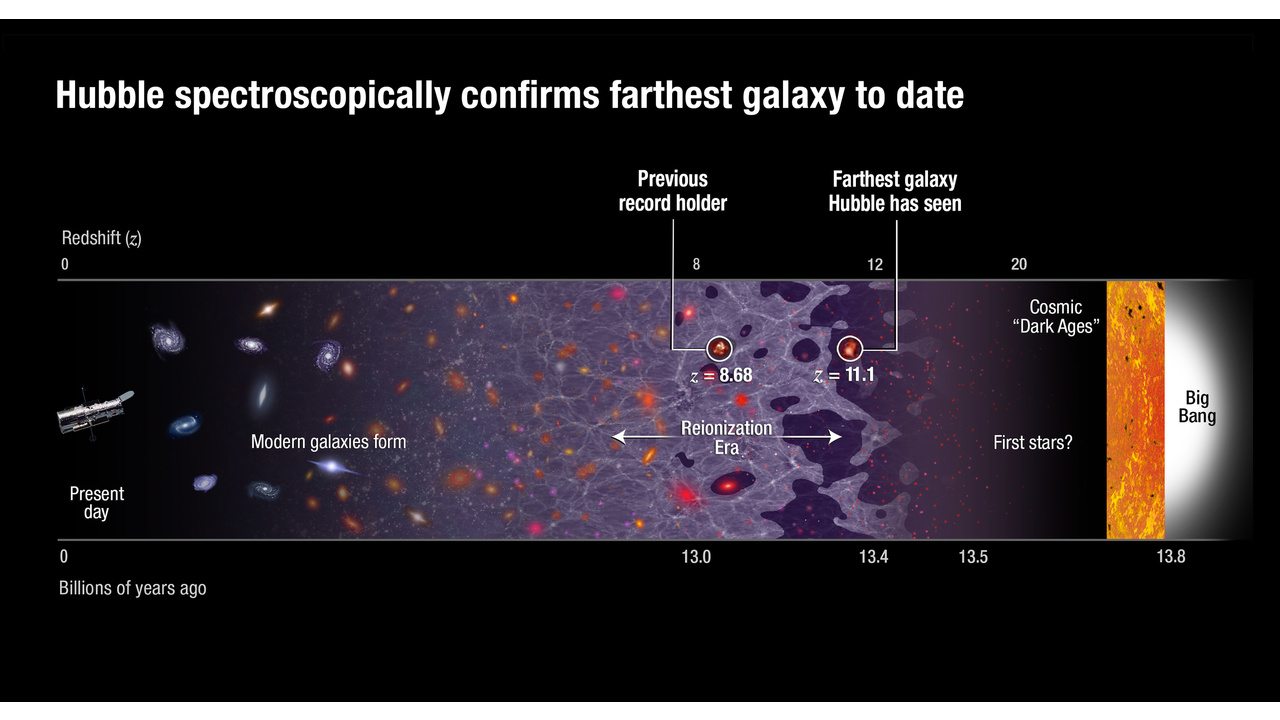
Lookback time. Have you ever wondered why we say things like, “we see this object as it was 13.4 billion years ago, and it’s 32 billion light-years away”? That’s because of how distances evolve in the expanding Universe. When the light was first emitted, the Universe was much smaller, and that object was not even 1 billion light-years away from us. As that light traveled to us, the Universe expanded; initially, the light got farther away, but as the expansion rate slowed, it caught up to us. Finally, today, after a journey of 13.4 billion years, the light arrives. But the object itself is now even farther away: 32 billion light-years.
As we look to farther and farther distances, the difference between “lookback time” in years and “actual distance, today” in light-years gets progressively greater, as the expanding Universe has a more pronounced effect. For example:
- Light arriving from 100 million years ago corresponds to an object presently 101 million light-years away.
- Light arriving from 1 billion years ago corresponds to an object presently 1.036 billion light-years away.
- Light arriving from 5 billion years ago corresponds to an object presently 6.087 billion light-years away.
- Light arriving from 10 billion years ago corresponds to an object presently 16.03 billion light-years away.
- Light arriving from 13.78 billion years ago corresponds to an object presently 41.6 billion light-years away.
The important takeaway is that the distance to an object is not the light-travel time multiplied by the speed of light; it’s greater in the expanding Universe.

Luminosity distance. The farther away an object is, the fainter it is; that’s exactly what you’d expect. But the farther away you go, as you measure just how faint it gets, you’ll progressively begin to discover that things get fainter faster than you expected. This is because the light is affected by the curvature of space, by the cosmological redshift, and by time dilation of cumulatively intervening matter. If the Universe were static, an object that was twice as distant would appear to be just one-quarter the brightness, but in reality, it’s even less bright than that, largely due to the “redshift” factor.
One of the most surprising finds in all of human history was the discovery of dark energy, which was revealed by the study of ultra-distant supernovae. The fact that the expansion of the Universe, at very late times, is dominated by a form of energy (dark energy) that doesn’t get less dense as the Universe expands is why objects get fainter, more severely, the longer it takes their light to arrive at our eyes. This isn’t necessarily intuitive, but it’s not the biggest surprise in the Universe.
Arguably, that designation goes to the last type of distance measure we could use: one based on angular size.

Angular diameter distance. You’d think this would be the most straightforward: know how big an object is, intrinsically, then measure how large it appears on the sky, and you can calculate how far away it is. Only, that’s no good, because for every angular size that you’d see, there are actually two distances that the object could be at: one closer to you and one farther away.
Why is this the case? Because, way back when the Universe was younger, the objects that are now very distant were once much nearer, and hence, they appeared to take up a much larger angle on the sky. Even though the Universe has expanded since then, it once expanded faster than light could travel, and only after the expansion rate drops does the light begin to “catch up” to us.
In other words, as you look farther away, objects appear smaller and smaller until a critical point: a minimum size that objects will appear in our Universe, which occurs for objects that are somewhere around 15 billion light-years away. Beyond that, they start to appear larger again; if something comes from us close by or very far away, they will appear to be the same angular size on the sky.

This is not a bug with the expanding Universe; it is a feature. It means that if we can build a telescope to resolve objects that are a certain size across — a thousand light-years, or a hundred, or ten, or one — that are presently 15 billion light-years away, that telescope would be able to see every object in the Universe at that resolution or better. If you want to build a large space telescope, like the National Academies just rated as their highest priority for NASA astrophysics, this is what it gets you: superior resolution all across the observable Universe.
In the expanding Universe, distant objects are fainter than they appear. They’re farther away than they appear. But in terms of angular size, once you get beyond a certain distance, they actually appear larger than they truly are. We can exploit this, if we’re clever enough and willing to invest our resources in it, to probe more distant objects in the Universe to better accuracy and resolution than ones that are closer to us. When it comes to seeing across the great cosmic expanse, there are precious few ways that nature gives us a helping hand. By making ultra-distant galaxies appear larger than they actually are, the expanding Universe highlights one undoubtable way that the cosmos, at least in terms of discovery potential, has been kind to us.