How B-mesons are threatening to break the Standard Model

Most of us, when we think about the Standard Model, think about the fundamental particles and forces that make up the Universe. That’s not a bad thing; that’s largely correct! Within the Standard Model, the prescription for the full suite of particles that ought to exist is:

• six flavors of quarks (up, down, strange, charm, bottom, top),
• three flavors of charged leptons (electron, muon, tau),
• three flavors of uncharged leptons (electron neutrino, muon neutrino, tau neutrino),
• the photon (for the electromagnetic interaction),
• the W-and-Z bosons (for the weak nuclear interaction),
• the gluons (for the strong nuclear interaction),
• and the Higgs boson (the particle associated with the Higgs field).

The quarks and leptons combine together to make the composite structures we’re familiar with, including protons, neutrons, and atoms, while the bosons (all the other particles) mediate the forces between them.

Only one of those forces, however, the weak nuclear force, is capable of changing the flavor (or species) of a quark or lepton from one type to another. The goal of particle accelerators and colliders, such as the Large Hadron Collider at CERN, isn’t just to try to create the heavy, exotic particles that only live for a fraction-of-a-second before decaying, but to study those decays in gory detail. In addition to giving us the particles and their interactions, the Standard Model also tells us both which types of decays are allowed and forbidden (for example, neither the Z-boson nor any other “neutral current” can change a quark’s or lepton’s flavor), as well as how often each type of decay (known as a branching ratio) should occur.

It’s for that reason that B-mesons are so interesting. For the first time, an aggregation of all the LHC data where B-mesons (mesons containing a bottom quark or antiquark) decay has been performed, and a tantalizing hint that may ultimately break the Standard Model has now appeared. Here’s why particle physicists are — justifiably — so excited about this discovery.

Deep underground, this tunnel is part of interior workings of the LHC, where protons pass each other at 299,792,455 m/s while circulating in opposite directions: just 3 m/s shy of the speed of light. Particle accelerators like the LHC consist of sections of accelerating cavities, where electric fields are applied to speed up the particles inside, as well as ring-bending portions, where magnetic fields are applied to direct the fast-moving particles toward either the next accelerating cavity or a collision point.

When most of us think about the Large Hadron Collider (LHC), we think about the energy frontier: the highest-energy, shortest-lived particles that exist in nature. The LHC is an enormous particle accelerator — the largest ever built on Earth — with a ring that extends for some 27 kilometers in circumference. It also boasts the strongest bending magnets ever used in a large-scale particle accelerator, with magnetic fields of 8.4 Tesla: more than 100,000 times as strong as Earth’s natural magnetic field. This allows the LHC’s protons, which are accelerated to the highest energies that any particle has ever achieved in a laboratory, to produce great numbers of exotic, heavy, unstable, short-lived particles.

These include top quarks, W-and-Z bosons, and of course the long-elusive (and only recently discovered) final “missing piece” in the Standard Model: the Higgs boson. Discovered at the start of the 2010s by both the CMS and ATLAS collaborations — the two “main” detectors at the LHC — thousands upon thousands of Higgs bosons have been created at the LHC, with these detectors measuring their decay products. So far, when all the data is summed together, there are no departures from the predictions of the plain old Standard Model Higgs boson. The Standard Model remains intact for now, at least, as far as the Higgs particle itself goes.

The observed Higgs decay channels vs. the Standard Model agreement, with the full suite of Run 1 data from ATLAS and CMS included. The agreement is astounding, and yet frustrating at the same time, as no evidence for either a second Higgs boson or for a non-Standard Model Higgs boson has yet arisen.

But CMS and ATLAS aren’t the only detectors at the LHC, and while the Higgs boson (along with the top quark and the W-and-Z bosons) may be the heaviest, most difficult-to-create among the Standard Model particles, they aren’t the only ones of interest. Whenever you collide two particles together, whether they’re composite (like protons) or fundamental (like electrons), that collision has the opportunity to create new particles via Einstein’s E = mc². If there’s enough available energy — i.e., “left over” energy after the energy required to conserve all mandatory quantities is accounted for — then new particles, including new quarks/antiquarks, new leptons/antileptons, and/or new bosons can all be created.

The hardest particles to create are the heaviest, most massive ones:

• the top quark and antiquark (at ~173 GeV/c² each),
• the Higgs boson (at ~126 GeV/c²),
• the Z-boson (at ~91 GeV/c²),
• and the W-bosons (both positively and negatively charged versions, at ~80 GeV/c² each).

These particles normally decay rapidly but travel, at least initially after their creation, rather slowly compared to the speed of light. Because they require so much energy to bring into existence, even at an accelerator like the LHC, it’s very difficult to create them with a lot of kinetic energy. It’s only the lighter particles, the decay products of these very heavy particles, or the remnants of the initial protons (which themselves move at around 299,792,455 m/s before the collision) that travel quickly.

The rest masses of the fundamental particles in the Universe determine when and under what conditions they can be created, and also relate to how long they can survive after their creation during the hot Big Bang. The more massive a particle is, the less time it can spontaneously be created in the early Universe, and the shorter its lifetime will be.

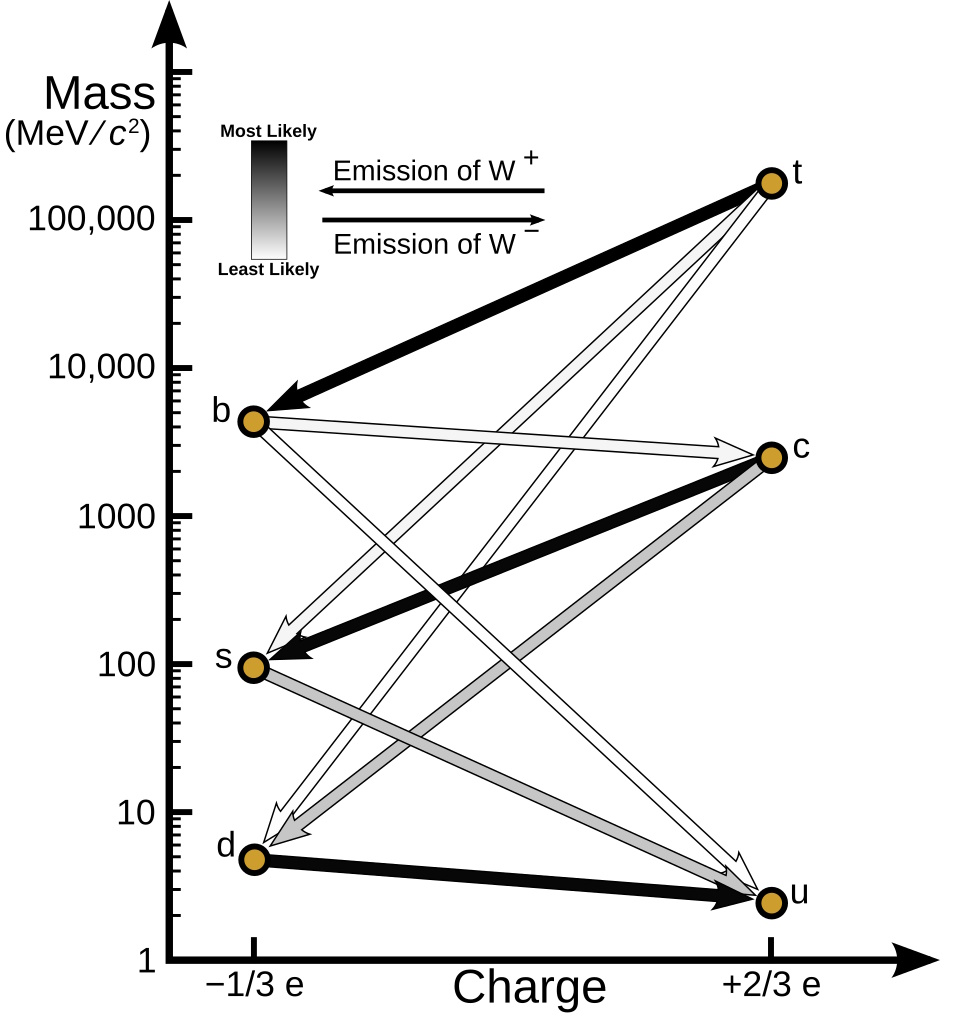
But if you push these four species of particle aside and ask, “What’s the next heaviest particle?” the answer is kind of surprising: it’s the bottom quark and antiquark, but it’s only about 5% the mass of the W-bosons, with a mass between ~4 and 5 GeV/c². Unlike the top quark, which decays after less than a yoctosecond (10^-24 seconds) — which is too short of a timescale to even form hadrons like baryons and mesons — the bottom quark lives for about a picosecond (10^-12 seconds), which might seem incredibly short, but it’s more than a trillion times longer-lived than the heaviest quark. As a result, the bottom quark (and antiquark) always form hadrons, whether a baryon, an antibaryon, or a meson.

Being relatively light, at least compared to the heaviest Standard Model particles, means that particles containing bottom quarks or antiquarks created at the LHC (which, remember, collides protons with protons at ~14 TeV of energy, or ~14,000 GeV) always move very close to the speed of light. These can still be detected by CMS or ATLAS, and are, but there’s another detector that’s even better suited to measuring these bottom-quark (or bottom-antiquark) containing hadrons: LHCb. This enormous detector, 5600 metric tonnes in mass and more than 21 meters (65 feet) long, is managed by a team of more than 1500 scientists, enabling them to reconstruct the particle tracks and debris, as well as particle decays, that result from bottom quark (or antiquark) containing composite particles.

The LHCb detector, at 5600 metric tonnes, is 21 meters long, 10 meters high, and 13 meters wide, optimized for detecting and studying particles (and their subsequent decays) that contain b-quarks inside them. At present, there are over 1500 scientists, engineers, and technicians that work on the LHCb collaboration.

According to the Standard Model, there are rules that these particles must obey. A bottom quark (or antiquark) can only decay to products that include either an up quark (or antiquark) or a charm quark (or antiquark); no other possibilities are allowed. Electric charge needs to be conserved, as do the energy and momenta of all the products resulting from decays. And if you’re going to make a specific type of hadron — a meson — that contains a bottom quark (or antiquark), then the antiquark (or quark) that accompanies it inside the meson must be of the up, down, strange, charm, or bottom variety. Again, no other possibilities are allowed.

But the Standard Model has rules that are even more intricate than these: rules that govern the decays of particles that contain a bottom quark (or antiquark). In particular, mesons that pair a bottom quark/antiquark with one of the three very light antiquarks/quarks (up, down, or strange) can often decay into two other mesons, where pions (which are made of up-and-down quarks only, and include the positively charged π⁺, the neutral π⁰, and the negatively charged π^–) and kaons (which include one strange quark or antiquark, and come in four varieties: the K⁺, K^–, as well as two neutral kaons, the K-short and the K-long) are extremely common.

Although there are literally dozens of possible decays for these B-mesons (any meson that has at least one bottom quark or antiquark), the ones that decay into pions and/or kaons fall into two broad categories:

• a category where the total number of strange quarks and antiquarks doesn’t change during the decay,
• and a category where the total number of strange quarks and antiquarks changes by ±1.

This to-scale diagram shows the relative masses of the quarks and leptons, with neutrinos being the lightest particles and the top quark being the heaviest. No explanation, within the Standard Model alone, can account for these mass values.

One of the properties of the Standard Model that isn’t generally appreciated is known as flavor universality. This means that the interactions of the Standard Model apply equally, with the same strength and properties, to all the different species of particles of the same type. The interactions experienced by the electron, muon, and tau should be universal; that’s called lepton flavor universality. Since the early 2010s, there were serious experimental questions about whether lepton flavor universality was violated by B-meson decays that involved leptons (specifically, the muon or electron).

It was only in 2022 that scientists discovered a series of mis-identified backgrounds; once they were properly accounted for, lepton universality prevailed. B-meson decays, after over a decade of study, appeared consistent with the Standard Model after all.

However, quark flavor universality is a similar concept that has gotten far less attention. Under the strong, electromagnetic, and weak neutral current (Z-boson involving) interactions, the quark sector exhibits flavor universality as well. It’s true that B-meson decays are not universal, but that’s because there are specific rules within the Standard Model for how quarks mix together. Once you account for the parameters in the CKM-mixing matrix, it allows you to compute how frequently you expect B-mesons, whether they’re created with or without strange quarks/antiquarks inside, to produce a decay product that contains either the same number of strange quarks/antiquarks or for that number to differ by ±1 from the initial value.

This diagram shows the allowable decays of quarks in the Standard Model via the weak interaction. Note that bottom quarks (or antiquarks) can only decay to either charm or up quarks within the Standard Model, with charm quarks being the most common.

As the authors of a brand new paper, published in late November of 2024 in Physical Review Letters, note, all of the decays that involve B-mesons decaying to either:

• two pions,
• two kaons,
• or one pion and one kaon,

are related to one another by a flavor symmetry between up, down, and strange quarks: an example of what particle physicists specifically call a flavor SU(3) symmetry. 20 years ago, one needed to make assumptions and approximation about what was relevant and what could be ignored in order to calculate what this symmetry should imply as far as the different decay and branching ratios available to B-mesons.

Those assumptions and approximations are no longer necessary, however, as there’s now enough data about B-mesons to know:

• what the Standard Model’s predicted flavor SU(3) symmetry will yield for the ratios of these different types of decays,
• and whether the observed B-meson decays that go into either two pions, two kaons, or one pion and one kaon match those predictions,
• or whether the observed B-meson decays show a discrepancy with what the Standard Model predicts.

It’s a brand new type of “stress test” for the Standard Model: our modern picture of particle physics that has survived every other such stress test so far.

This event shows one example of a rare decay of a B-meson that involved an electron and positron as part of their decay projects, as observed by the LHCb detector. These lepton decay channels for B-mesons challenged the Standard Model in the past, but turned out to be a phantasm. Hadronic decay channels, however, still remain a potential Standard Model-challenging avenue.

The reason we can perform this type of stress test now, whereas we couldn’t before, is that only now do we have a sufficient number of measured observables to constrain all of the parameters that come along with the Standard Model and this particular flavor symmetry. When we ask about specific decays — i.e., when a particular species of B-meson decays to a specific set of products — we need a greater number of measured observables, including:

• branching ratios,
• direct CP asymmetries,
• and indirect CP asymmetries,

than we have unknown theoretical parameters, which include:

• magnitudes,
• and relative strong phases.

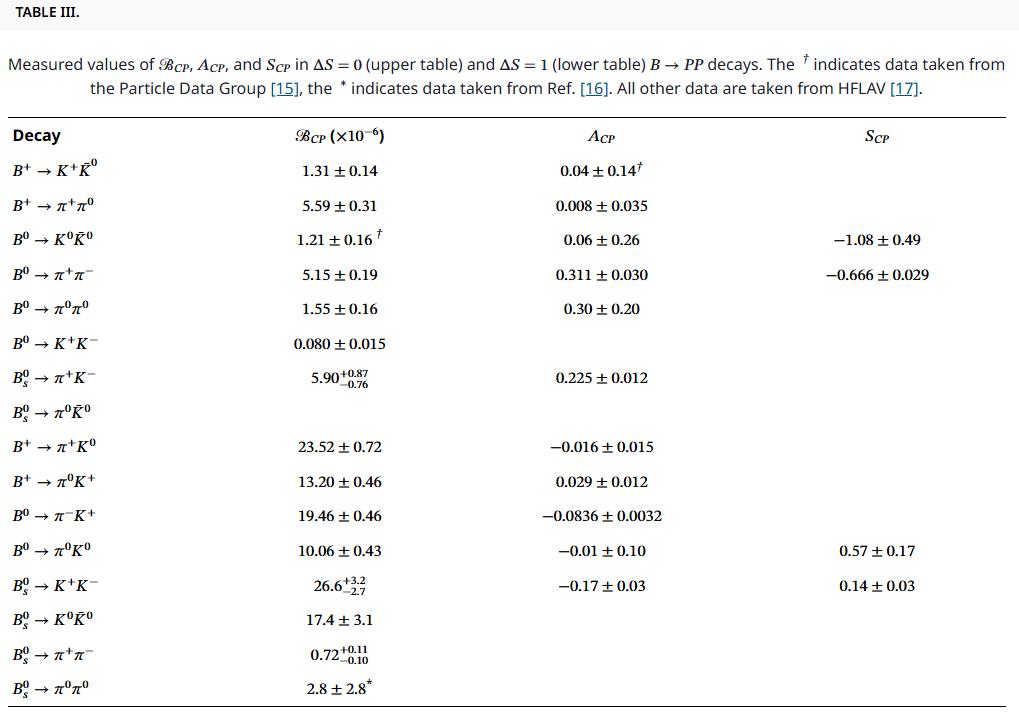
For decays where strangeness (the number of strange quarks/antiquarks) is conserved and for decays where strangeness is violated by ±1, there are 13 theoretical unknowns each: 7 magnitudes and 6 relative strong phases. It’s only now, in this newest analysis, that we have more measured observables (which provides relationships, like equations, between the unknowns) than there are unknowns: 15 measured observables for each. This is illustrated in the table below, lifted from the relevant article, where the upper half shows the strangeness-conserving option (you can count the 15 entries for measured parameters) and the lower half shows the strangeness-violating option (again, you can count the 15 entries).

The key table of the analysis, where strangeness-conserving decays of B-mesons (top half) and strangeness-violating decays of B-mesons (bottom half) each require 13 inputs. With 15 entries now robustly measured in each part of the table, we finally have sufficiently good data to test the Standard Model with B-meson decays.

That’s good; it means we can put our theory to an experimental test! We can see how well this data fits (or conflicts with) the Standard Model, and we can see it in a number of different ways. The three ways that are particularly interesting are:

1. to ask whether the strangeness-conserving decays are consistent with the Standard Model,
2. to ask whether the strangeness-violating decays are consistent with the Standard Model,
3. and then whether the strangeness-conserving and strangeness-violating decays are consistent with each other.

The answer to the first question, based on the latest data, is yes. And the answer to the second question, based on the latest data, is also yes. But the answer to the third question turns out to be no, at least according to this latest study.

The next question is then, if something doesn’t match, how significant is this discrepancy or inconsistency?

In particle physics, the gold standard to announce a discovery is given in terms of significance: 5-σ significance. If we get a robust signal that conflicts with the Standard Model at greater than 5-σ significance, then we’ve got compelling evidence that something in the world of particle physics disagrees with, and compels us to go beyond, the known physics that has governed our understanding of the Universe for more than half a century.

The leading contributions of the decay channels that conflict with the expected contributions from Standard Model physics in B-meson decays. Note that, at right, the assumption of additional constraints increases the significance, but the justifiability of those assumptions is not guaranteed.

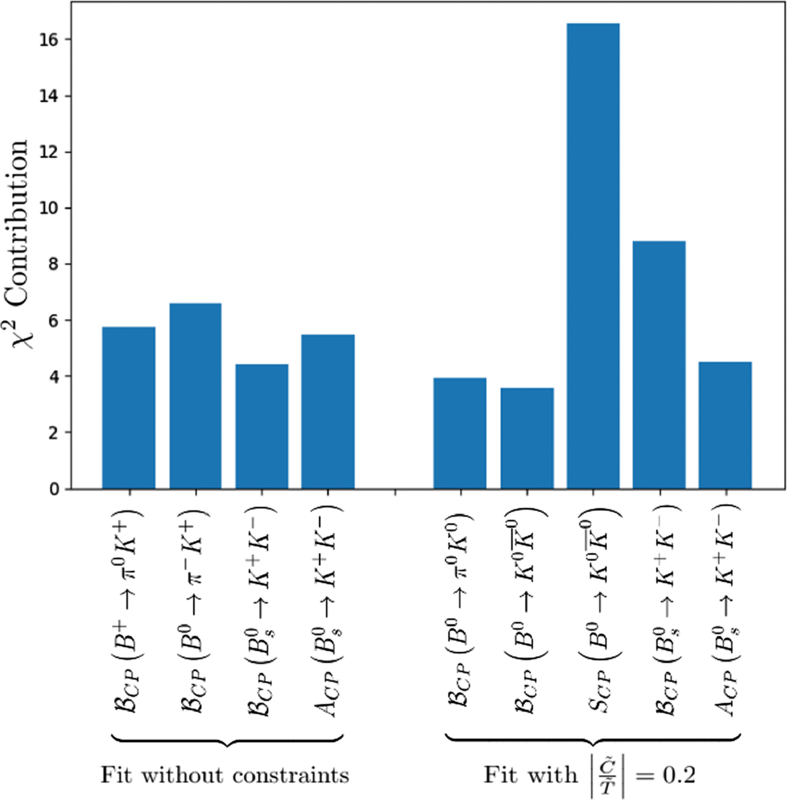
With no assumed additional constraints, which is the most conservative approach, this latest result comes in at 3.6-σ significance. With an assumed constraint coming from calculations of various parameters arising in QCD, that significance rises to 4.4-σ: tantalizingly close to that vaunted threshold, but a little more subject to systematic uncertainties and so not necessarily convincing to everyone. As the authors put it:

“To sum up, assuming unbroken flavor SU(3) symmetry, a global fit to all [B-mesons decaying to either two pions, two kaons, or a kaon and a pion] data finds a discrepancy with the [Standard Model’s SU(3) flavor symmetry predictions] at the level of 3.6𝜎. This discrepancy can be removed by allowing for [flavor symmetry]-breaking effects, but 1000% [flavor symmetry]-breaking is required, i.e., parameters that are equal in the [flavor symmetric] limit must now differ by a factor of 10. These results are group-theoretically rigorous—no dynamical assumptions have been made. […] These are the anomalies in hadronic 𝐵 decays. They strongly hint that new physics is present in these decays.”

It’s going to take more data and independent analyses of that data to confirm this, where perhaps someday the strength of this anomaly will indeed rise to the needed 5-σ threshold. The Standard Model still remains intact for now, but if nature is kind to us, this hint of beyond the Standard Model physics will point the way to a deeper understanding of our physical Universe.