Attoseconds aren’t fast enough for particle physics

One of the biggest news stories of 2023 in the world of physics was the Nobel Prize in Physics, awarded to a trio of physicists who helped develop methods for probing physics on tiny timescales: attosecond-level timescales. There are processes in this Universe that happen incredibly quickly — on timescales that are unfathomably fast compared to a human’s perception — and detecting and measuring these processes are of paramount importance if we want to understand what occurs at the most fundamental levels of reality.

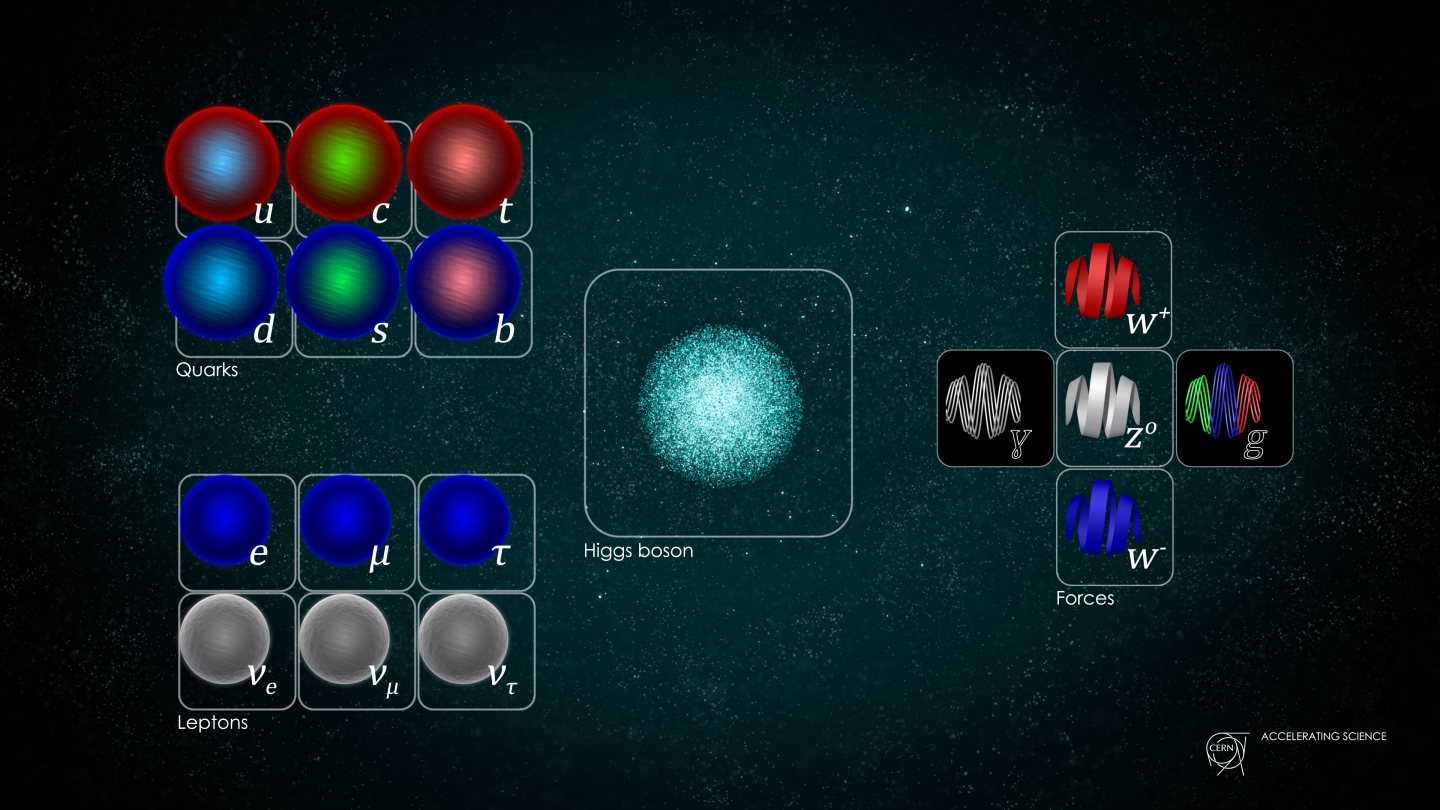
Getting down to attosecond-level precision is an incredible achievement; after all, an attosecond represents just 1 part in 10¹⁸ of a second: a billionth of a billionth of a second. As fast as that is, however, it isn’t fast enough to measure everything that occurs in nature. Remember that there are four fundamental forces in nature:

1. gravitation,
2. electromagnetism,
3. the weak nuclear force,
4. and the strong nuclear force.

While attosecond-level physics can describe all gravitational and electromagnetic interactions, they can only explain and probe most of the weak interactions, not all of them, and can’t explain any of the interactions that are mediated by the strong nuclear force. Attoseconds aren’t fast enough for all of particle physics; if we truly want to understand the Universe, we’ll have to get down to yoctosecond (~10^-24 second) precision. Here’s the science, and the inherent limitations, of that endeavor.

On the right, the gauge bosons, which mediate the three fundamental quantum forces of our Universe, are illustrated. There is only one photon to mediate the electromagnetic force, there are three bosons mediating the weak force, and eight mediating the strong force. This suggests that the Standard Model is a combination of three groups: U(1), SU(2), and SU(3), whose interactions and particles combine to make up everything known in existence. Despite the success of this picture, many puzzles still remain.

The speed of light is your friend

For most purposes used here on Earth, the speed of light is fast enough to be considered instantaneous. The first recorded, scientific attempt to measure the speed of light was performed by Galileo, who — in true Lord of the Rings/Beacons of Gondor fashion — sent two people with lanterns up to the peaks of mountains, where one mountaintop could be seen from the summit of the other. The experiment would proceed as follows:

• Mountaineer #1 and Mountaineer #2 would each be equipped with a lantern, which they could unveil at any moment.
• Mountaineer #1 would unveil their lantern first, and upon seeing the light from it, Mountaineer #2 would then unveil their own lantern.
• And then, assuming there was a time-delay, Mountaineer #1 would be able to record the amount of time it took from when they unveiled their lantern to when they saw the light from Mountaineer #2’s lantern.

Unfortunately, upon performing this experiment, Galileo could only conclude that the speed of light was very, very fast: indistinguishable from instantaneous compared to the reaction time of a human being. It’s only when tremendous distances are at play — such as when we communicated with astronauts on the Moon during the Apollo era — that the speed of light, at roughly 300,000 km/s (186,000 mi/s) causes an appreciable delay in the arrival-time of a signal.

The Lunar Laser Ranging Experiment apparatus was first installed on the Moon as part of the Apollo 11 mission, and that plus other Apollo-era lunar retroreflectors are still used today by astronomers seeking to measure the Earth-Moon distance to the greatest precision possible. At its average distance of 380,000 km from Earth, the round-trip light-travel time from the Earth to the Moon and back is about 2.5 seconds: the approximate time delay between mission control and the Apollo astronauts who landed on the Moon.

But in the era of precision particle physics, this is not a bug, but rather a tremendous feature! One of the classic ways of studying particles is to collide them together at incredibly high speeds — speeds that are extremely close to and often practically indistinguishable from the speed of light — and to track the debris that comes out of those collisions with whatever sufficiently-advanced techniques are available at your disposal.

Over time, those techniques have evolved, from early cloud chambers to later bubble chambers to more modern silicon and pixel detectors, allowing us to both get close to and stand at great distances from the collision point, reconstructing what occurred at each point along the way.

This is an excellent case of where the speed of light is a tremendous asset, particularly if the particles produced from your collision are relativistic (i.e., close to the speed of light) relative to the rest-frame of your detector. In these instances, one of the most important things you can see is what’s known as a “displaced vertex,” as it shows where you had an “invisible” particle (that doesn’t show up in your detector) decay into visible ones that leave tracks behind.

Bubble chamber tracks from Fermilab, revealing the charge, mass, energy, and momentum of the particles and antiparticles created. This recreates similar conditions to what was present during the Big Bang, where matter and antimatter can both be readily created from pure energy. At the highest energies, all particles and antiparticles can be created, but at energies corresponding to “only” a temperature of ~10 billion K or so, electron-positron pairs can still be spontaneously created.

In other words, the speed of light gives us a way to convert “time” into “distance” and vice versa. Consider the following for a particle that moves extremely close to the speed of light.

• If it travels for 1 second (1.00 seconds), it travels a distance of up to 300,000 km.
• If it travels for 1 microsecond (10^-6 seconds), it travels up to 300 meters.
• If it travels for 1 picosecond (10^-12 seconds), it travels up to 0.3 millimeters, or 300 microns.
• If it travels for 1 attosecond (10^-18 seconds), it travels up to 0.3 nanometers, or 3 angstroms.
• And if it travels for 1 yoctosecond (10^-24 seconds), it travels up to 0.3 femtometers, or 3 × 10^-15 meters.

From the perspective of a human being, nanosecond-level precision would be enough to tell the difference between a light-signal that interacted with one human versus another, as ~30 centimeter precision can normally distinguish one human from the next.

From the perspective of an atom or molecule, attosecond-level precision is sufficient, and that’s why this year’s Nobel Prize in physics is such a big deal; you can tell whether a water molecule is in a liquid or gaseous state with attosecond-level timing accuracy.

By applying the technique of attosecond spectroscopy, it was found that photoemission from liquid water electrons shows a time delay of 50-70 attoseconds compared with photoemission from the gaseous (water vapor) phase. This research was enabled by the pioneering work of Pierre Agostini, Ferenc Krausz and Anne L’Huillier: 2023’s Nobel Laureates in physics.

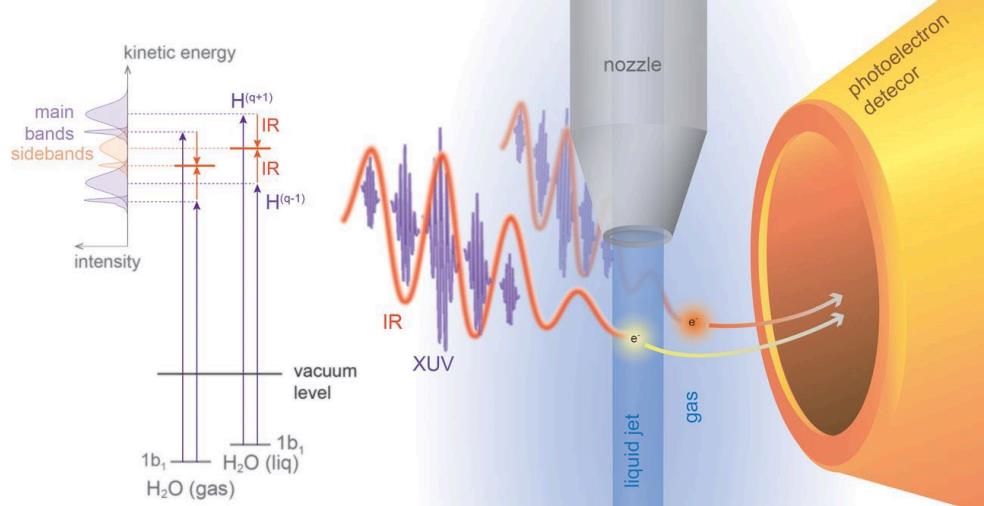
What about for particles?

This is where things get tricky. If all you want to do is distinguish one particle from another, then measuring your location down to a precision that’s smaller than the separation distances between the particles is sufficient. If your particles are atom-sized (about an angstrom), then attosecond timing will do it. If your particles are atomic-nucleus sized (about a femtometer), then you need yoctosecond timing.

But in reality, this is not how we measure or tag individual subatomic particles. We don’t typically have a system of distinct particles where we want to know which one we’re interacting with; instead, we have:

• a collision point,
• that produces a series of particles and/or antiparticles,
• some of which are neutral and some of which are charged,
• some of which are stable and some of which are unstable,
• and some of which interact with various media and some of which do not.

So, what we do is set up a variety of conditions around the collision point — a point which we, the experiment-makers, control — to try and coax these particles into interacting. We can set up easily electrified media, so that when charged and/or fast-moving particles pass through them, they create an electric current. We can set up easily ionized media, so that when a photon of a high-enough energy strikes it, it produces an “avalanche” of electric current.

A candidate Higgs event in the ATLAS detector at the Large Hadron Collider at CERN. Note how even with the clear signatures and transverse tracks, there is a shower of other particles; this is due to the fact that protons are composite particles, and due to the fact that dozens of proton-proton collisions occur with every bunch crossing. At higher energies, discoveries that don’t appear at lower energies become possible. Modern particle detectors are like a layer-cake, with the ability to track the particle debris in order to reconstruct what happened as close to the collision point as possible.

We can also set up magnetic fields, which bend charged particles dependent on their speed and charge-to-mass ratios, but that leave neutral particles alone. We can set up dense media that possess lots of “stopping power” for slowing down fast-moving, massive particles. And so on and so forth, where each piece of information, compounded atop the last, can help reveal the properties of the “daughter particles” produced by the reaction, giving us the ability to reconstruct what happened as close to the collision point as possible.

But even so, there are limits.

If you make a particle that decays via the weak interactions, with typical lifetimes that range from ~10^-10 seconds (for Lambda baryons) to ~10^-8 seconds (for kaons and charged pions) to ~10^-6 seconds (for muons), you can usually see the “displaced vertex” and measure the time-of-flight directly, as such a particle will travel millimeters or more before decaying.

If you make a particle that decays via the electromagnetic interactions, with the neutral pion being the classic example but of the eta meson also decaying via this pathway, its typical lifetime will be between ~10^-17 seconds up to ~10^-19 or ~10^-20 seconds, which is perilously fast: too fast to measure directly in a detector.

The decays of the positively and negatively charged pions, shown here, occur in two stages. First, the quark/antiquark combination exchanges a W boson, producing a muon (or antimuon) and a mu-neutrino (or antineutrino), and then the muon (or antimuon) decays through a W-boson again, producing a neutrino, an antineutrino, and either an electron or positron at the end. This is the key step in making the neutrinos for a neutrino beamline, and requires two separate decays through the weak interaction: first of the pion into a muon, and then of a muon into an electron. The W+ and W- bosons are one another’s antiparticle, but the Z0 is its own antiparticle.

You might think we’re close; if we’re at just about the attosecond level in our precision, then perhaps we can start measuring particle positions with either faster pulses or by positioning our detectors even closer to the collision point.

But detector positioning won’t help, because detectors are made out of atoms, and so there’s a limit to how close you can position your detector to the collision point that will give you meaningful time differences: attosecond-scales are just about it.

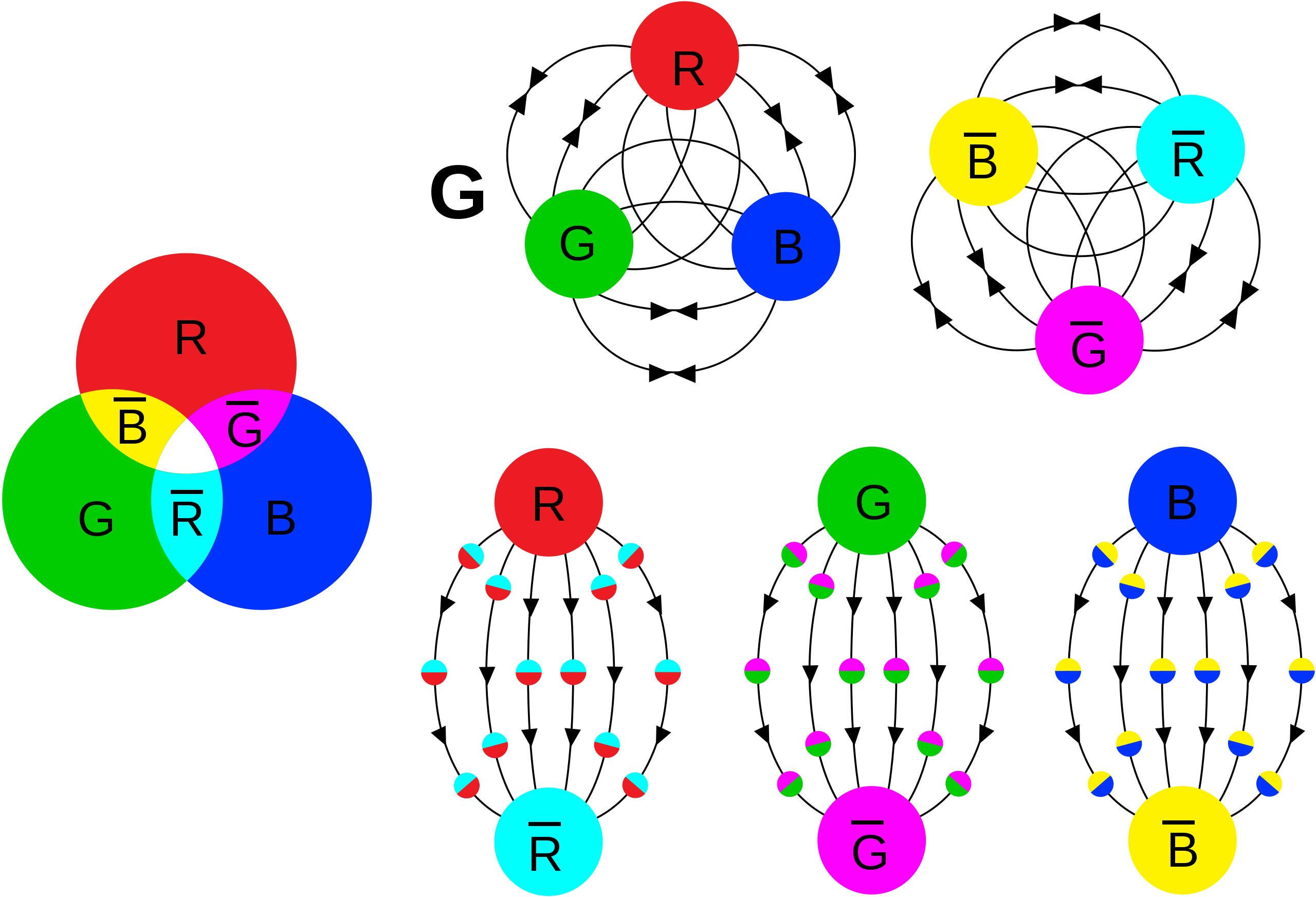
And besides, there are two other factors that come into play that render hand-wringing about electromagnetic decays all but moot: the strong interactions and the Heisenberg uncertainty principle. It’s important to remember that most of the composite particles that we create in particle accelerators — baryons, mesons, and anti-baryons — are made out of quarks, and quarks have this property that there are no such things are free quarks in nature: they must exist in bound, colorless states, which requires either:

• three quarks,
• three antiquarks,
• a quark-antiquark pair,
• or combinations of two or more of these stacked upon one another,

in order to exist.

Combinations of three quarks (RGB) or three antiquarks (CMY) are colorless, as are appropriate combinations of quark/antiquark pairs. The gluon exchanges that keep these entities stable are quite complicated, but require eight, not nine, gluons. Particles with a net color charge are forbidden under the strong interactions.

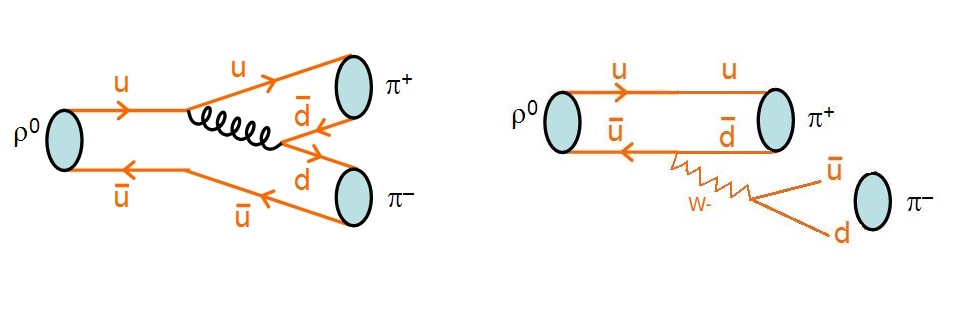
This means that, every time a particle experiment shoots off either a single quark or antiquark with a lot of energy in one direction, it won’t exist as a “solo particle” for any detectable length of time. Instead, it will undergo a process called hadronization, where quark-antiquark pairs are ripped out of the quantum vacuum until only bound, color-neutral states are produced. In particle physics experiments, this inevitably looks like “jets” of particles made out of quarks (and antiquarks) are produced. Although jets are usually mostly composed of various types of pions, all types of particles involving all types of quarks can be produced, particularly if enough energy is available. As far as we can measure, this “hadronization” occurs instantly.

So then we come to the third type of decay: a strong decay. Particles like the Delta baryons are made up of up-and-down quarks, just like a proton or neutron, but have a rest-mass of 1,232 MeV/c², meaning that it’s energetically favorable for them to decay into either proton + pion or neutron + pion combinations, rather than remain as a Delta baryon. Because of this, there are no weak or electromagnetic processes that need to occur; only the strong interaction is required. And for the strong interaction, only ~10^-24 seconds are required for a decay: yoctosecond level timescales.

In theory, the rho meson could either decay to a pair of pions by the strong interaction (left) or the weak interaction (right). Because of the relative strength of these interactions and the high mass of the W-boson, the strong decay channel is the only one that’s relevant for our experiments, and the rho decays in ~10^-24 seconds in practice.

A yoctosecond is a million times faster than an attosecond; you cannot hope to measure it with a conventional detector. But what’s even more bonkers is if we look at the most massive fundamental particles of all:

• the W-and-Z bosons,
• the Higgs boson,
• and the top quark.

With masses between 80 and 173 GeV/c², their lifetimes are an impressively tiny ~10^-25 seconds: the shortest-lived particles known.

Because their masses are so large, they can, in theory, decay via any pathway that conserves all the necessary quantum properties of particles: baryon number, lepton number, charge, spin, energy, momentum, etc. The top quark, interestingly enough, can only decay through the weak interaction, but has a mean lifetime that’s so short (~5×10⁻²⁵ s) that it cannot hadronize; it simply decays away.

All of these particles are so short-lived that when you produce one, their lifetime (Δt) is so short, that from the Heisenberg uncertainty relation (ΔEΔt ≥ ħ/2) combined with Einstein’s E = mc², ensures that they will have varying masses from one particle of the same species to the next. You can only measure the average mass by collecting large numbers of particles; the mass of any individual such particle will have what we call an inherent width to it.

The inherent width, or half the width of the peak in the above image when you’re halfway to the crest of the peak, is measured to be 2.5 GeV: an inherent uncertainty of about +/- 3% of the total mass. The mass of the particle in question, the Z boson, is peaked at 91.187 GeV, but that mass is inherently uncertain by a significant amount owing to its excessively short lifetime. This result is remarkably consistent with Standard Model predictions.

Particles that decay through the strong interactions cannot be detected with conventional particle detectors; you can only detect them indirectly: as resonances that appear in certain experiments. The top quark and the Higgs boson have only been detected indirectly as well: as excess events that show up at certain energies over and above the known contributions from other sources and backgrounds. If we ever wanted to try and probe these particles directly, it would require going far beyond the limits of attosecond-scale physics; we’d have to improve by a factor of more than a million, getting down to yoctosecond, or ~10^-24 second, timescales, and probing subatomic distances that are around ~10^-17 meters or smaller: about 100 times smaller than the width of a proton.

It’s resulted in a very strange way of thinking about the Universe: particles that “only” decay via the weak interactions, and that live for only a few picoseconds to a few nanoseconds in duration, are now considered “stable” compared to particles that decay via the strong interaction. That many particles don’t live long enough to obey the “rules” that should bind all subatomic particles. And that particles that live for short enough amounts of time don’t even have definitive properties like mass, instead existing only in an indeterminate state due to the quantum bizarreness of nature. As far as we’ve come in our understanding of the Universe, getting down to attosecond timescales simply isn’t good enough to account for particle physics and all that it includes.