Ask Ethan: Where does quantum uncertainty come from?

- No matter how you attempt to measure or calculate certain quantum properties, there will always be some inherent uncertainty present, making complete knowledge of such a system impossible.
- But where does that uncertainty come from? Is it a property inherent to particles, or is there some other underlying cause that we haven't yet been able to uncover?
- Could it have anything to do with the quantum fields that are inherent to empty space itself? Or does that just punt the known problem into unknown territory?
Perhaps the most bizarre property we’ve discovered about the Universe is that our physical reality doesn’t seem to be governed by purely deterministic laws. Instead, at a fundamental, quantum level, the laws of physics are only probabilistic: you can compute the likelihood of the possible experimental outcomes that will occur, but only by measuring the quantity in question can you truly determine what your particular system is doing at that instant in time. Furthermore, the very act of measuring/observing certain quantities leads to an increased uncertainty in certain related properties: what physicists call conjugate variables.
While many have put forth the idea that this uncertainty and indeterminism might only be apparent, and could be due to some unseen “hidden” variables that truly are deterministic, we have yet to find a mechanism that allows us to successfully predict any quantum outcomes. But could the quantum fields inherent to space be the ultimate culprit? That’s this week’s question from Paul Marinaccio, who wants to know:
“I’ve been wondering for a long time: does the quantum vacuum supply the whatever for the particle wave packet vibrations. Does it act… the way people thought the ether did? I know this is a vastly simplified way of asking the question but I don’t know how to put it in mathematical terms.”
Let’s take a look at what the Universe has to say about such an idea. Here we go!

In quantum physics, there are two main ways to think about uncertainty. One is, “I created my system with these particular properties, and then when I come back at some later time, what can I say about those properties?” For some properties — like the mass of a stable particle, the electric charge of a particle, the energy level of an electron bound in its atom’s ground state, etc. — those properties will remain unchanged. As long as there are no further interactions between the quantum particle and its environmental surroundings, these properties will fall clearly into the realm of the known, with no uncertainty.
But other properties are less certain. Put down a free electron in space at a precisely known position, and when you come back later, the electron’s position can no longer be definitively known: the wavefunction that describes its position spreads out over time. If you want to know whether an unstable particle has decayed, you can only find out by measuring that particle’s properties and seeing whether it has or not. And if you ask what the mass of an unstable particle that radioactively decayed was, which you can reconstruct by measuring the energy and momentum of each of the particles it decayed into, you’ll get a slightly different answer from event-to-event, uncertain dependent on the particle’s lifetime.
That’s a form of uncertainty that arises because of time-evolution: because the quantum nature of reality ensures that certain properties can only ever be known to a certain precision. As time goes on, that uncertainty propagates into the future, leading to a physical state that cannot be arbitrarily well-known.
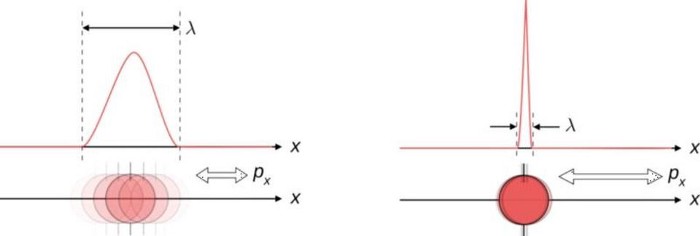
But there’s another way that uncertainty arises: because certain pairs of quantities — those conjugate variables — are related in ways where knowing one to better precision inherently reduces the knowledge you can possess about the other one. This arises directly from the Heisenberg uncertainty principle, and it rears its head in a wide variety of situations.
The most common example is between position and momentum. The better you measure where a particle is, the less inherently able you are to know what its momentum is: how fast and in what direction its “quantity of motion” is. This makes sense if you think about how a measurement of position is made: by causing a quantum interaction between the particle you’re measuring with another quantum, either with or without a rest mass. Either way, the particle can be assigned a wavelength, with more energetic particles having shorter wavelengths, and hence being able to measure a position more precisely.

But if you stimulate a quantum particle by causing it to interact with another quantum particle, there’s going to be an exchange of momentum between them. The greater the energy of the interacting particle:
- the shorter its wavelength is,
- leading to a better-known position,
- but also leading to a greater amount of energy-and-momentum imparted to the particle,
- which leads to a greater uncertainty in its momentum.
You might think you can do something clever to “cheat” this, such as measuring the momentum of the outgoing particle that you used to determine the particle’s position, but alas, such an attempt doesn’t save you.
There’s a minimum amount of uncertainty that’s always preserved: the product of your uncertainty in each of the two quantities must always be greater than or equal to a specific value. No matter how well you measure the position (Δx) and/or momentum (Δp) of each particle involved in these interactions, the product of their uncertainty (ΔxΔp) is always greater than or equal to half of the reduced Planck constant, ħ/2.
There are many other quantities that exhibit this uncertainty relation, not just position and momentum. These include:
- orientation and angular momentum,
- energy and time,
- a particle’s spin in mutually perpendicular directions,
- electric potential and free electric charge,
- magnetic potential and free electric current,
It’s true that we live in a quantum Universe, so it makes sense, intuitively, to ask whether there isn’t some sort of hidden variable underpinning all of this quantum “weirdness.” After all, many have philosophized over whether these quantum notions that this uncertainty is unavoidable is inherent, meaning that it’s an inextricable property of nature itself, or whether there’s an underlying cause that we simply haven’t been able to pinpoint. The latter approach, favored by many great minds throughout history (including Einstein), is commonly known as a hidden variables assumption.

The way I like to imagine hidden variables is like having the Universe, and all the particles in it, sitting atop a rapidly, chaotically vibrating plate set to the lowest amplitude setting. When you’re looking at the Universe on large, macroscopic scales, you can’t see the effects of this vibration at all; it appears as though the “backdrop” of the Universe that all the particles exist in is stable, constant, and devoid of fluctuations.
But as you look down to smaller and smaller scales, you notice that there are these quantum properties present. Quantities do fluctuate; things don’t remain perfectly stable and unchanging over time; and the more persistently you try to pin down any one particular quantum property, the greater you’ll find an uncertainty in its associated conjugate quantity.
You can easily imagine, based on the fact that there are quantum fields permeating all of space, even completely empty space, that these underlying fields themselves are the source of all of it. The uncertainty that we’re seeing, perhaps, arises as a consequence of the quantum vacuum.

It’s definitely not an idea that’s easy to rule out, given that the fact of quantum uncertainty is “baked in” to our fundamental understanding of particles and fields. Every formulation (that works) of quantum mechanics and quantum field theory includes it, and includes it at a fundamental level, not just as an ad hoc addition after-the-fact. In fact, we don’t even know how to use quantum field theory to calculate what the overall contribution to the quantum vacuum is for each of the fundamental forces; we only know, through our measurement of dark energy, what the total contribution must be. When we attempt to do such a calculation, the answers we get are nonsensical, providing us with no meaningful information at all.
But there are a few pieces of information that would be difficult to explain with the idea that fluctuations in the underlying space itself is responsible for the quantum uncertainty and wave-packet spreading that we observe. For one, just consider what happens when you take a quantum particle that has an inherent (spin) angular momentum, you allow it to move through space, and you apply a magnetic field to it.
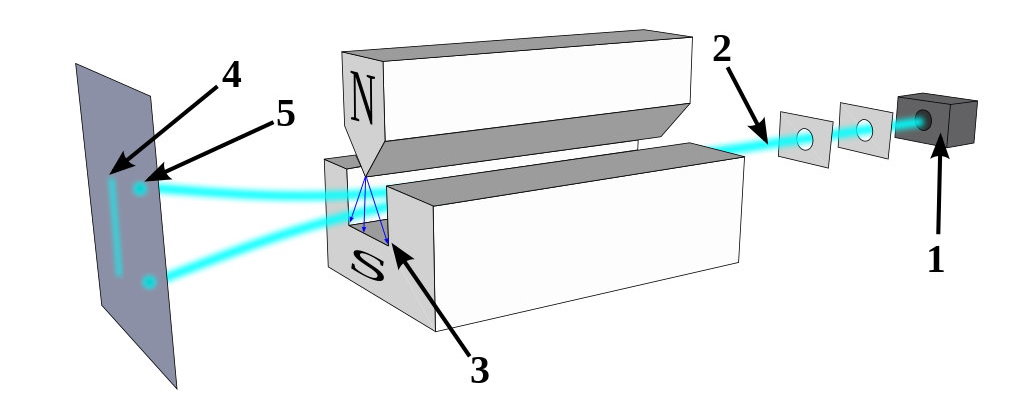
That particle will deflect by either a positive or negative amount: dependent on the direction of the magnetic field you apply to it and on whether the spin of that particle happens to be oriented in the positive or negative direction. The deflection occurs along the same dimension that the magnetic field is applied in.
Now go and apply a magnetic field in a different, perpendicular direction. You’ve already determined what the spin was in one particular direction, so what do you think will happen if you apply that magnetic field in a different direction?
The answer is that the particle will deflect again, with a 50/50 probability of either being aligned with the direction of the field or being anti-aligned with the direction of the field.
But that’s not the interesting part. The interesting part is that the act of making that measurement, of applying that extra, perpendicular field, actually destroyed the information you had previously gained from applying that first magnetic field. If you then apply the identical field that you applied back during the first part of the experiment, those particles, even if they were all positively oriented previously, will have random spins once again: 50/50 aligned versus anti-aligned with the field.
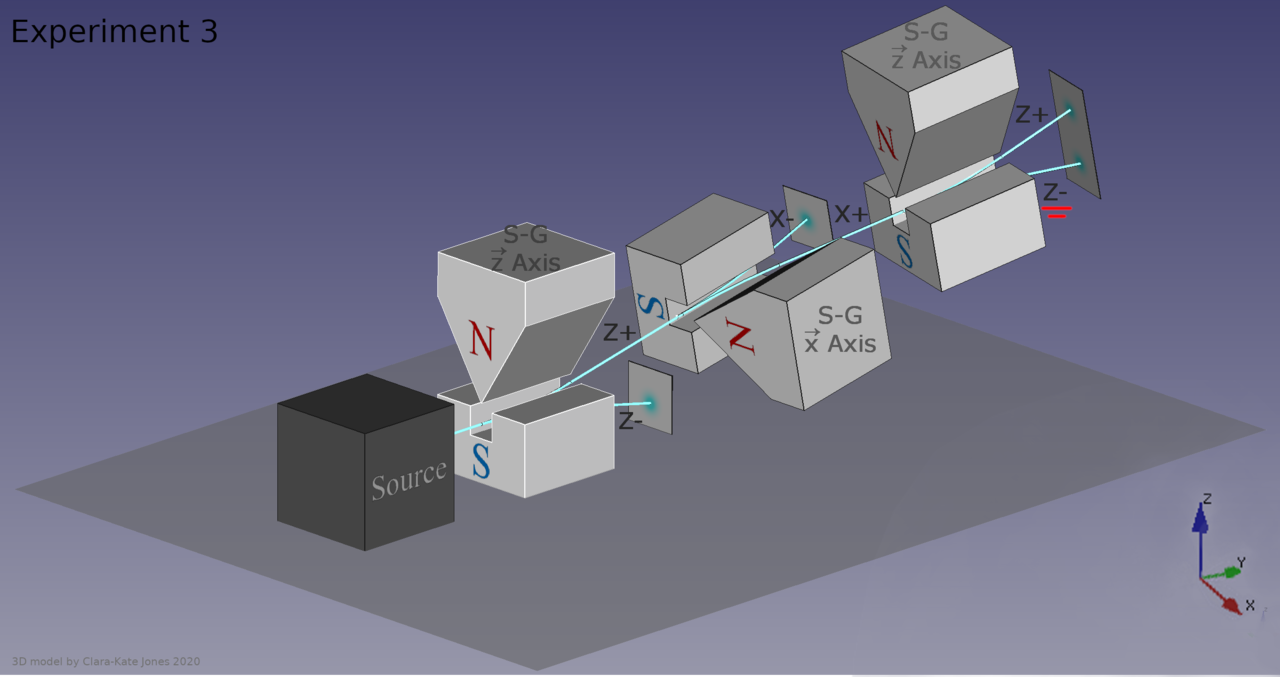
It’s very hard to make sense of this under the assumption that the quantum vacuum itself is responsible for the whole of quantum uncertainty. In this instance, the particle’s behavior is dependent on the external field you applied to it and the subsequent interactions that it experienced, not on the properties of the empty space that it passed through. If you remove the second magnet from the aforementioned setup — the one that was oriented perpendicular to the first-and-third magnets — there would be no uncertainty as to the particle’s spin by the time it made it to the third magnet.
It’s hard to see how “empty space” itself, or “the quantum vacuum” if you prefer, could be responsible for quantum uncertainty based on what the results of this experiment show. It’s the interactions (or lack thereof) that a quantum system experiences which dictate how quantum uncertainty rears its head, not any property inherent to the fields permeating all of space.
Like it or not, the reality of what you observe depends on how and whether you observe it; you simply get different experimental outcomes owing to the specifics of your measurement apparatus.
To date, there is no theory of hidden variables that has resulted in any experimental or observational evidence that there is an underlying, objective reality that’s independent of our measurements. Many people suspect that this is true, but this is based on intuition and philosophical reasoning: neither of which are admissible as scientifically valid reasons for drawing a conclusion of any sort.
That doesn’t mean people shouldn’t keep formulating such theories or attempting to design experiments that could reveal or rule out the presence of hidden variables; that’s part of how science moves forward. But so far, all such formulations have only led to constraints on and invalidations of specific classes of hidden variable theories. The notion that there are “hidden variables, and they’re all encoded in the quantum vacuum,” cannot be ruled out.
But if I were to bet on where to look next, I’d note that in the (Newtonian) theory of gravity, there are also conjugate variables present: gravitational potential and mass density. If the analogy with electromagnetism (between electric potential and free electric charge) holds, which we expect it to, that means we can extract an uncertainty relation for gravity as well.
Is gravitation an inherently quantum force? Someday, we might be able to experimentally determine whether this quantum uncertainty exists for gravitation as well. If so, we’ll have our answer.
Send in your Ask Ethan questions to startswithabang at gmail dot com!