How quantum uncertainty saved the atom

The 19th and early 20th centuries were both the best of times and the worst of times for the building block of all the matter on Earth: the atom. In 1803, John Dalton put forth what we now know as modern atomic theory: the postulate that everything is made of indivisible atoms, where every atom of the same species is identical and possesses the same properties as all other atoms of that type. When atoms are combined into chemical compounds, the possibilities become virtually endless, while different atoms themselves could be sorted into classes with similar properties based on the periodic table scheme of Dmitri Mendeleev.

But two experiments — with cathode ray tubes in 1897 and with radioactive particles in 1911 — demonstrated that atoms were actually composed of positively-charged, massive atomic nuclei and negatively-charged, light electrons, which instantly created a paradox. If this is what atoms were made of, then the laws of electricity and magnetism demanded that atoms would be unstable, collapsing in on themselves in only a fraction of a second. Yet atoms are observed to not only be stable, but to compose all of our tangible reality.

How, then, does physics wind up saving the atom from this catastrophic fate? The simple answer lies in the Heisenberg uncertainty principle, which not only saved the atom, but allowed us to predict their sizes. Here’s the science of how.

The periodic table of the elements is sorted as it is (in row-like periods and column-like groups) because of the number of free/occupied valence electrons, which is the number one factor in determining each atom’s chemical properties. Atoms can link up to form molecules in tremendous varieties, but it’s the electron structure of each one that primarily determines what configurations are possible, likely, and energetically favorable.

The idea of the atom goes all the way back to Ancient Greece, and the musings of an intellectual figure named Democritus of Abdera. A strong believer in a materialist viewpoint of the world — that all of our experience could be explained by the physical components of reality — Democritus rejected the notion of purposeful and divine influences on the world, and instead became the founder of atomism. What appeared to us as the order and regularity of the world, according to his ideas, were because there were only a finite number of “building blocks” that reality was assembled out of, and that these building blocks, those indivisible atoms, were the only materials needed to build up and compose all that we knew.

Experiments in the 18th century involving combustion, oxidation, and reduction led to the disproof of many alternate theories of the material Universe, while Dalton and Mendeleev described and sorted the atomic building blocks of our reality by similar physical, chemical, and bonding properties. For a time, it seemed as if we were well on our way to a complete description of reality: as being composed of atoms, which in turn built up everything else.

But it wasn’t to be, as in 1897, J.J. Thomson demonstrated that atoms themselves were not indivisible, but instead had “parts” to them. His experiments with what were then known as “cathode rays” swiftly revolutionized how we thought about the nature of matter.

The traditional model of an atom, now more than 100 years old, is of a positively charged nucleus orbited by negatively charged electrons. Although the outdated Bohr model is where this picture comes from, we can arrive at a better one simply by considering quantum uncertainty.

The existence of electric charge was already known, and the relationship between charged particles and both electric and magnetic fields were uncovered previously in the 19th century: by Ampere, Faraday, and Maxwell, among others. When Thomson came along, he set out to discover the nature of cathode rays.

• When he fired cathode rays at an electroscope, they charged it up, demonstrating that the particles they fired off were, in fact, “electrified” in some sense.
• He then showed that these particles could be bent by a magnet, and that the way (direction) they were bent showed that they carried a negative electric charge.
• And finally, he took a prior experiment that had been performed by Heinrich Hertz, which showed that cathode rays were not deflected by an electric field, and improved it. In Hertz’s experiment, cathode rays were fired into an electric field, which should deflect charged particles, but no deflection was seen. Thomson reasoned that the gas through which the cathode rays were traveling played a role, and by removing the gas (creating a vacuum), showed that the expected deflection did indeed occur.

Matter, in other words, wasn’t just made of atoms, but atoms themselves contained these negatively charged, very low-mass constituents, which are today known as electrons, inside of them.

In combination with the discovery of radioactivity — where certain types of atoms were shown to spontaneously emit particles — it was looking more and more like atoms themselves were actually made of smaller constituents: some type of “subatomic” particle must exist inside of them.

When cathode rays (blue, at left) are emitted and passed through a hole, they propagate through the remainder of the apparatus. If an electric field is applied and the apparatus has the air inside removed, the cathode particles will deflect downward, consistent with the notion that they are light, negatively charged particles: i.e., electrons.

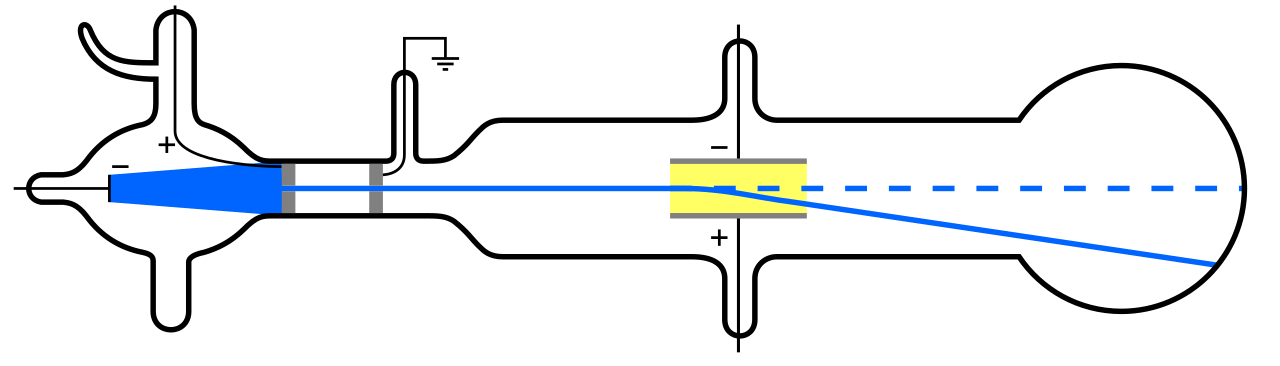
But since atoms are electrically neutral and quite massive, rather than “light” like the electron, there must be some other type of particle inside an atom as well. It wasn’t until 1911 that the experiments of Ernest Rutherford came to pass, which would investigate the nature of these “other” particles inside the atom as well.

What Rutherford did was simple and straightforward. The experiment began with a ring-shaped apparatus designed to detect particles encountering it from any direction. In the center of the ring, thinly hammered gold foil was placed of a thickness so small it couldn’t be measured with early-20th century tools: likely just a few hundred or thousand atoms across.

Outside of both the ring and the foil, a radioactive source was placed, so that it would bombard the gold foil from one particular direction. The expectation was that the emitted radioactive particles would see the gold foil much the way a charging elephant would see a piece of tissue paper: they’d simply go right through as though the foil weren’t there at all.

Rutherford’s gold foil experiment showed that the atom was mostly empty space, but that there was a concentration of mass at one point that was far greater than the mass of an alpha particle: the atomic nucleus.

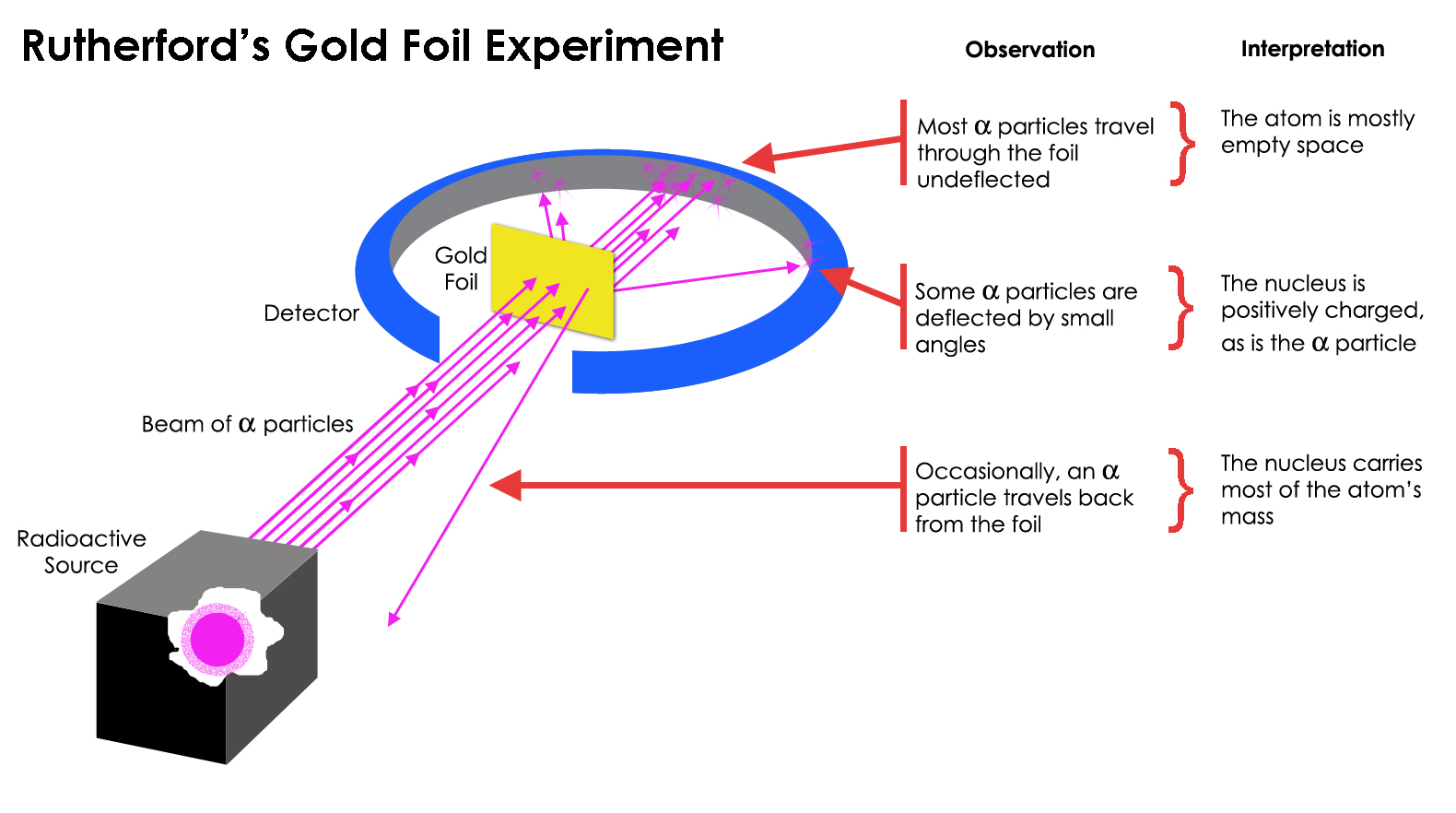
But this turned out only to be true for most of the radioactive particles, not all of them. A few of them — small in number but vitally important — behaved as though they bounced off of something hard and immovable. Some of them scattered off to one side or the other, while others appeared to ricochet back toward their direction of origin. This early experiment provided the very first evidence that the inside of an atom wasn’t a solid structure as previously envisioned, but rather consisted of an extremely dense, small core and a much more diffuse outer structure. As Rutherford himself remarked, looking back decades later,

“It was quite the most incredible event that has ever happened to me in my life. It was almost as incredible as if you fired a 15-inch shell at a piece of tissue paper and it came back and hit you.”

This type of experiment, where you fire a low, medium, or high-energy particle at a composite particle, is known as deep inelastic scattering, and it remains our best method for probing the internal structure of any system of particles.

If atoms had been made of continuous structures, then all the particles fired at a thin sheet of gold would be expected to pass right through it. The fact that hard recoils were seen quite frequently, even causing some particles to bounce back from their original direction, helped illustrate that there was a hard, dense nucleus inherent to each atom.

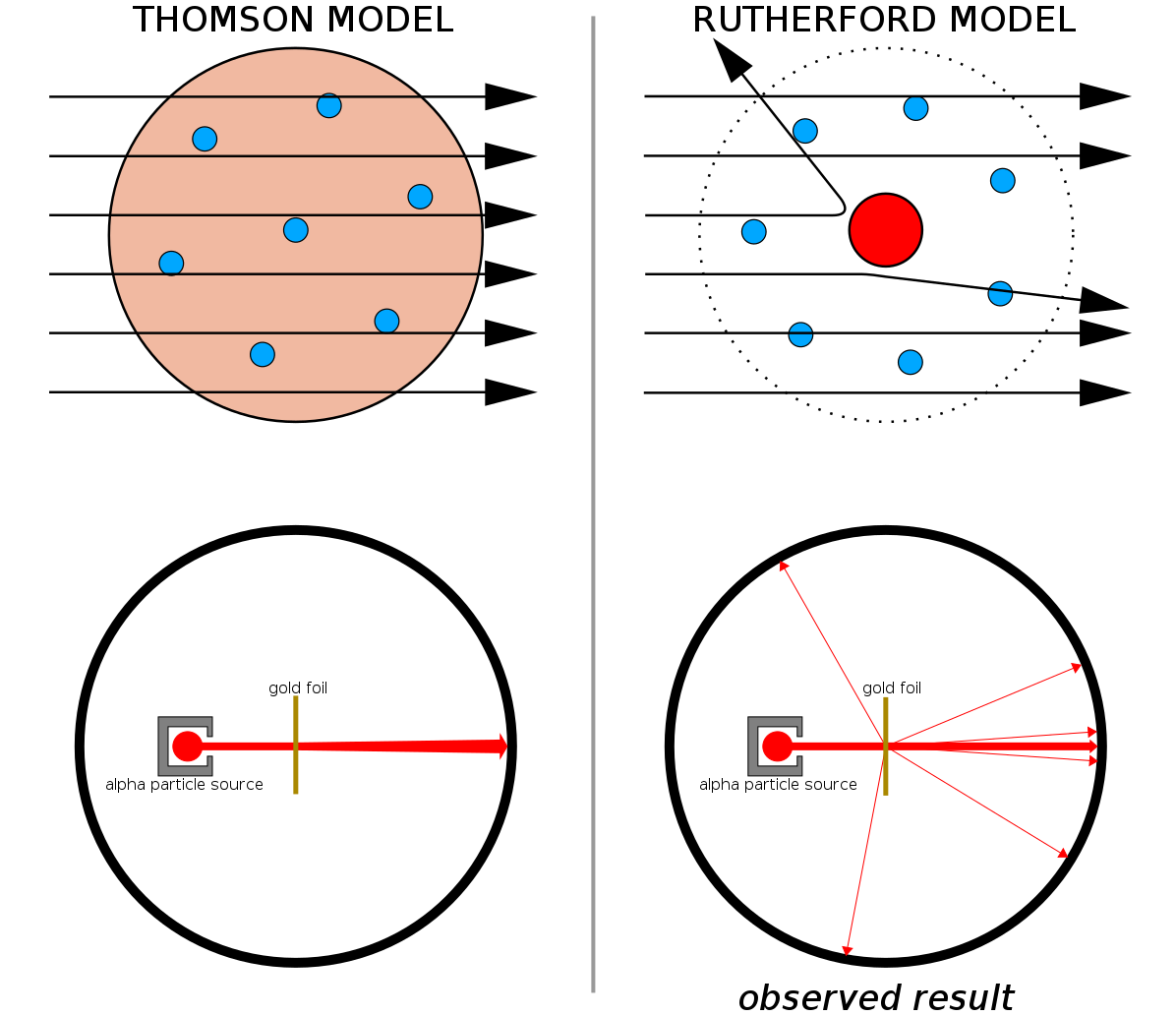
Combined with Thomson’s earlier work (and notably, Rutherford was a former student of Thomson’s), we now had a model for an atom that consisted of:

• a massive, small, positively charged atomic nucleus,
• surrounded by a series of very low-mass, even smaller, negatively charged electrons.

Rutherford, as one might be tempted to do, then went on to construct a model of the atom: a Solar System-like one, where the negatively-charged electrons orbited around the positively-charged nucleus, just like the planets of the Solar System orbited around the Sun.

But this model was fatally flawed, and even Rutherford realized it right away. Here’s the problem: electrons are negatively charged, while the atomic nucleus is positively charged. When a charged particle sees another charged particle, it accelerates, owing to the electric force acting on it. But accelerating charged particles radiate electromagnetic waves — i.e., light — causing them to lose energy. If electrons were orbiting a nucleus, they should radiate energy away, causing their orbits to decay, which in turn should cause them to spiral into the nucleus. Simply by using the equations of classical electromagnetism, Rutherford showed that his model was unstable (on timescales of less than a second), so the stability of the atom clearly meant that something else was at play.

In the Rutherford model of the atom, electrons orbited the positively charged nucleus, but would emit electromagnetic radiation and see that orbit decay. It required the development of quantum mechanics, and the improvements of the Bohr model, to make sense of this apparent paradox.

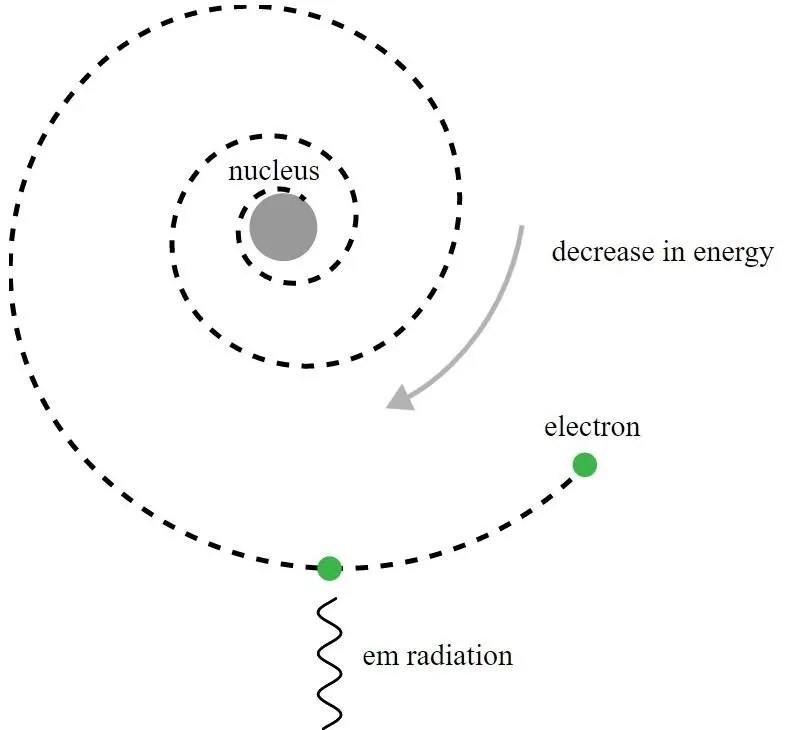
Although, historically, it was Niels Bohr whose primitive quantum mechanical model would lead to a new theory for the atom and the idea that atoms had energy levels which were quantized, Bohr’s model itself is incomplete and ad hoc in many ways. A more fundamental principle of quantum mechanics — one that was not yet known to Rutherford’s contemporaries in 1911 — actually holds the powerful key to explaining why atoms are stable: the Heisenberg uncertainty principle.

Although it wasn’t discovered until the 1920s, the Heisenberg uncertainty principle tells us that there’s always an inherent uncertainty between what are known as “complementary quantities” in physics. The more accurately you measure/know one of these quantities, the more inherently uncertain the other one gets. Examples of these complementary quantities include:

• energy and time,
• position and momentum,
• orientation and angular momentum,
• inherent spin in mutually perpendicular directions,
• voltage and free electric charge,
• electric field and electric polarization density,

plus many others. The most famous example, and the one that applies here, is the position-momentum uncertainty relation.

This diagram illustrates the inherent uncertainty relation between position and momentum. When one is known more accurately, the other is inherently less able to be known accurately. Other pairs of conjugate variables, including energy and time, spin in two perpendicular directions, or angular position and angular momentum, also exhibit this same uncertainty relation.

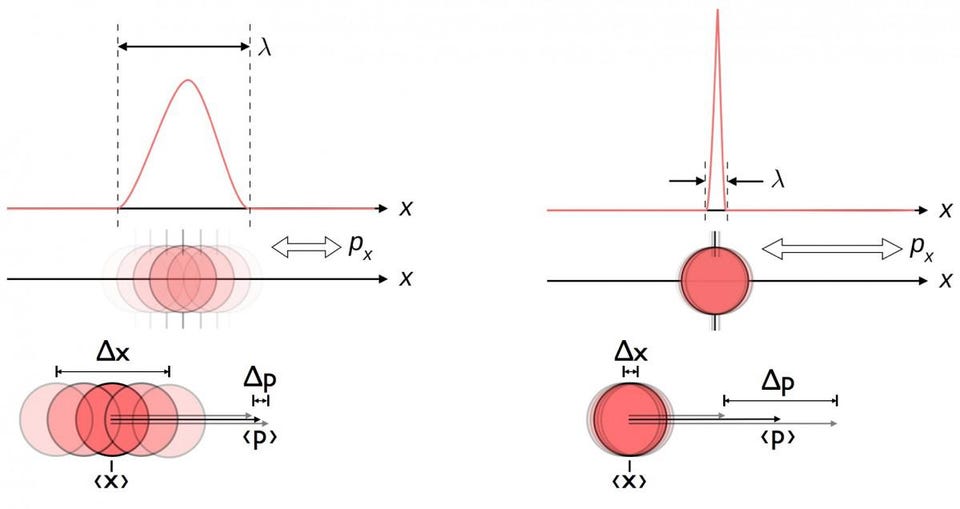
No matter how well you measure the position (Δx) and/or momentum (Δp) of each particle involved in any physical interaction, the product of their uncertainty (ΔxΔp) is always greater than or equal to half of the reduced Planck constant, ħ/2. And remarkably, just by using this uncertainty relation, along with the knowledge that atoms are made of (heavy) positively charged nuclei and (light) negatively charged electrons, you can derive not only the stability of an atom, but the physical size of an atom as well!

Travel the Universe with astrophysicist Ethan Siegel. Subscribers will get the newsletter every Saturday. All aboard!

Here’s how.

The simplest law in all of electromagnetism is Coulomb’s law, which tells you the electric force between two charged particles. In direct analogy to Newton’s law of universal gravitation, it tells you that the force between those particles is some constant, multiplied by each of the charges of the two particles involved, divided by the distance squared between them. And again, in direct analogy to Newton’s gravity, you can also derive from that related quantities like:

• the strength of the electric field (or the strength of the gravitational field),
• the instantaneous acceleration of a charged (or massive) particle in that field,
• and the electric (or gravitational) potential energy of a particle in this system’s vicinity.

Newton’s law of universal gravitation (left) and Coulomb’s law for electrostatics (right) have almost identical forms, but the fundamental difference of one type vs. two types of charge open up a world of new possibilities for electromagnetism. In both instances, however, only one force-carrying particle, the graviton or the photon, respectively, is required.

We’re going to figure this out for the simplest case of all atoms: the hydrogen atom, whose atomic nucleus is just a single proton. So let’s take three equations — for those of you hoping there would be no math, I apologize for the rest of this brief section — and let’s do what we can to put them together. The three equations, quite simply, are:

1. Heisenberg’s uncertainty relation for position and momentum: ΔxΔp ≥ ħ/2.
2. The electric potential energy of the electron in the vicinity of a proton: E = ke²/x, where k is the Coulomb constant, e is the charge of the electron, and x is the distance between the electron and the proton. (Let’s not worry about positive/negative signs here.)
3. And the relationship between a particle’s momentum and its kinetic energy (which we can assume, for these purposes, that the particle is non-relativistic): E = p²/2m, where p is momentum and m is the particle’s mass.

If we note that, approximately, electric potential energy and kinetic energy will balance out, we can set equations 2 and 3 equal to each other, and get that ke²/x = p²/2m. But in this case, x and p can be small, and will be dominated by quantum uncertainty. Therefore, we can approximate that Δx ≈ x and Δp ≈ p, and therefore everywhere we have a “p” in that equation, we can replace it with ≈ ħ/2x. (Or, more accurately, ≥ ħ/2x.)

So our equation then becomes ke²/x ≥ ħ²/8mx², or if we solve this equation for x (multiplying both sides by x²/ke²), we get:

x ≥ ħ²/8mke²,

which is approximately 10^-11 meters, or about a tenth of an angstrom.

Although two atoms can easily have their electron wavefunctions overlap and bind together, this is only generally true of free atoms. When each atom is bound together as part of a much larger structure, the intermolecular forces can frequently keep atoms substantial distances apart, preventing strong bonds from forming except under very special circumstances. The size of an atom will never reduce to zero, but will remain finite, owing to the Heisenberg Uncertainty Principle.

The Heisenberg uncertainty principle, all on its own, is sufficient to explain why atoms don’t collapse and have their electrons spiral into their nuclei. The smaller the distance between the electron and the nucleus becomes — i.e., the smaller that “Δx” in the Heisenberg uncertainty equation gets — the less-well-known momentum “Δp” is, and so as you “squeeze” the distance down to a smaller value, Heisenberg forces your momentum to rise. But higher values of momentum cause the electron to move faster, preventing it from “falling in” to the nucleus, after all. This is the key principle of quantum mechanics that keeps atoms stable, and that prevents the “classical catastrophe” of inspiral and merger from happening.

This also contains with it a profound implication: there is a lowest-energy state that a quantum mechanical system possesses, and that state is not necessarily positive, but can be positive and non-zero, as in the case of one or more electrons bound to an atomic nucleus. We call this a “zero-point energy,” and the fact that there is a lowest energy state has profound implications for the Universe at large. It tells us that you can’t steal energy from the quantum vacuum; it’s already in the lowest-energy state. It tells us that there are no “decays” possible from the lowest-energy stable state; the lowest-energy quantum mechanical systems are stable. And it tells us that any system of quantum particles will have a lowest-energy state to it, determined by the fundamental quantum principles that govern reality. That includes the humble atom, and the Heisenberg uncertainty principle explains why, at a fundamental level, they truly are stable.

The author thanks Will Kinney, in whose excellent book “An Infinity of Worlds: Cosmic Inflation and the Beginning of the Universe” this explanation for the stability of the atom appears. (Now available in paperback.)