Ask Ethan: What Is A Scalar Field?

Travel the universe with Dr. Ethan Siegel as he answers the biggest questions of all

Scalars, vectors, and tensors come up all the time in science. But what are they?

One of the major goals of science is to describe our reality as accurately as possible. If you give us a setup — and tell us what the conditions of a system are — and our best scientific theories are powerful enough, science will be able to predict for you precisely how that system will evolve into the future. If we can measure and know the properties of whatever it is we’re dealing with, from atoms to humans to planets to stars and galaxies and more, a useful scientific theory will be able to predict what they will be like a finite time from now. But sometimes, understanding what a scientific theory is, does, or even means requires that we learn some terms we’re unfamiliar with, including ones that have their roots in mathematics and often aren’t intuitive. That’s what’s tripping up Elen Sentier, who asks:

“Help! I’m getting somewhere with your piece on string theory but I haven’t a clue what a scalar field is. I have no maths and no physics but I love the ideas and concepts. Can you explain a scalar field in words of 2 syllables please?”

This is a perfectly reasonable request, but one that’s a challenge even for a seasoned scientist or science communicator. From hereon out, let’s teach you what a scalar field is, and why it matters, in the simplest terms we can find.

Planet Earth, as viewed by NASA’s Messenger spacecraft as it departed from our location, clearly shows the spheroidal nature of our planet. This is an observation that cannot be made from a single vantage point on our surface. (NASA / MESSENGER MISSION)

Let’s say you want to describe our planet: Earth. There are a number of things we can choose to look at and study. For instance, we can decide to look solely at Earth’s surface, and ask questions about the terrain at every point on the globe. In an instant, you can start thinking of certain things you might like to know. They include:

Where are we looking, right now, in terms of place?
When is the instant in time that we’re concerned about?
What is our height above the “sea level” of Earth’s surface?
If I put down a ball, which way will it roll, and how fast will it roll down that slope?
Is there any stress or strain on the Earth at that point?
If I put down a large amount of water, how will the water flow? What route will it take and how fast will it go? Will it develop eddies or a vortex anywhere?

The Earth itself is just one object to think about, but thinking about the surface of our planet gives us a great way to think about what a field is, as well as the different types of fields that matter for science.

The diameter of the Earth at the equator is 12,756 km, while at the poles it’s only 12,714 km. You are 21 kilometers closer to the center of the Earth standing at the North Pole than you are at the equator. This difference is largely due to Earth’s axial rotation. There are also other features like mountains, valleys, hills, and more superimposed atop this overall oblate spheroid shape. (NASA / BLUE MARBLE PROJECT / MODIS)

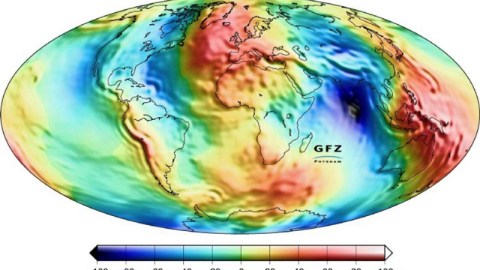
Let’s start with the question of height. If the Earth were perfect, smooth, and didn’t rotate, it would form an exact sphere. Because the Earth rotates, that shape gets compressed at the poles and bulges in the middle, forming a shape known as an oblate spheroid. Still, there are ups and downs all along the surface, with the oceans, seas, lakes, and rivers filling some of the deep depths with water.

Everywhere on the surface, then, we can ask a question like, “What is our height above Earth’s sea level?” where sea level is the height at which every point on Earth would be covered in ocean if there were no land masses that rose above it. So if you want to describe “what your height is above sea level” at every point on the surface of Earth, how would you do it?

That’s exactly the case that would call for a scalar field.

The northern 40% of Mars is roughly 5 kilometers lower in elevation than the rest of the planet, as this topographic map shows. That giant feature, known as Borealis Basin, was likely created by a large impact that could have kicked up enough debris to form many moons. (NASA / JPL / USGS)

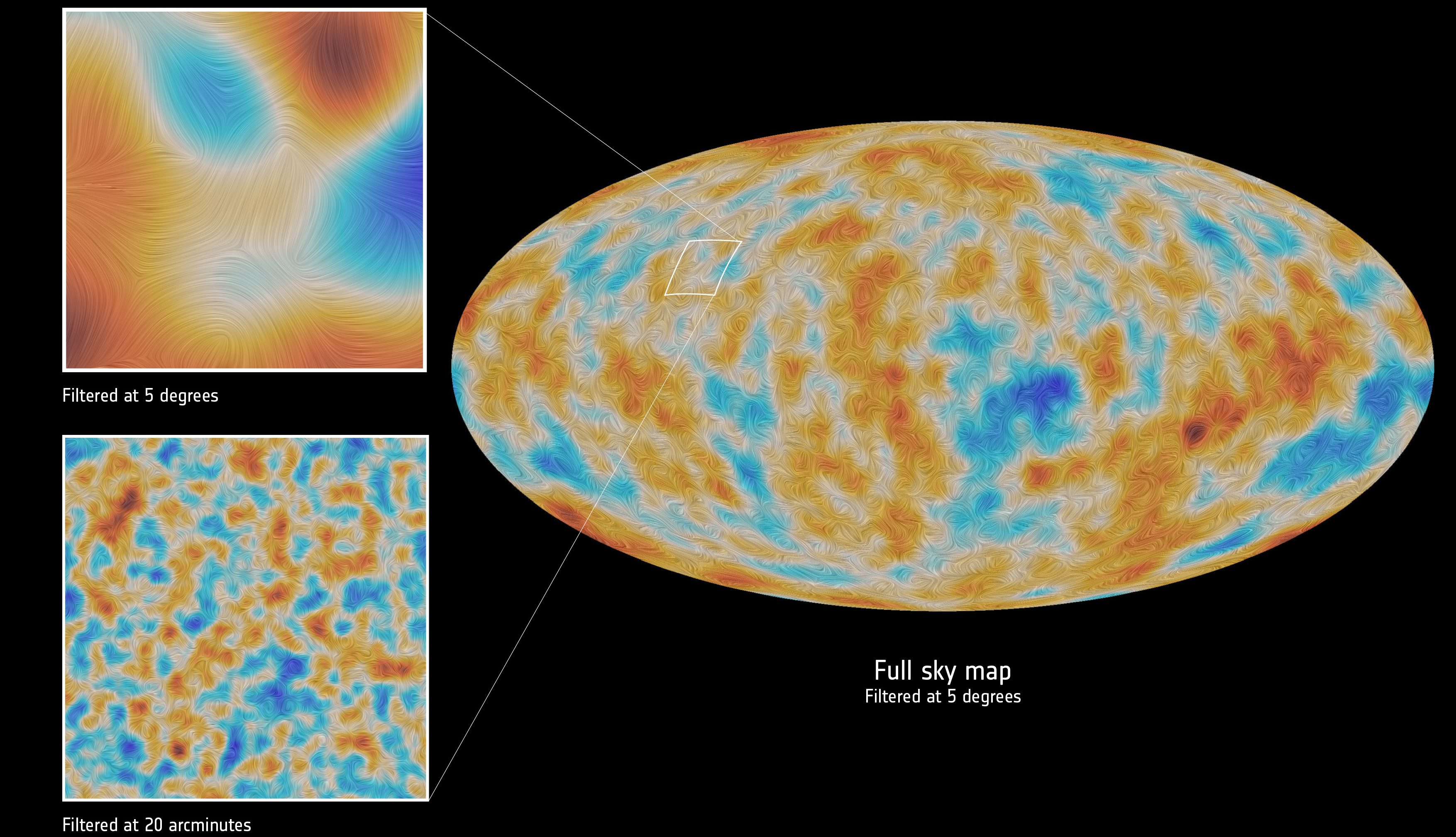
A scalar field is, to be frank, the most simple type of field you can have. What it says is, if you give the values that tell you “where” and “when” you are — where you are in space and when you are in time — the scalar field will give you one and only one value that describes the “amount” of stuff you’re trying to measure. If that thing you’re asking about is “height above sea level,” then the scalar field can tell you that height. Not just on average, or over the whole surface, but at each and every point. If the height of the Earth were something that changed over time (and over long enough timescales, it does), a scalar field could capture that, too.

But that scalar field won’t tell you all you’d ever want to know about the Earth’s surface. It just tells you “what the value of the thing I’m asking about at any point in space and/or at any moment in time is.” If you wanted, instead, to know the answer to some of the other questions like, “Which way will water flow down this surface?” a scalar field just isn’t enough.

For that, you’d need a slope map instead, and that’s not a scalar field, but a vector field.

The terrain shown here, which illustrates Mount Sharp on Mars from the Curiosity rover, has many properties to it: elevation and slope, for example, at every point. Simply giving the elevation at every point would be a scalar quantity; giving the slope at every point is a vector quantity. (NASA/JPL-CALTECH/MSSS)

So what is a vector field, then, and how is it different from a scalar field?

A vector field doesn’t just tell you what the “value” of something is at each and every point in space and time, but tells you a value and also which way that value points in some sense. A river will always flow, at any point, at a certain speed, but speed alone is not enough to describe its motion in full. The river also flows a certain way along a certain heading: we need to know which way it goes, not just how fast it’s going.

There’s an extra thing that we can do with a vector field that we cannot do with a scalar field: we can have a vector field give rise to a “curl,” which describes how objects move around a certain point in space. In math, the curl of a scalar field is always zero, so if all we used were scalar fields, we could never have a vortex, a whirlpool, a twister, or motion that describes going around in a circle. If you point your thumb one way and look at how your fingers want to wrap around your hand, that wrapping motion you’ll try to make is one way to conceive of a curl.

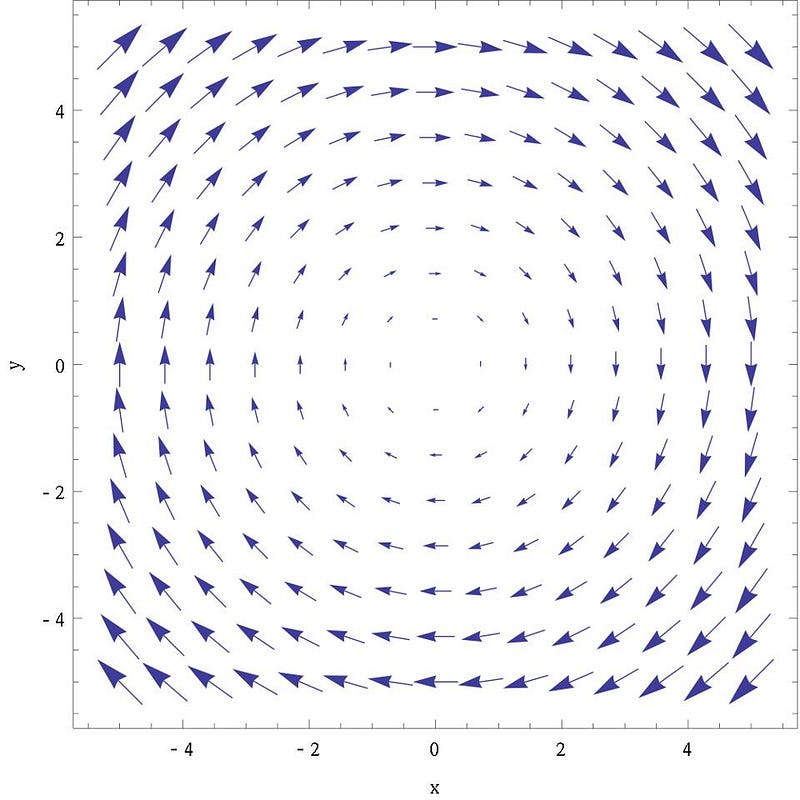
This illustration shows a uniform, two-dimensional vector field representing a curl. The clockwise nature of the curl can be obtained in two ways: either by pointing a fundamentally left-handed quantity like your left thumb toward you, where your fingers curl in the clockwise direction, or by pointing a right-handed quantity, like your right thumb, away from you. (LOODOG AT ENGLISH WIKIPEDIA)

In our concrete, real world, scalar fields can get us very far, but they can’t get us any old thing we can dream up. To account for motion, we need to know which way things are going, and that means a vector field. To explain forces, and hence, how motion changes over time, we need not just the amount of force, but also which way that force points. For spinning motions, as things rotate or revolve around other objects, we also need vector fields; do things curl the way your fingers curl around your right hand or your left?

Think about all the different traits that an object might have that you might want to know, measure, or use to predict the outcome of a system that’s set up a certain way. Almost all of them can be described fully by either a scalar (just knowing the amount is enough) or a vector (where the amount and also which way it points is important) field.

Mass is a scalar.
Speed is a scalar.
Height is a scalar.
Distance is a scalar.
Time elapsed is a scalar.
Slope is a vector.
“Which way” is a vector.
Torque is a vector.
Force is a vector.

Well, mostly on that last one.

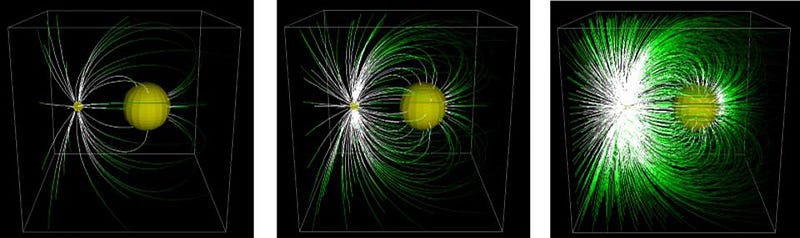
Electric fields and electric forces are all well-described by vectors, as they possess both a magnitude and a direction, with no other properties associated with them. If things only have a magnitude, like voltage, they can be described with a scalar field. More complex entities, like gravitation, can require extra parameters, necessitating a tensor field instead. (PAUL FALSTAD’S 3-D VECTOR FIELDS APPLET)

In the eyes of Newton, a force is always a vector. It has a strength and it goes along a certain heading, and that’s enough to describe it fully. Between two charged objects, that force is a vector. Inside an atom’s core, those forces — between protons and neutrons and even inside a proton itself — are all vectors.

But in the eyes of Einstein, when it comes to the most famous force of all (the one that occurs between all massive objects, but that has too many word-parts to use here), force is neither a scalar nor a vector, but requires something even more complex to describe: a tensor.

So what’s a tensor, then?

Picture a solid object like a cement pillar. You have it, you watch it, and you subject it to a lot of real-world factors. It gets hot and cold. It has weight placed atop it and removed. People push it, pull it, or lean against it. The masses around it all pull (or push) on it. If you could map out all the different forces acting inside the pillar, including things like strains and stresses, you’d find that they not only varied with time and in which ways they pointed, but that even a vector field wasn’t enough to describe it. Instead, you’d need something even more broad, that can include things scalars and vectors couldn’t. That’s when you need a tensor.

Sweden has a museum dedicated to disgusting foods, and this 2018 exhibit shows a “Jell-O Salad” from the United States. If you poke a Jell-O mold, you’ll watch the gelatinous material wiggle and deform as a result. The forces and deformations internal to the Jell-O mold itself cannot be described by either a scalar or a vector field, but require something more complex: a tensor field. (JONATHAN NACKSTRAND/AFP via Getty Images)

If you were to push on something along a precise heading, you’d expect the force to go that same way: along that distinct axis that you pushed it. But sometimes — and you can poke a congealed Jell-O mold if you want to see the effect in action for yourself — a starting force that points one way can create forces within an object (or on an object) that point along different axes than the initial action that started it all. This creates forces along lines you could not explain if you only worked with scalar or vector fields.

This was the key to Einstein’s great idea. If you can, from any point of view that you choose, tell us:

where all the masses, photons, and other quanta are,
what their mass and mass-like values are,
how they are placed,
and how they are moving at any one point in time,

then Einstein’s theory can tell you, at every point in space and time, how space will curve, and how space will tell matter and photons and every other quantum how to move.

An animated look at how spacetime responds as a mass moves through it helps showcase exactly how, qualitatively, it isn’t merely a sheet of fabric. Instead all of 3D space itself gets curved by the presence and properties of the matter and energy within the Universe. Multiple masses in orbit around one another will cause the emission of gravitational waves. (LUCASVB)

This theory — the biggest science exploit of Einstein’s life — is purely a tensor theory. There is no scalar part; there is no vector part. In fact, there are very strong limits on how much a “scalar” or “vector” part can contribute to how spacetime curves. If we want to get the cosmos that we know and observe, we cannot have scalar or vector parts to the law that governs spacetime.

And that is one big problem with string theory. String theory doesn’t give you 3D space (or 4D spacetime), but rather six extra ones that you have to get rid of. It doesn’t give you a tensor theory that tells you how mass curves spacetime, but rather a theory with both scalars and tensors, and you have to purge the theory of all the scalar ones. Put simply, it gives you “extra stuff” to your cosmos that our cosmos does not have.

One of the toughest tests comes from LIGO, which has seen ripples in spacetime from more than 50 events as of today. The way they deform the fabric of space shows a purely tensor nature, with very little wiggle room for scalar or vector parts to even exist; the constraints have gotten very tight.

When a gravitational wave passes through a location in space, it causes an expansion and a compression at alternate times in alternate directions, causing laser arm-lengths to change in mutually perpendicular orientations. Exploiting this physical change is how we developed successful gravitational wave detectors such as LIGO and Virgo. (ESA–C.CARREAU)

All in all, a scalar field can only give you an “amount” of something, but it can give it to you at every point in space at any time that you choose. If you want to add in something more, like which way an amount of something points, you need to upgrade to a vector field. And if you have something even more complex, like:

space that is curved,
stresses and strains,
or effects that point along different headings from the force that begat it,

even a vector field can’t capture all of them. For that, you need a tensor field, like Einstein’s theory of how mass, matter, and more curve spacetime.

(One book I like that goes into the gory details about the difference between scalars, vectors, and how they allow us to derive different features of our real world is called Div, Grad, Curl, and All That; if you struggled with advanced math in college, this can help make some complex ideas more clear.)

A scalar field is just a field that has a value — or amount — assigned to it and nothing else. If you want to know anything else, even as simple as which way something points, a scalar simply won’t do. There may be extra scalars floating around out there in the form of fields or quanta we have yet to meet, but as far as we know, there isn’t one that’s part of Einstein’s theory. Finding out why is one challenge string theory has yet to surmount.

Send in your Ask Ethan questions to startswithabang at gmail dot com! (And yes, I know that startswithabang is more than 2 syllables!)

Starts With A Bang is written by Ethan Siegel, Ph.D., author of Beyond The Galaxy, and Treknology: The Science of Star Trek from Tricorders to Warp Drive.

Travel the universe with Dr. Ethan Siegel as he answers the biggest questions of all