Ask Ethan #31: Why are we made of matter?
If the Universe began with equal amount of matter and antimatter, why does matter dominate today’s cosmos?
“You may not feel outstandingly robust, but if you are an average-sized adult you will contain within your modest frame no less than 7 × 10^18 joules of potential energy—enough to explode with the force of thirty very large hydrogen bombs, assuming you knew how to liberate it and really wished to make a point.” –Bill Bryson
At the end of every week, I go through the best of your submitted questions and suggestions, and choose one to be the subject of our weekly Ask Ethan column. This week’s honor goes to Justin Starr, who asks the following:
My understanding is that in the nascent universe, there were equal parts matter to antimatter, followed by serious matter/antimatter annihilation. Why (How) did matter win out in the end?
Justin is asking about one of the great unsolved mysteries of our Universe.
Think about these two seemingly contradictory facts:
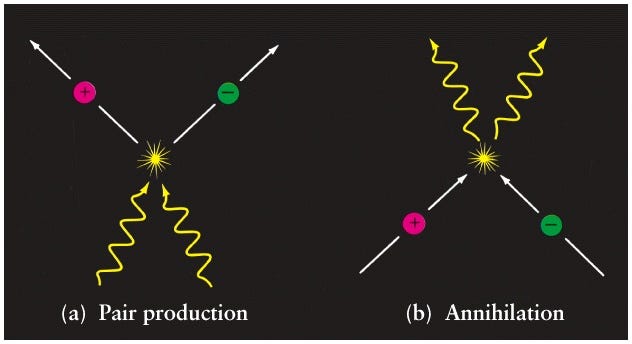
1.) Every interaction between particles that we’ve ever observed, at all energies, has never created or destroyed a single particle of matter without also creating or destroying an equal number of antimatter particles. The physical symmetry between matter and antimatter is even more stringent than this:
- every time we create a quark, we also create an antiquark,
- every time a quark is destroyed, an antiquark is also destroyed,
- every time we create-or-destroy a lepton, we also create-or-destroy an antilepton from the same lepton family, and
- every time a quark-or-lepton experiences an interaction, collision or decay, the total net number of quarks and leptons at the end of the reaction (quarks minus antiquarks, leptons minus antileptons) is the same at the end as it was at the beginning.
The only way we’ve ever made more (or less) matter in the Universe has been to also make more (or less) antimatter in equal amounts. And yet, there’s this second fact:

2.) When we look out at the Universe, at all the stars, galaxies, gas clouds, clusters, superclusters and largest-scale structures everywhere, everything appears to be made of matter and not antimatter. Whenever and wherever antimatter and matter meet in the Universe, there’s a fantastic outburst of energy due to particle-antiparticle annihilation.
We actually observe this annihilation in some locations, but only around hyper-energetic sources that produce matter and antimatter in equal amounts. When the antimatter runs into matter in the Universe, it produces gamma rays of very specific frequencies, which we can then detect.
But if we look at the interstellar and intergalactic media — the space between stars within galaxies and the space between galaxies on even larger scales — we find that it’s full of material, even if there aren’t any stars in many of those regions. Space is vast, of course, and the density of matter is sparse, so you might be wondering if you threw a single antimatter particle (say, an anti-proton) into the mix, how long it would last before running into a particle of matter an annihilating, on average.

In our own galaxy’s interstellar medium, the mean lifetime would be on the order of about 300 years, which is tiny compared to the age of our galaxy! This constraint tells us that, at least within the Milky Way, the amount of antimatter that’s allowed to be mixed in with the matter we observe is at most 1 part in 10^15!
On larger scales — of galaxies and galaxy clusters, for example — the constraints are less stringent but still very strong. With observations spanning from just a few million light-years away to over three billion light-years distant, we’ve observed a dearth of the X-rays and gamma rays we’d expect from matter-antimatter annihilation. What we’ve seen is that even on large, cosmological scales, 99.999%+ of what exists in our Universe is definitely matter (like us) and not antimatter.
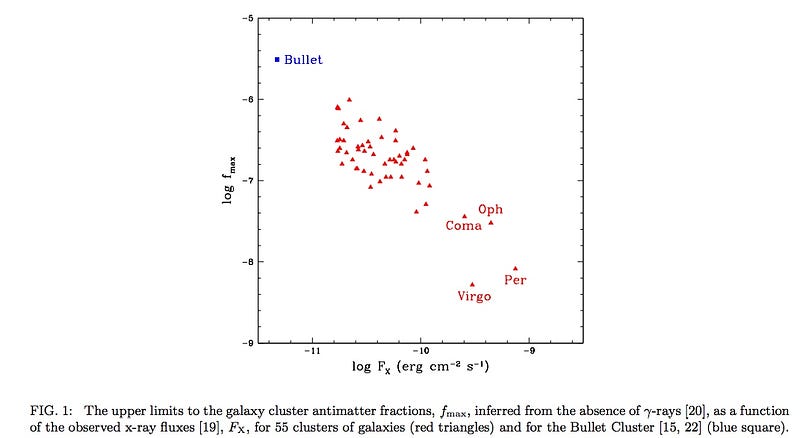
And that’s a lower limit as to how severely matter dominates antimatter in the Universe, observationally.
So on the one hand, we’ve got our experimental results that show an inability to create or destroy matter without also creating or destroying an equal amount of antimatter, and on the other hand, we’ve got our Universe, which appears to be — to the best of our knowledge — made up of practically 100% matter, and practically 0% antimatter. So what gives?
If we want to understand how this could have happened, we have to go all the way back to the very early Universe, just after inflation ended and the Big Bang occurred: to a time when the Universe was hot, dense, and full of matter, antimatter and radiation.

In the earliest stages of the Universe, everything we know of was incredibly hot and dense. The part that makes up our observable Universe today contained some 10^90 (or so) particles of matter, antimatter and radiation, with matter and antimatter presumably in equal amounts. Things were so energetic that whenever any two particles collided, they could produce matter and antimatter in equal amounts spontaneously, and when matter and antimatter collided, they’d revert into pure radiation. And this was happening everywhere, all the time.
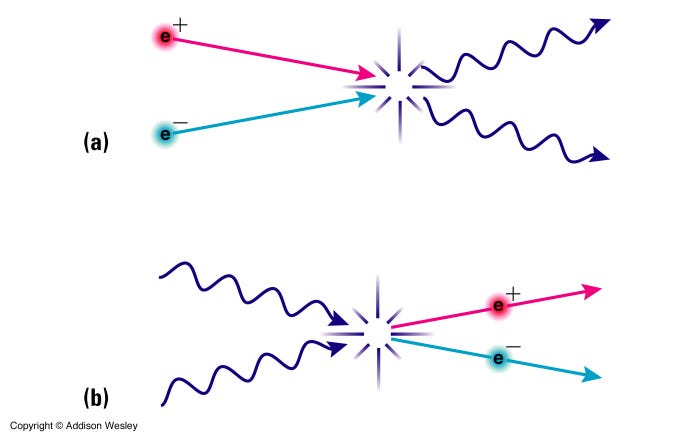
If all the Universe were able to do was create matter/antimatter pairs and have them annihilate again, our Universe would have looked very different than it does today. Theoretically, if there were no matter/antimatter asymmetry, as the Universe cooled and expanded, we would have quickly reached a point where creating new pairs would be impossible, the existing matter-and-antimatter pairs would annihilate until things were so sparse that they couldn’t find one another anymore, and we’d be left with a Universe that was filled with mostly photons and a small amount of both matter and antimatter left over.
How much would’ve been left, quantitatively? To the best of our knowledge, about 10^70 particles of matter and antimatter each, for a photon-to-proton ratio of about 10^20. In other words, there would have been approximately 100,000,000,000,000,000,000 photons for every one proton in the Universe, and an equal number of antiprotons to protons.
But we can actually measure what the photon-to-proton ratio is.
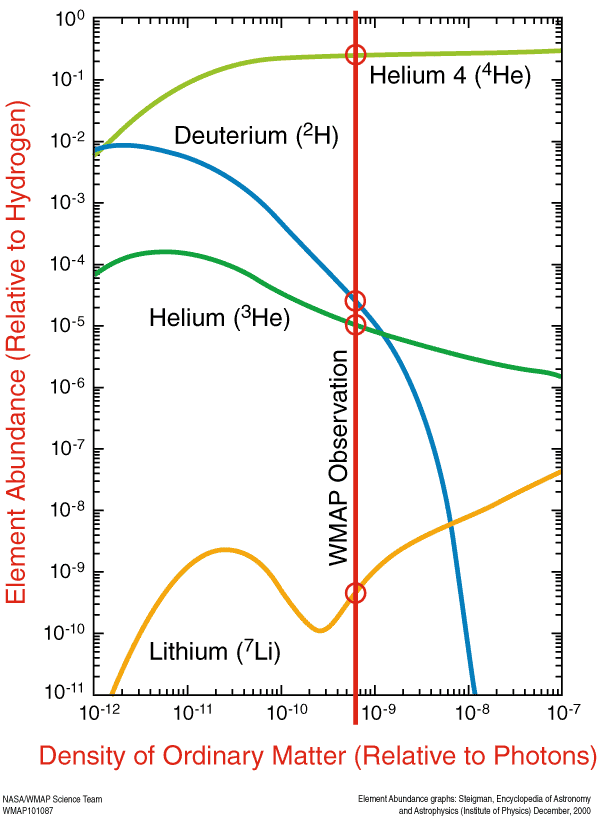
And it’s not nearly so severe an asymmetry. Yes, there are many, many times more photons than protons, but the ratio is more like a couple-of-billion-to-one (with pretty much no antimatter), telling us that something happened in the very early Universe to create a fundamental matter-antimatter asymmetry. And to the best of our observations, that asymmetry happened everywhere (and happened with the same magnitude everywhere) that we can see.

Now if you want to know how this happened, welcome to the club. This is the problem of baryogenesis, and it’s one of the greatest unsolved problems in fundamental physics. But just because we don’t know exactly how this could’ve happened doesn’t mean we don’t have a good general idea of how this happened! In particular, Andrei Sakharov showed that if you meet just three conditions, you can create a matter-antimatter asymmetry from an initially symmetric state:
- Out-of-equilibrium conditions,
- C-violation and CP-violation, and
- Baryon-number-violating interactions.
That’s it. Those three things. And to the best of our knowledge, the Universe should have all three of these!
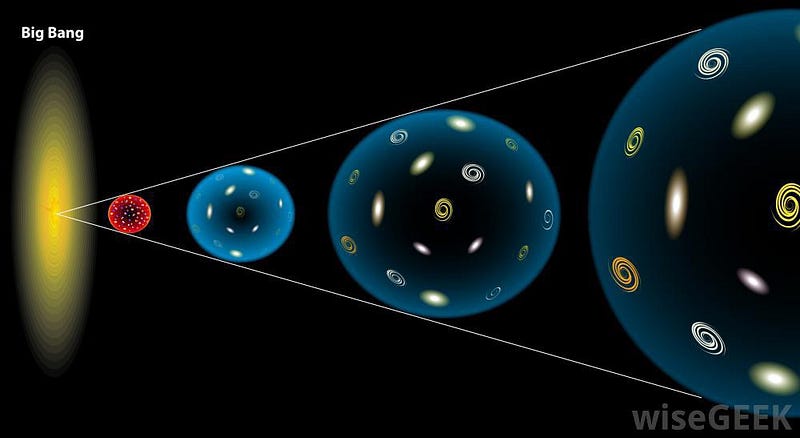
Out-of-equilibrium conditions. This is the easy one. If you have a large, hot, expanding-and-cooling Universe governed by general relativity and the laws of quantum field theory, congratulations: you have out-of-equilibrium conditions! Equilibrium, remember, is when all the particles in a system have a chance to communicate — or exchange information — with one another. But in our expanding, cooling Universe, particles on one side are causally disconnected from particles on the other one; in fact, in the very early Universe, there are some 10^50+ causally disconnected regions, where even light would not have enough time to reach from one region into the others.
The early Universe was not only out-of-equilibrium, but you’d be hard-pressed to design a system, even in principle, that was more out-of-equilibrium than this one.
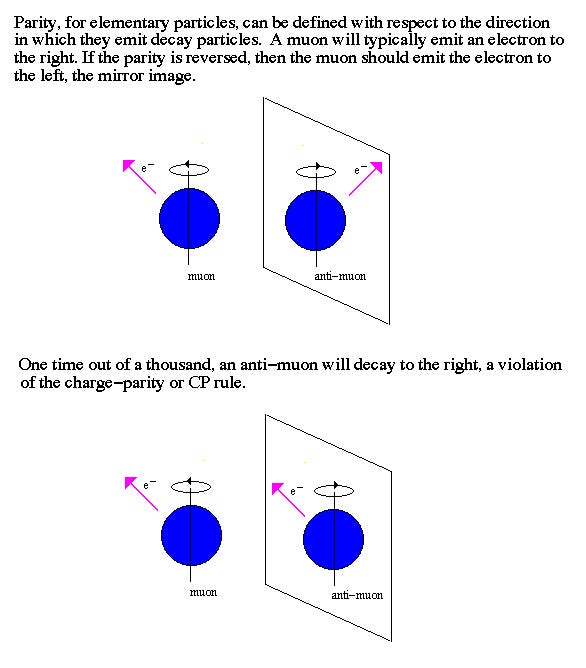
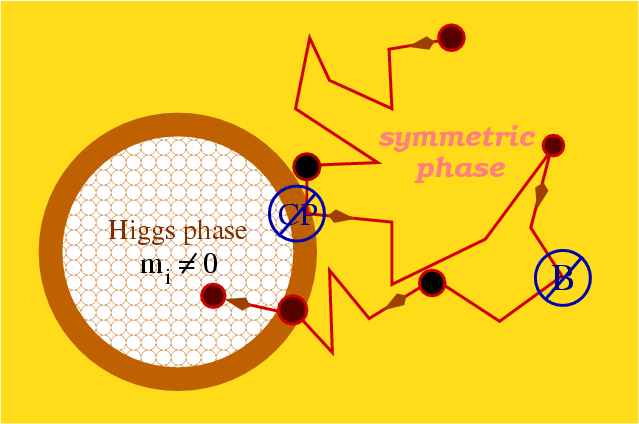
C-violation and CP-violation. C stands for charge conjugation (meaning replace all the particles with antiparticles, and all the antiparticles with particles), and P stands for parity (which means reflect everything in a mirror). Basically, C and P are conserved if you impose the symmetry and the laws of physics — and all physical phenomena — remain unchanged, and CP is conserved if you can impose both symmetries simultaneously and all phenomena remain unchanged.
In our Universe, the gravitational, electromagnetic and strong interactions all appear to conserve C, P, and CP. But the weak interactions violate them! In particular, the decays of mesons containing strange quarks (kaons) and bottom quarks (B-mesons) are known to violate C, P, and CP quite severely, meaning that there are some fundamental behavioral differences between particles and their antiparticle counterparts. So we’ve got two of the three.
And finally…

Baryon-number violating interactions. This is a very tricky one, because we’ve never experimentally observed the creation of a quark without an antiquark counterpart. (And a baryon is simply any particle made up of three quarks, like a proton or neutron. Remember, quarks only exist in nature in bound states!) But if we look at the Standard Model of particle physics, we know it can — nay, must — have these kinds of interactions.
What I’m about to show you is the field equations that govern the Standard Model of particle physics. (Don’t worry about the details, please.)
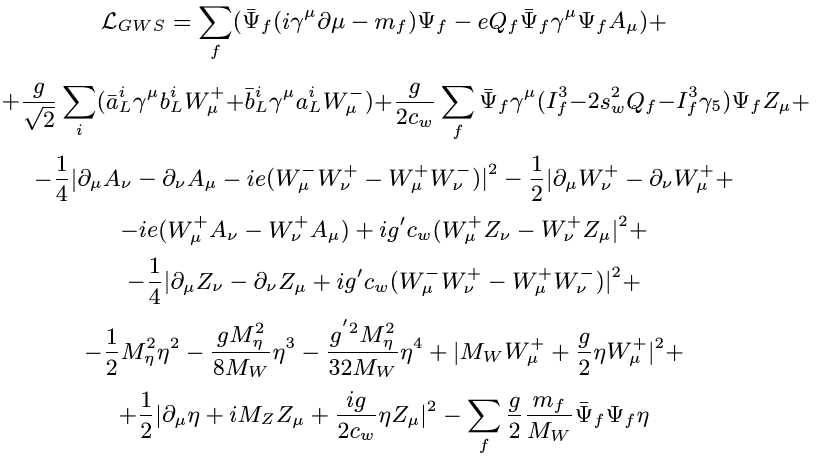
What’s important about this is that there is a mathematical property of this equation known as an anomaly that is required for a number of particle decays we see — such as the decay of the neutral pion — that also allows for the violation of baryon number. In fact, what it explicitly allows for is violation of both baryon (e.g., a proton) and lepton (e.g., an electron) number, but that they must be violated together, meaning the Universe must have the same total number of baryons and leptons! (This neatly explains why there are an equal number of protons and electrons, and hence why the Universe not only has protons and electrons, but is still electrically neutral.)
The big question, of course, comes when we start putting the numbers in. Based on:
- The amount the Universe is out-of-equilibrium,
- The amount of C– and CP-violation observed, and
- The amount that the Standard Model violates baryon number,
do we get enough baryon-number violation?
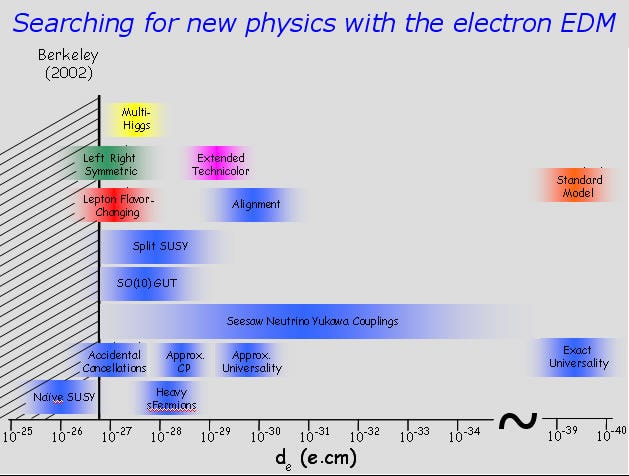
The answer — to the best of our present knowledge — looks like no, not quite. (We’re still a factor of a few tens of millions too low.) Now, there could be a lot more CP– violating interactions in the Standard Model at higher energies that we simply haven’t discovered yet, but the most common assumption is that there is physics beyond the Standard Model that allows for a greater amount of either CP-violation or baryon number violation.
Some possibilities include (but are not limited to):
- The Affleck-Dine mechanism, which relies on supersymmetry,
- Standard model extensions at the electroweak scale,
- Leptogenesis, where a fundamental lepton asymmetry is created (perhaps from new neutrino physics) and then the baryon asymmetry arises from that, or
- GUT-scale baryogenesis, where new physics at the scale of electroweak unification with the strong force allows us to create more matter than antimatter.
These are probably just meaningless words to you, so allow me to walk you through an example of how this could happen using the GUT-scale scenario. (Disclaimer: this is not how it probably actually happens; this scenario is for illustrative purposes only.)
Imagine the early Universe, full of radiation, and all kinds of particles and antiparticles, the latter of which exist in equal numbers to one another. Some of them are quarks and antiquarks, some are leptons and antileptons, some are bosons (and their antiparticles, where applicable; many bosons are their own antiparticles), etc.
Now imagine that there’s a new type of particle that couples to both quarks and leptons, and imagine that it’s charged. I’ll name it the Q-particle.

Initially — just like for all matter-and-antimatter particles — it gets created in the hot, early Universe in pairs. Sometimes the Q+, the matter version, finds a Q-, the antimatter version, and they annihilate, and sometimes other particles collide with enough energy to create a Q+/Q- pair.
This goes on for a little while in the early Universe (some tiny fraction of a second), and then the Universe cools. Suddenly, you can’t produce new Q+/Q- pairs any more, and while some of the existing Q+/Q- pairs will annihilate and become radiation again, the rest of them — being unstable, short-lived particles — will decay.
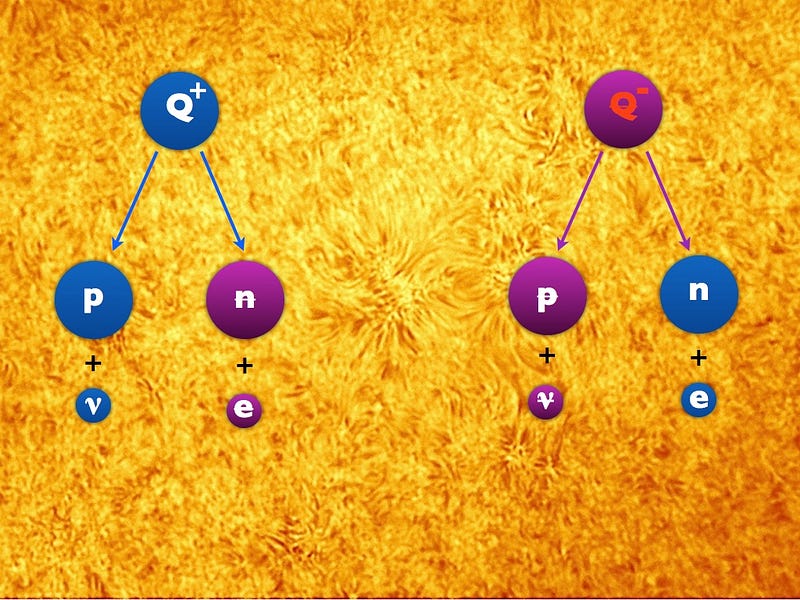
Because of the laws of particle physics (even if we allow extensions to the Standard Model), there are still some symmetries that must hold. The Q+ and Q- particles must have the same:
- total mean lifetimes,
- decay pathways, and
- still conserve charge, mass, and “baryon minus lepton” number.
So in this example, the Q+ and Q- each have the same mean lifetime, a “baryon minus lepton” number of zero, and while the Q+ can decay into a proton and neutrino pair or an anti-neutron and anti-electron pair, the Q- can decay into an antiproton and antineutrino pair or a neutron and electron pair. These violate both baryon number and lepton number, but not the “baryon minus lepton” combination. This scenario is both possible and reasonable, but would create no inherent baryon asymmetry unless we introduced CP-violation.
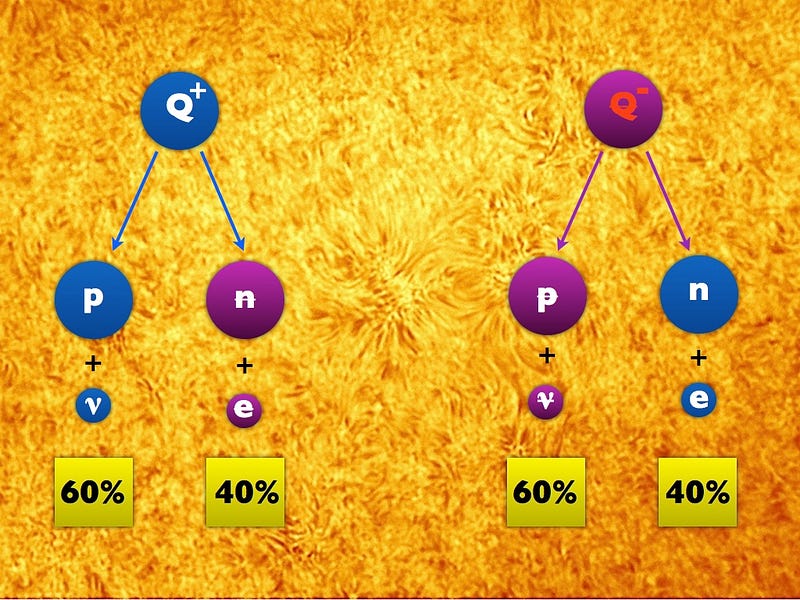
With no CP-violation, what we call the branching ratios — or the fractions of Q+ particles and Q- particles that decay through each channel — would be identical. If 60% of Q+ particles decayed into protons and neutrinos, then 60% of Q- particles would decay into antiprotons and antineutrinos. The other decay channel could be 40% for both the Q+ and the Q-, again conserving the CP symmetry.
But if we allow for CP-violation, the branching ratios between particles and antiparticles are allowed to be different! So long as the total decay rate for the Q+ and Q- particles are still identical, the laws of physics still abide this behavior. So let’s introduce some CP-violation now.
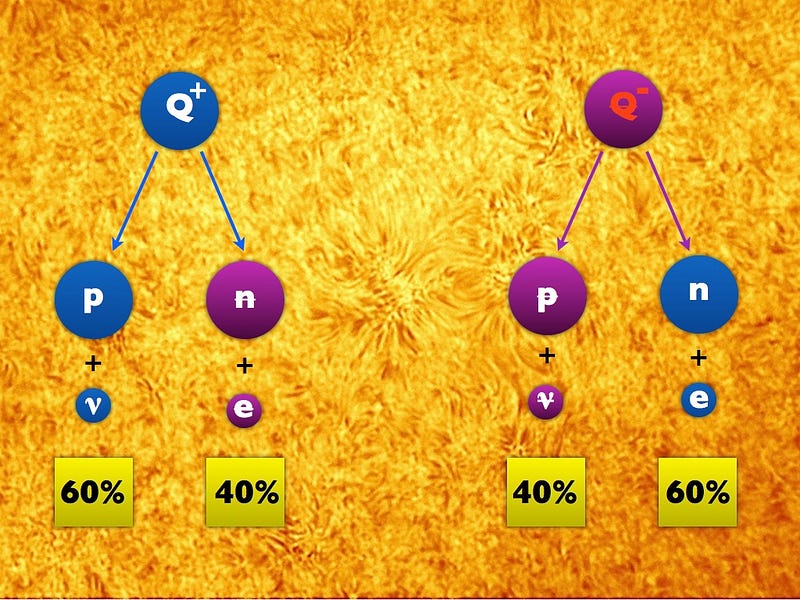
Notice the very subtle difference: the Q+ still decays in the same exact way as before, but now the Q- has more decays into neutrons and electrons, but fewer decays into antiprotons and antineutrinos!
When all the Q+ and Q- particles have decayed — ignoring the leptons (for clarity’s sake) — what do we have left?
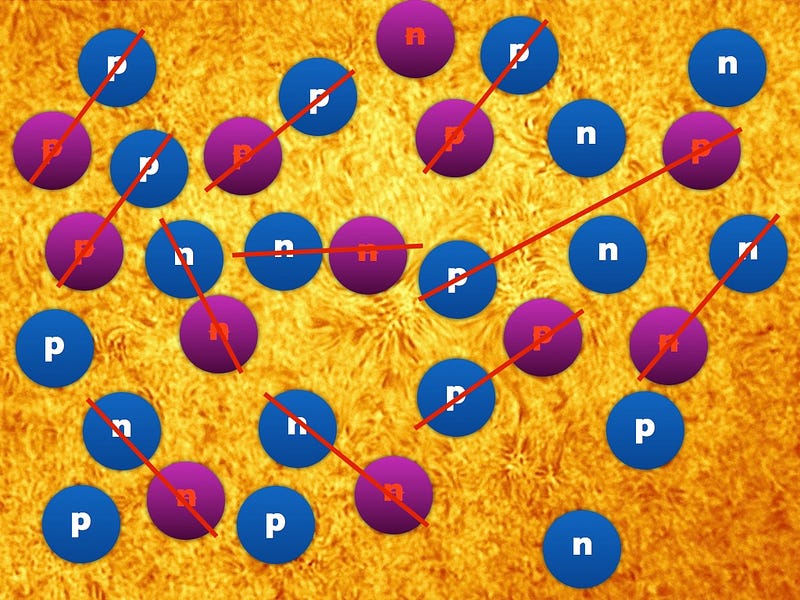
There are a bunch of protons, neutrons, antiprotons and antineutrons that result from these decays. Over time, the antiprotons and protons will find one another and annihilate, and so will the neutrons and antineutrons. But because of the decay asymmetry between the Q+ and Q- particles, there were more protons created than antiprotons, and more neutrons than antineutrons.
After all the particle-antiparticle pairs annihilated away, there was still a leftover baryon asymmetry. If we keep track of the lepton asymmetry, we’d find that there were a number of electrons exactly equal to the number of protons, and more neutrinos than antineutrinos by exactly the number of neutrons.
And although this is probably not the exact mechanism by which baryogenesis happened, something akin to this very likely did, and gave rise to the Universe we see today!

Those three Sakharov conditions,
- The Universe being out-of-equilibrium,
- The existence of C- and CP-violation, and
- The violation of baryon number conservation,
surely exist in our Universe, and the only question we have left to answer is exactly, “how did we get the amount of the matter-antimatter asymmetry we have today?” This is the answer to the best of our knowledge today, and I’m not ashamed to say that it’s incomplete. But of all the great mysteries relating to “where all of this came from,” this is one I’d bet on our ability to successfully answer within my lifetime.
Thanks for a great question, Justin, and I hope you enjoyed this week’s Ask Ethan. If you have a question or suggestion you’d like considered, submit yours here, and the next column could feature you!
Have a comment? Weigh in at the Starts With A Bang forum on Scienceblogs!





