How the quadratic formula evolved, from Babylon to modern math class
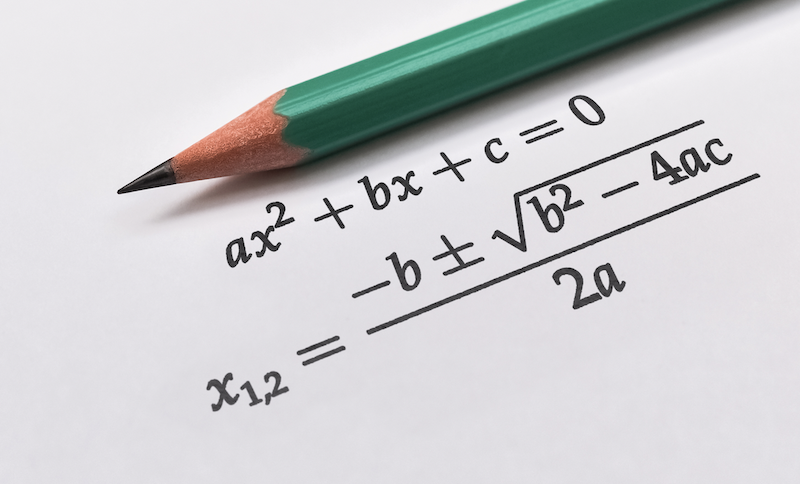
- In his new book, The Art of More: How Mathematics Created Civilization, author Michael Brooks explores the evolution of mathematics and its wide-ranging impacts on ancient and modern societies.
- This excerpt overviews the evolution of algebra and, more specifically, the quadratic formula.
- What started as a tax-collecting tool evolved into a formula that schoolchildren still learn today.
Excerpted from THE ART OF MORE: HOW MATHEMATICS CREATED CIVILIZATION by Michael Brooks. Copyright © 2022 by Michael Brooks. Excerpted by permission of Pantheon Books, a division of Penguin Random House LLC. All rights reserved. No part of this excerpt may be reproduced or reprinted without permission in writing from the publisher.
Solving the quadratic equation
What even is algebra? You might think of it — quite justifiably, given how it has traditionally been taught — as a terrifying labyrinth of equations, an alphabet soup of x, y, z, a, b, and c, plus some superscripts (2 and 3 and maybe even 4). To the uninitiated, it is certainly off-putting. But there’s no reason algebra should be problematic. It’s really just the art of teasing out hidden information using what we do know.
Algebra’s name comes from the word al-jabr in the title of Muhammad al-Khwārizmī’s 9th-century book (we met it in Chapter 1 as The Compendious Book on Calculation by Completion and Balancing). This pulls together Egyptian, Babylonian, Greek, Chinese, and Indian ideas about finding unknown numbers, given certain others. Al-Khwārizmī gives us prescriptions — formulas we call algorithms — for solving the basic algebraic equations such as ax2 + bx = c, and geometrical methods for solving 14 different types of ‘cubic’ equations (where x is raised to the power of 3).
At this point in history, by the way, there was no x, nor anything actually raised to any power, nor indeed any equations in what al Khwārizmī wrote. Algebra was originally ‘rhetorical’, using a convoluted tangle of words to lay out a problem, and to explain the solution. The sought-after hidden factor was usually referred to as the cossa, or ‘thing’, and so algebra was often known as the ‘Cossick Art’: the Art of the Thing. An early student of the Cossick Art might find themselves face to face with something like this:
Two men were leading oxen along a road, and one said to the other: “Give me two oxen, and I’ll have as many as you have.” Then the other said: “Now you give me two oxen, and I’ll have double the number you have.” How many oxen were there, and how many did each have?
or
I have a single linen cloth which is 60 feet long and 40 feet wide. I wish to cut it into smaller portions, each being 6 feet in length, 4 feet in width, so that each piece is big enough to make a tunic. How many tunics can be made from the single linen cloth?
These examples were collected by Alcuin of York in around ad 800, and published in a compendium of puzzles called Problems to Sharpen the Young. They’re not that different from the questions we faced in maths lessons at school. However, we had the advantage of being able to turn them into equations; it is worth pausing, before we go deeper into algebra, to appreciate how privileged this makes us.
It was only in the 16th century that anyone thought to move algebra away from words. The idea came to a French civil servant called François Viète. After training as a lawyer, Viète spent most of his professional life in the service of the French royal court, helping out in any way he was asked to. He was an administrator in Brittany, a royal privy counsellor to Henry III, and codebreaker to Henry IV. Viète’s proudest moment might have come when the king of Spain accused the French court of sorcery. How else, he complained to the Pope, could France have foreknowledge of Spain’s military plans? But there was no sorcery, of course. Viète was simply cleverer than Spanish codemakers, and had been able to decrypt their communications when French soldiers intercepted them.
It was perhaps this same mental agility that enabled Viète to see that rhetorical algebra would be easier if it was encoded as symbols. In his algebra, he used consonants to designate parameters, and vowels for the unknown items. He would write something like:
A cubus + B quad. in A, æquetur B quad. in Z
where we would now write
A3 + B2A = B2Z
It still wasn’t plain sailing , if we’re honest, but it was a start. It is interesting to note that the sign for plus is here (and he used minus signs elsewhere), but the equals sign is not. Welsh mathematician Robert Recorde introduced our equals sign in 1557, in his snappily titled book The whetstone of witte, whiche is the seconde parte of Arithmetike: containyng the xtraction of Rootes: The Cossike practise, with the rule of Equation: and the woorkes of Surde Nombers.
And while we’re on the subject of notation, it’s worth noting that the reason that the letter ‘x’ became associated with the unknown thing is still hotly disputed. According to cultural historian Terry Moore, it’s because al-Khwārizmī’s original algebra used al-shay-un to mean ‘the undetermined thing’. When medieval Spanish translators were looking for a Latin equivalent, they used the closest thing they have to ‘sh’, which doesn’t actually exist in Spanish. And so we ended up with the letter that makes the Spanish ‘ch’ sound: x. But other sources say that it is down to René Descartes, who simply put the two extremes of the alphabet to work in his 1637 book La Géométrie. He generalized the known parameters to a, b, and c; the unknowns were designated x, y, and z.
If you are intimidated by the idea of algebra, with all its enigmatic notation, you might benefit from thinking of it as just a way of translating geometric shapes into written form.
In structuring this book, I have drawn an artificial distinction between algebra and geometry. Although we typically learn them as distinct topics — mostly because it makes it easier to design school curricula — algebra flows seamlessly from geometry; it is geometry done without pictures, a move that liberates it and allows the mathematics to flourish. To see how, let’s return — as ever, it seems — to the ancient practices of taxation.
As we saw in our look at geometry, taxes were often based on field areas — the Babylonian word for area, eqlum, originally meant ‘field’. It’s no wonder that Babylonian administrators had to learn how to solve puzzles like this one offered up on the ancient Babylonian tablet YBC 6967, which sits in the Yale collection:
The area of a rectangle is 60 and its length exceeds its breadth by 7. What is the breadth?
Let’s try solving it. If the breadth is x, the length is x + 7. The area of a rectangle is simply the breadth multiplied by the length, so the area A is given by this equation:
A = x(x + 7)
The parentheses here tell you to multiply each of the things inside the parentheses by the thing immediately outside it, which leads to:
A = x2 + 7x
The Babylonians would solve this via a series of steps that illustrate the close connection between algebra and geometry. The process is known as ‘completing the square’.
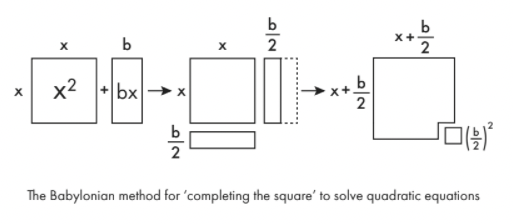
To make an equation of the type x2 + bx manageable, you first draw it as geometrical shapes. x2 is just a square of side x. bx is a rectangle of length x and breadth b. Split that rectangle in two lengthways and move one half to the bottom of the original square, and you can almost make a larger square. To complete that larger square, you just need to add in a tiny square of side b/2. The area of this tiny square is (b/2)2. So you can see that the original expression is actually equivalent to (x + b/2)2 – (b/2)2.
Given an equation of the form
x2 + bx = c
the Babylonians would substitute in the result of completing the square, making it:
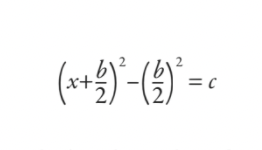
Then they would work this through and reduce it all down to the formula (though it wasn’t written as a formula in the modern sense):
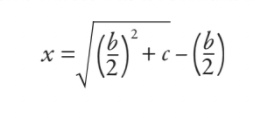
The answer is that the breadth is 5, and the length is 12. But I wonder if that formula looks slightly familiar to you? If I offer you a tweak to the original equation so that you have
ax2 + bx + c = 0
you would solve this using a formula you learned at school — the quadratic formula:
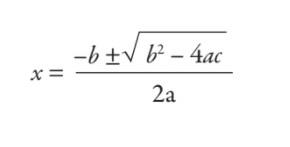
As you can clearly see, what you learned at school is little more than a 5,000-year-old tax calculating tool. None of us grow up to be Babylonian tax officials, though — so why are students learning the quadratic formula these days? It’s a fair question, and one that causes arguments even among maths teachers.