The one cosmic secret that demands a new particle collider

- Ever since antimatter particles were first discovered in the early 20th century, physicists have marveled at the fact that all of the cosmos appears to be made up of matter, with little trace of its antimatter counterpart.
- It isn’t just everything on Earth, but the planets, stars, galaxies, and more that we observe all appear to be made up of matter, with even colliding galaxy clusters showing no evidence that any of their components are made of antimatter.
- But what is the origin of the matter-antimatter asymmetry? How did our Universe come to be predominantly made of matter? It’s one cosmic mystery that a new particle collider could shed more light on than any other approach.
Here in our Universe, there are some cosmic puzzles that loom very large, casting a grand veil of uncertainty over our attempts to understand all of reality. Some of the biggest ones include:
- Why does the Universe obey the rules that it does, as opposed to any other rules?
- Why do the fundamental constants have the values that they do, rather than any other values that they could have taken on?
- Why do the particles of the Standard Model have the masses that they’re observed to have, and why are neutrinos massive at all?
- Why do we have dark matter and dark energy, and what, exactly, are these mysterious forms of energy that have eluded direct detection so far?
Yet there’s one enormous question, of importance on cosmic scales as well as to those who study nature at an elementary level, that often gets overlooked: why is our Universe, and everything in it, predominantly composed of normal matter, and not of antimatter? We’ve learned a whole slew of lessons about the Universe — what makes it up, what the nature of the various particles and antiparticles are, what rules they obey, etc. — and yet we’ve not once concocted a way to change the net number of baryons (things like protons and neutrons) or leptons (things like electrons) in the Universe. Yet, very clearly, the Universe did just this at some point in its distant past, otherwise there wouldn’t be the planets, stars, galaxies, and more that we observe all throughout the Universe.
This longstanding mystery has been unsolved for as long as it’s been noticed, but the best chance we have to make progress is one that most people wouldn’t expect: to build a new, more powerful, more precise particle collider. Here’s the science behind this mystery, and why a new collider is our best bet to try to solve it.
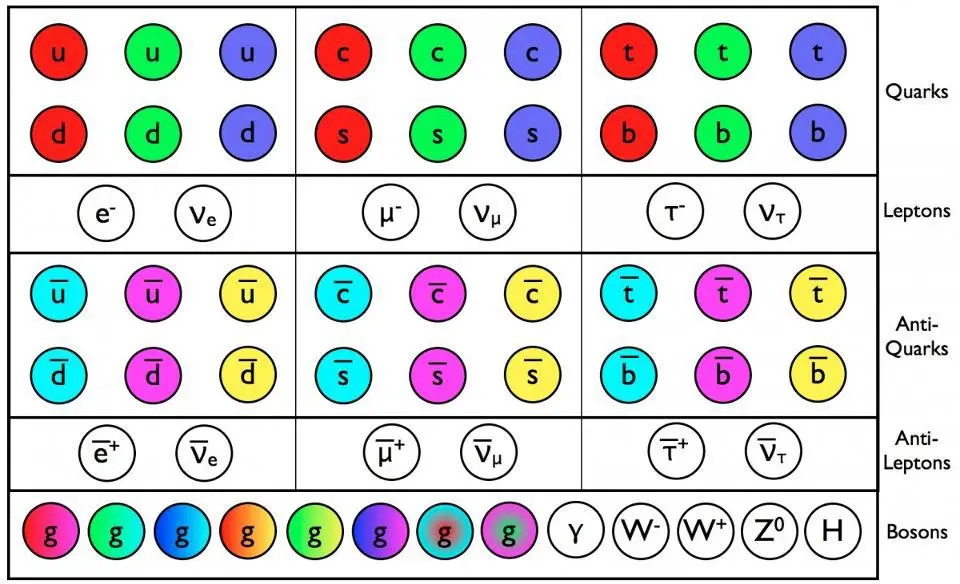
The puzzle itself is quite simple. Here in our Universe, we have the set of fundamental particles whose existence we are certain of: the particles and antiparticles of the Standard Model. They include:
- quarks, which come in the six different flavors of up, down, strange, charm, bottom, and top, which have both electric charges and color charges,
- the antiquarks, which are the antiparticle versions of the quarks, with anti-flavors and anti-colors, as well as opposite electric charges to the quarks,
- the charged leptons, which are the electron, muon, and tau, with an electric charge but no color charge,
- the charged antileptons, which are the antiparticle versions of the electron, muon, and tau, with opposite electric charges to the charged leptons,
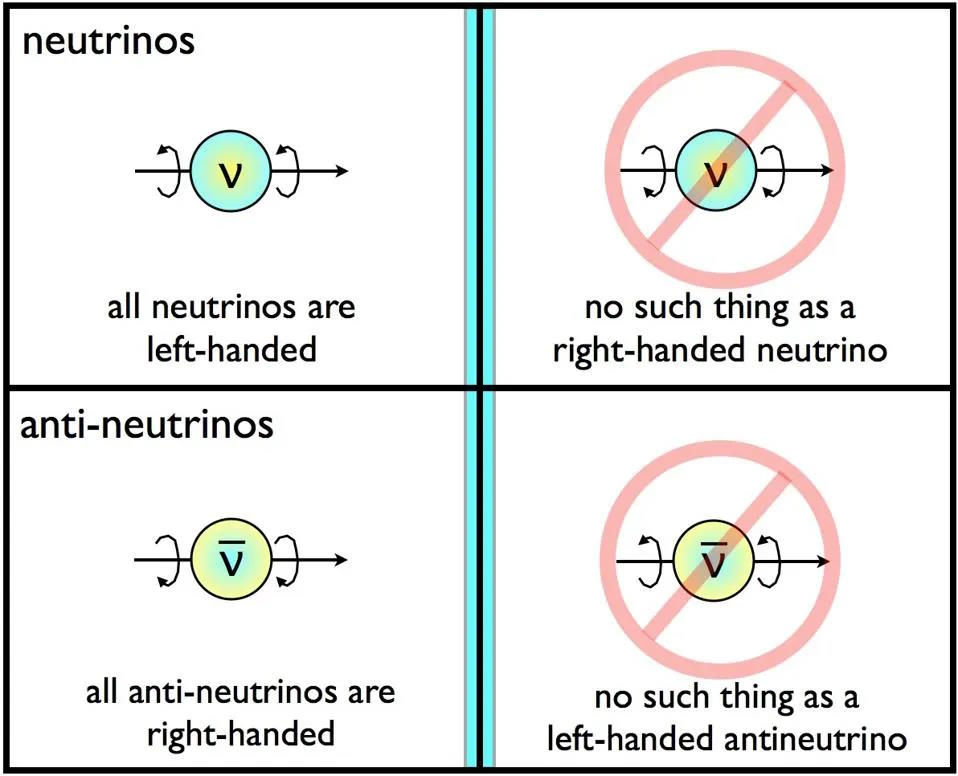
- the neutrinos, which come in three different species and which have a very tiny but non-zero mass, but that have neither color charge nor electric charge, but always have a left-handed helicity,
- the antineutrinos, which also have three different species, tiny and non-zero masses, and also are colorless and electrically neutral, but always have a right-handed helicity,
- as well as the bosons of the Universe, which include the eight gluons that mediate the strong force, the photon that mediates the electromagnetic force, the three heavy weak bosons (the W-and-Z) that mediate the weak interactions, as well as the Higgs boson.
The quarks and leptons make up all the known normal matter in the Universe, while the antiquarks and antileptons have equal and opposite properties and make up antimatter.
If you can make three quarks bind together, you get a baryon: a composite particle that can be stable, such as a free proton or a neutron inside an atomic nucleus. If you can make three antiquarks bind together, you’ll get an antibaryon, such as an antiproton. Both of these types of particles, as well as lepton-antilepton pairs, are frequently created in reactions that occur inside particle accelerators and colliders, as well as from natural high-energy processes, such as collisions with cosmic rays.

Now, here are two facts about the Universe that, while both true, are and should be incredibly unsettling for physicists.
Fact #1: Every reaction we’ve ever created, studied, or measured in particle physics, whether on Earth or in space or anywhere else, has never resulted in a net violation of either baryon number or lepton number. If you create (or destroy) a baryon (or lepton), you also create (or destroy) an equal amount of antibaryons (or antileptons), leaving the total number of net baryons (or leptons) unchanged. The amount of baryons minus the amount of antibaryons, as well as the amount of leptons minus the amount of antileptons, is always the same: before and after any and all reactions or interactions.
Fact #2: But when we look out at the Universe that we have access to, whether we look at
- what’s here on Earth,
- what exists within our Solar System,
- what exists in interstellar space or in star systems found all throughout the Milky Way,
- the other galaxies found all throughout the Universe,
- or even galaxy groups, galaxy clusters, or the grand cosmic web,
we always find the same thing: all of these structures are made exclusively of matter, and not of antimatter. There are no places where matter and antimatter are meeting and annihilating (except as the result of high-energy processes that have produced both matter and antimatter in equal amounts) that shows an interface between a matter-dominated and an antimatter-dominated region of the cosmos. As far as we can tell, all of the Universe, everywhere, is populated with roughly the same amounts of normal matter everywhere, with hardly any antimatter to speak of at all.

This is one of the greatest open questions in all of physics today, and one of the greatest unsolved physics puzzles about our very existence. But for some reason — and even I myself am not sure what the reason is — this grand existential puzzle has fallen out of favor with the general public. While we still ponder great mysteries like dark matter and dark energy, the extremely puzzling unanswered question of how there came to be so much matter (and practically no antimatter) in our Universe is calling out to us to try to solve it. It’s one of the greatest mysteries of all-time, and yet, when physicists talk about the great mysteries of the Universe, this one often simply gets overlooked.
And yet, it turns out the laws of physics aren’t completely, perfectly symmetric between matter and antimatter. Sure, this is true for three out of the four fundamental forces: the gravitational, electromagnetic, and strong nuclear forces don’t discriminate. If you have a charged particle moving through an electric field, interacting with a magnetic field, in the vicinity of another charged particle, or even interacting with light, there’s no difference between the interactions and effects on matter versus antimatter. If that particle (or antiparticle) moves through a gravitational field, interacts with a mass, or experiences the passage of a gravitational wave, there’s also no difference between matter and antimatter. Although it’s far more complicated, the strong nuclear force is no different: quarks bind together to make baryons exactly the same way that antiquarks bind together to make antibaryons, and quark-antiquark combinations (in the form of mesons) can exist with no trouble at all.
But then we come to the weak nuclear interactions, and everything looks different.
We often say, in particle physics, that there are three symmetries worth considering.
- There’s C-symmetry, or charge conjugation symmetry, which replaces all of the charges (electric, color, and even weak isospin and weak hypercharge) inherent to your system with their opposite-charged counterparts, and this is the same, in particle terms, of replacing all of your system’s particles with their antiparticle counterpart, and vice versa.
- There’s P-symmetry, or parity symmetry, which replaces all of your particles (and/or antiparticles) with their mirror-symmetry counterpart. This is the same as reflecting your system in a mirror, and/or replacing notions of “front” with “back” and vice versa, but keeping the other two dimensions (up/down and left/right) the same.
- And there’s T-symmetry, or time-reversal symmetry, which replaces a system which runs forward in time with a system that runs backward in time. It’s as though you change the direction that time runs, and that reverses your T-symmetry.
Now, there’s a famous theorem in physics — the CPT theorem — that demands that the combination of these three symmetries together, or the equivalent of
- changing particles for antiparticles,
- reflecting your system in the mirror,
- and changing the direction that time runs,
all at once always leaves you with a system that behaves identically to your original system. And for three of the fundamental forces (gravitational, electromagnetic, and strong nuclear forces), the C, P, and T symmetries are all conserved individually, as well as together. But for the weak nuclear force, only the combination of C, P, and T, all together, is preserved; each of these symmetries, on its own, is violated by the weak interactions.
It turns out that the weak interactions violate not just each individual symmetry, C, P, and T, but violate the combination of any two symmetries imposed together: CP-symmetry, CT-symmetry, and PT-symmetry. The combination of C and P, for the weak interactions, is a very close call. Weak interactions that are C-symmetry violating do so at the nearly 100% level; C-violation is maximized. Similarly, weak interactions that violate parity, or the P-symmetry, also do so at nearly the 100% level; P-violation is similarly maximized. But when you put these two symmetries together, and create a circumstance where you’ve:
- replaced all the particles with antiparticles (and vice versa),
- and have replaced your original system with the mirror-reflection of that system,
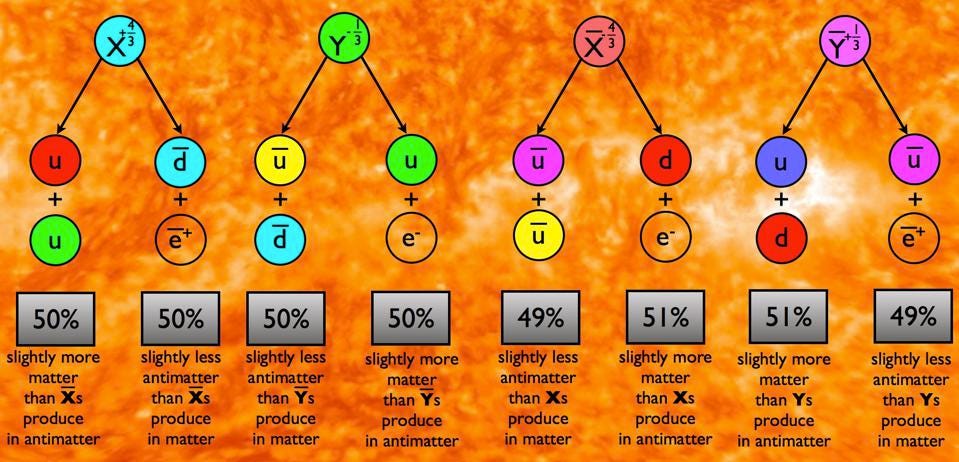
you find that the amount of C-violation and the amount of P-violation don’t cancel each other out, exactly. Instead, there’s a tiny amount of CP-violation as well, where about 1-in-1000 particles (versus antiparticles reflected in a mirror) will behave differently. This is just a ~0.1% violation of the CP-symmetry, but it turns out to be incredibly important from a cosmic point of view.
You see, we might not know exactly how the Universe came to possess more matter than antimatter, or why it has the properties that we observe it to have today. But we do know an awful lot about the Universe’s past, and one of the things we’ve learned — in general, at least — is what is required to create a matter-antimatter asymmetry from a state where none existed previously. CP-violation, it turns out, is one of the key ingredients.

That’s because there are three conditions that, if you combine them all together, will make baryogenesis — or the creation of a matter-antimatter asymmetry from an initially matter-antimatter symmetric state — not just possible, but inevitable. These conditions were worked out in the late 1960s by Soviet physicists Andrei Sakharov, where the three Sakharov conditions are:
- out-of-equilibrium conditions, such as an expanding and cooling Universe that began with a hot Big Bang,
- the presence of both C-violating and CP-violating interactions,
- and the admissibility of baryon-number-violating interactions.
Now, you might look at these three things, and have no problem with items #1 and #2, as the Universe seems to give us both of those in abundance.
Not only is the expanding Universe an out-of-equilibrium system, but it is perhaps the single most out-of-equilibrium system ever imagined. Things that are permitted and ubiquitous at high energies and early times are highly suppressed and outright forbidden at later times and under lower-energy conditions. C-violation and CP-violation is copious in the weak interactions, and can affect a great number of baryons and mesons that contain strange, charm, or bottom quarks and/or antiquarks. (It is suspected, but not proven, that this may occur for top-containing or even some down-containing particles or antiparticles, as well.)
Still, we’ve never observed a baryon-number-violating interaction. However, this isn’t impossible; even within the Standard Model alone, there’s a type of interaction that can do it: the sphaleron process.
Strictly speaking, the Standard Model doesn’t conserve baryon number and lepton number individually, but only the difference between them: the baryon number minus the lepton number. In a practical sense, this can convert:
- three baryons into three antileptons,
- three antibaryons into three leptons,
- three leptons into three antibaryons,
- or three antileptons into three baryons,
and so on. As long as the net number of baryons added/subtracted and the net number of leptons added/subtracted are equal and come in multiples of three, this is allowed under the proper conditions within the Standard Model: either at very high energies or, even though this process would be suppressed at lower energies, through quantum tunneling.
That’s the first motivation for why we should build a higher-energy collider. Although this process is estimated to take place at approximately an energy of around 10 TeV, that’s the energy requirement per particle for this interaction to occur. With a combined center-of-mass energy of 14 TeV for the Large Hadron Collider, this threshold is not achieved, and no sphaleron processes (and hence, no baryon-violating interactions) can occur. With a larger, more powerful collider — for example, a proton-proton collider that can achieve 100 TeV of center-of-mass energy — this would finally be accessible, and we could see our very first baryon number-violating interaction directly. It would be a huge achievement for physics, and for answering a vital existential question: the one about how the very stuff we’re made out of, atoms, came to exist (over antiatoms) in our Universe.
Even with this huge carrot dangling in front of us of creating more baryons than antibaryons (and, simultaneously, the ability to generate more leptons than antileptons), that’s not necessarily “the big prize” in terms of baryogenesis. It turns out that there’s an even deeper motivation for studying this puzzle at a next-generation collider. Sure, seeing baryon number-violating interactions (and lepton number-violating interactions as well) would be revolutionary, and would easily be one of the biggest discoveries in physics of all-time. But could the baryon violation generated by sphalerons in the Standard Model explain the matter-antimatter asymmetry present in the Universe today?
It could, but only if a certain scenario is true.
We’ve learned that there’s an electroweak symmetry associated with the Standard Model: a symmetry that’s restored at high energies and at early times in our Universe, but a symmetry that breaks as the Universe cools through the electroweak phase transition. If the nature of the transition is first-order, which means it gets caught in a false minimum and quantum tunnels into the true minimum, it could indeed explain how our Universe got its current matter-antimatter asymmetry. However, if the transition is second-order — which is what’s predicted by the Standard Model alone, by the way — this cannot be the full explanation on its own. Some other component or ingredient must be at play.
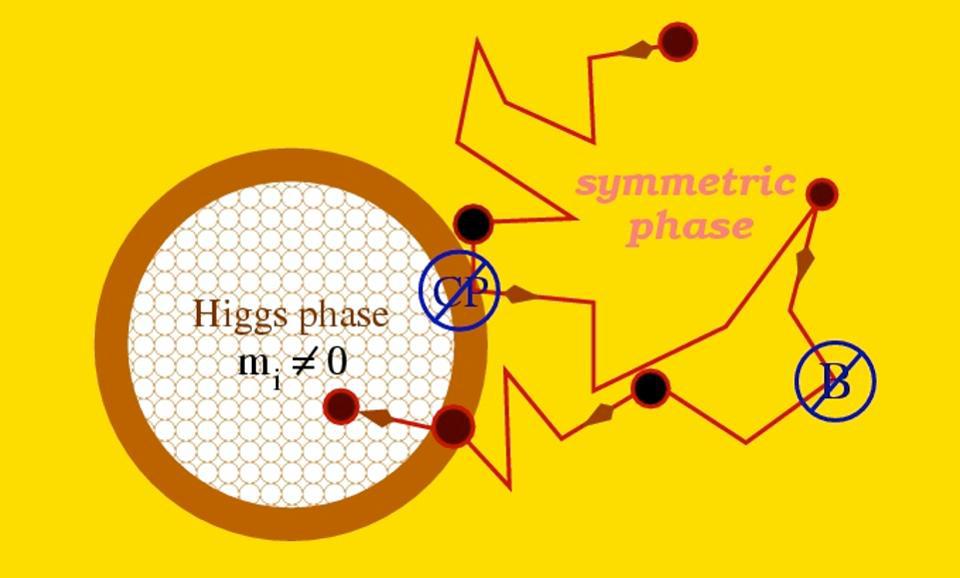
But we already know that the Standard Model cannot be all there is; something else must exist to explain dark matter and several other cosmic puzzles that stymie us today. If one of the other “things” out there has the same quantum numbers as the Higgs — such as a second Higgs doublet, for one example — then that can mix with the already-discovered Higgs to alter the shape of the phase transition. Even if that second doublet is at much higher energies, even if it’s out of reach of the LHC or even a proposed future collider, the effects it has on the electroweak phase transition can still render it strongly first-order, as opposed to the second-order transition predicted by the Standard Model alone.
If we want to know whether baryon number-violating interactions exist, as predicted by the Standard Model, a next-generation particle collider is an essential tool. If we want to probe the nature of the electroweak phase transition and find out whether it’s first-order or second-order, a next-generation particle collider is the tool we need for that job. And if we want to determine whether the matter-antimatter asymmetry that exists within our Universe was created during the electroweak phase transition long ago in our cosmic past, a next-generation particle collider is arguably the only tool that can reveal the answer to that question. It’s the one cosmic secret that absolutely demands that we build a next-generation collider if we hope to find the answer.