Does the Universe expand by stretching or creating space?
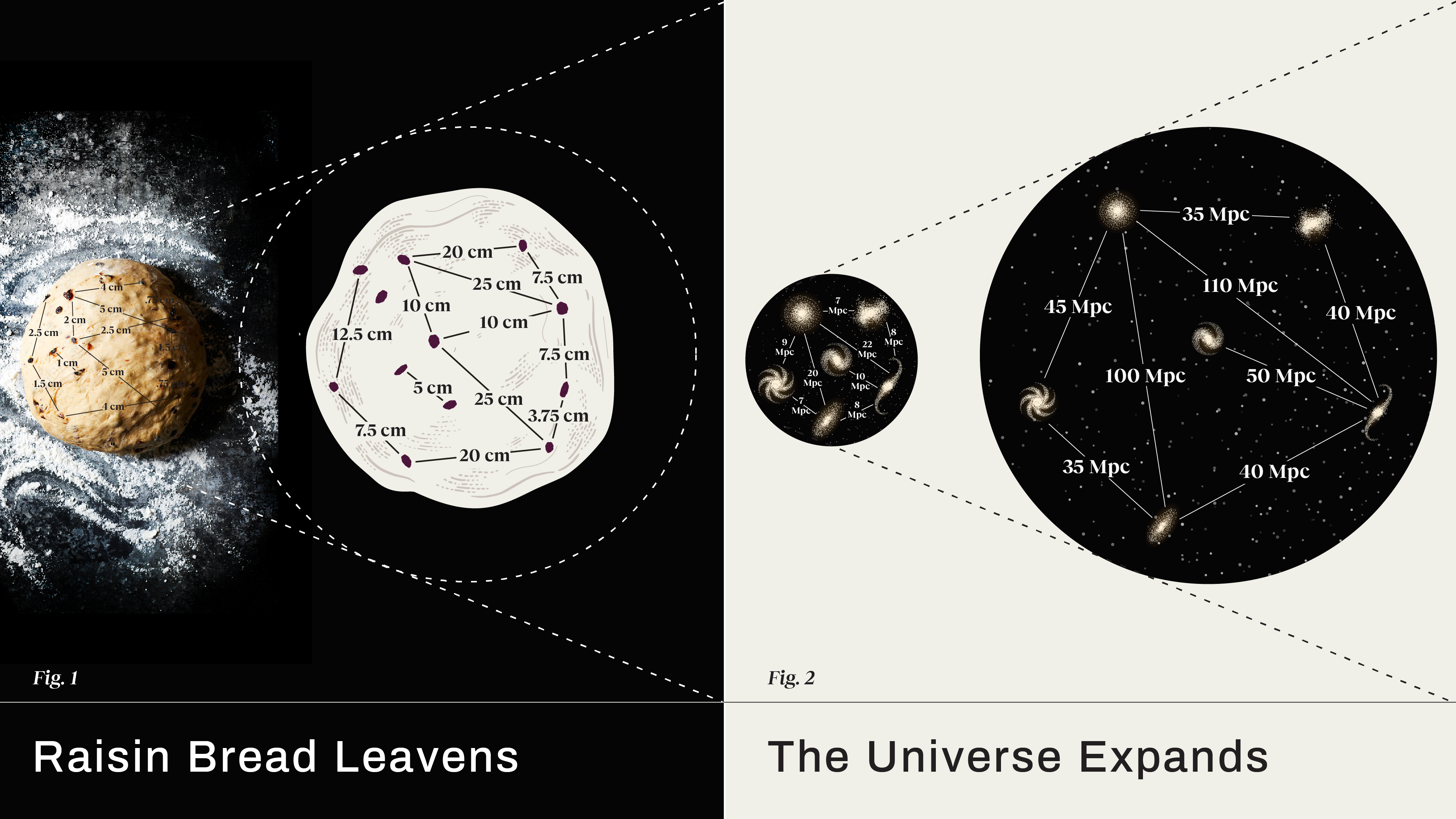
- The farther away we look in the Universe, the greater the amount that light, gravitational waves, and all signals are lengthened and dilated (or “redshifted”) by the expansion of space.
- This effect applies to all observations of objects beyond our own Local Group, but how, exactly, does space itself actually expand: by stretching, or by the creation of new space in the “gaps” opened up by cosmic expansion?
- The surprising answer is that both interpretations have their usefulness, but both analogies are fundamentally limited and will fail if you use them incorrectly. The expansion of the Universe is real, but no one analogy is perfect.
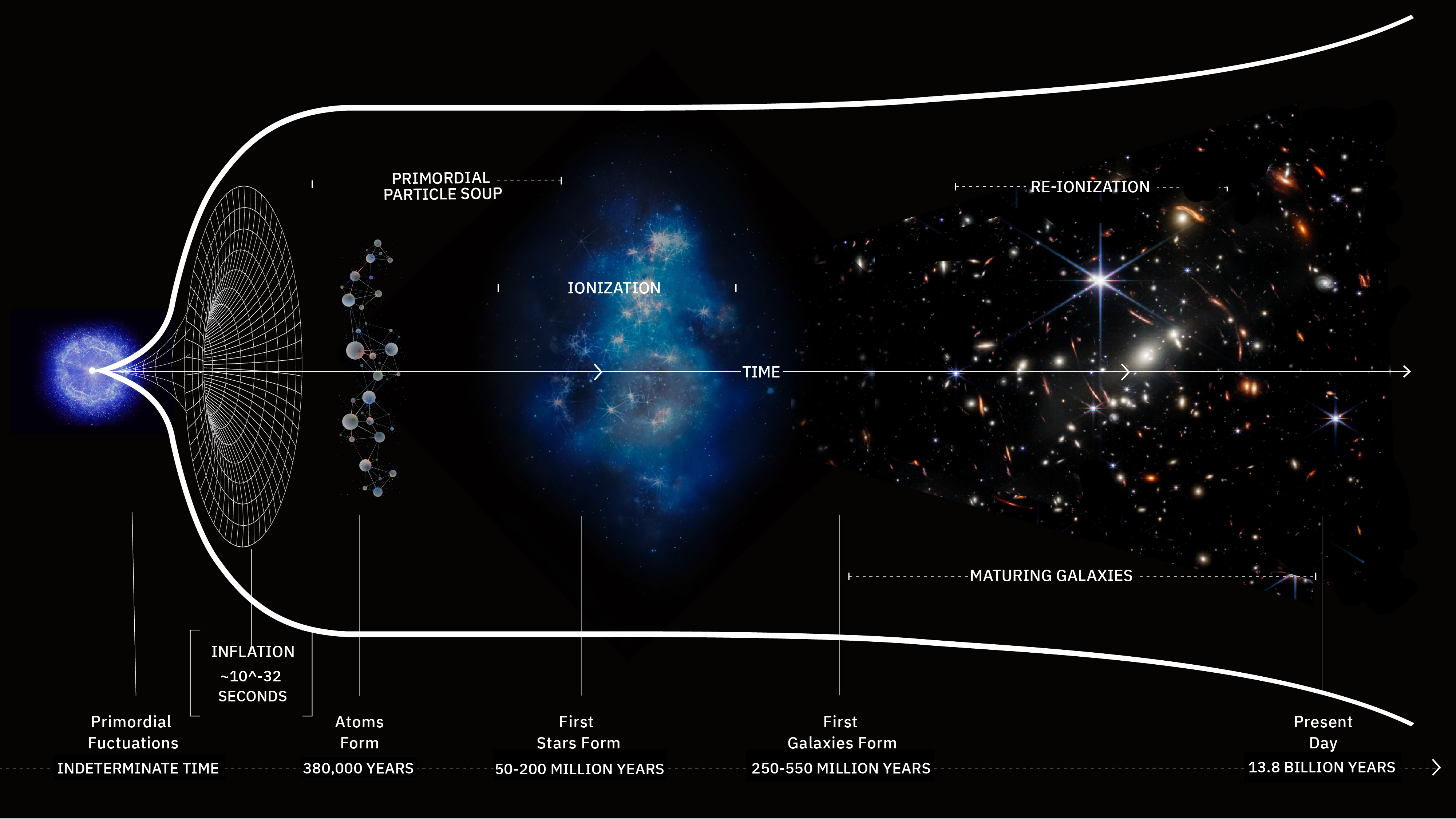
It’s been almost 100 years since humanity first reached a revolutionary conclusion about the nature of our Universe: space itself cannot and does not remain static, but rather evolves with the passage of time. One of the most unsettling predictions of Einstein’s general relativity is that any Universe — so long as it’s uniformly (or almost uniformly) filled with one or more species of matter, radiation, or energy — cannot remain the same over time. Instead, it must either expand or contract, something initially derived independently by three separate people: Alexander Friedmann (1922), Georges Lemaitre (1927), and Howard Robertson (1929), and was later generalized by Arthur Walker (1936).
Right at around the same time, starting in 1923, observations began to show that the spirals and ellipticals in our sky were actually galaxies: “island universes” that were well outside of our own Milky Way. With new, more powerful measurements, we could determine that the farther away a galaxy was from us, the greater the arriving light in our instruments was redshifted, or observed at longer wavelengths, compared to the light that was initially emitted. It was as though the very act of journeying through space altered the wavelength of that traveling light.
But what, exactly, happens to the fabric of space itself while this process occurs? Is the space itself stretching, as though it’s getting thinner and stretched out? Is more space constantly being created, as though it were “filling in the gaps” that the expansion creates? This is one of the toughest things to conceive of in modern astrophysics. If we think hard about it, however, we’re capable of wrapping our heads around it. Let’s explore what’s going on.

The starting point of our conversation has to be general relativity: our modern theory of gravity first put forth by Einstein. General relativity, at its core, is a framework that relates two things that might not obviously be related:
- the amount, distribution, and types of energy — including matter, antimatter, dark matter, radiation, neutrinos, and anything else you can imagine — that are present all throughout the Universe,
- and the geometry of the underlying spacetime, including whether and how it’s curved and whether and how spacetime itself will evolve.
If we inhabited a completely empty Universe, or a Universe that contains nothing within it at all — no matter, radiation, or energy of any form — you’d get the flat, Newtonian-like space you’re intuitively used to: something that’s static, uncurved, and unchanging.
But what if we then considered the absolute simplest case of a non-empty Universe? If, instead, we were to put down a point mass in the Universe, we’d find out that space was curved in a particular way: Schwarzschild space. Any “test particle” that we’d put down onto our Universe would be compelled to flow toward that mass, following a particular trajectory.
And if we were to then make our physical situation just a little bit more complicated, by putting down a point mass that also rotates, we’d get space that’s curved in a more complex way: according to the rules of the Kerr metric. It will have an event horizon, but instead of a point-like singularity, the singularity will get stretched out into a circular, one-dimensional ring. Again, any “test particle” you put down will follow the trajectory laid out by the underlying curvature of space.

These spacetimes are clearly much more complicated than a spacetime that’s simply flat. However, they are still “static” in the sense that any distance scales you might include or measure — like the size of the event horizon or the distance between two arbitrary points within this spacetime — don’t change over time. If we could somehow “exit” a Universe with this spacetime and return to it later, whether a second, an hour, or a billion years later, the structure of this spacetime would be identical, irrespective of when we returned to it. In spacetimes like these, there’s no cosmic expansion that’s present. There’s no change in the distance or the light-travel-time between any points within this spacetime. With just one (or fewer) sources of matter inside, and no other forms of energy, these “model Universes” really can be static.
But it’s a very different game when you choose not to put down isolated sources of mass or energy, but instead to fill your Universe, uniformly, with “stuff” everywhere. In fact, the two criteria we normally assume about our Universe, and which are strongly validated by large-scale observations, are called isotropy and homogeneity.
- Isotropy tells us that the Universe is the same in all directions: everywhere we look on cosmic scales, no “direction” looks particularly different or preferred from any other.
- Homogeneity, on the other hand, tells us that the Universe is the same in all locations: the same density, temperature, and expansion rate exist to better than 99.99% precision on the largest scales.
As far as we can tell, our Universe, on large cosmic scales, is indeed both isotropic and homogeneous.

In this case, having a Universe that’s uniformly filled with some sort of energy (or multiple different types of energy), the rules of general relativity not only mandate that the Universe must evolve, they tell us how. The equations that govern the evolution of the Universe are known as the Friedmann equations: derived by Alexander Friedmann all the way back in 1922, a year before we even discovered that the largest, most prominent spiral in the sky — the great nebula in Andromeda — was actually a galaxy outside of and beyond the Milky Way. (In short order, we extended that knowledge to practically all the spiral and elliptical nebulae known.)
The spacetime fabric of the Universe, if it’s uniformly filled with one or more types of matter and/or energy, must expand or contract according to these equations. The mathematics tells us, with no ambiguity, that this must occur.
But what, exactly, does “expansion” or “contraction” actually mean when it comes to space itself?
You see, space itself is not something that’s directly measurable. It’s not like we can go out and take some space and just perform an experiment on it. Instead, all we can do is observe the effects of space on observable things — like matter, antimatter, and light — and then use that information to figure out what the underlying space itself must be doing to cause those effects.

For example, if we go back to the black hole example (although it applies to any mass), we can calculate how severely space is curved in that black hole’s vicinity. If the black hole is spinning, we can calculate how significantly space is “dragged” along with the black hole due to the presence of the black hole’s angular momentum. If we then measure what happens to objects in the vicinity of those objects, we can compare what we see with the predictions of general relativity. In other words, we can actually perform experiments to determine whether space curves in the way Einstein’s theory tells us it ought to in a wide variety of ways. As soon as the first conflict arises — as soon as a single observation is inconsistent with Einstein’s predictions — we will have a compelling case for extending the theory of gravity beyond Einstein’s general relativity.
But that day, a full 109 years after general relativity was first put forth, has not yet arrived. To an incredible level of precision, every observation matches and agrees with general relativity’s predictions. Light blueshifts when it enters an area of extreme curvature and redshifts when it leaves. This gravitational redshift has been measured for stars orbiting black holes, for light traveling vertically in Earth’s gravitational field, from the light coming from the Sun, and even for light passing through growing galaxy clusters. It’s also been measured right here on Earth, as light redshifts when it travels upward in Earth’s gravitational field, and blueshifts when it travels downward, closer to Earth’s center.
Similarly, other predictions such as:
- gravitational time dilation,
- the bending of light by large masses,
- and the precession of everything from planetary orbits to rotating spheres sent up to space,
have all spectacularly agreed with Einstein’s predictions.

But what about the Universe’s expansion? When we think about the expanding Universe scientifically, the question we should be asking ourselves is: “What, observably, is changing about the things we’re capable of measuring in the Universe?” After all, that’s what we can physically predict, that’s what’s physically observable, and that’s what will inform us as to what’s actually physically occurring. Anything else is us placing a veneer — a mask reflecting the limits of our own intuition — atop what we actually understand about reality.
The simplest evolving quantity we can consider in an expanding Universe is density. If our Universe is filled with “stuff,” then as the Universe expands, the volume of the space that this ”stuff” occupies will increase.
We normally think about matter as the “stuff” we’re thinking about. Matter is, at its simplest level, a fixed amount of massive “stuff” that lives within space. As the Universe expands, the total amount of stuff remains the same, but the total amount of space for the stuff to live within increases. For matter, density is just mass divided by volume, and so if your mass stays the same (or, for things like atoms, if the number of particles stays the same) while your volume grows, your density should go down. When we do the general relativity calculation, that’s exactly consistent with what we find for matter.
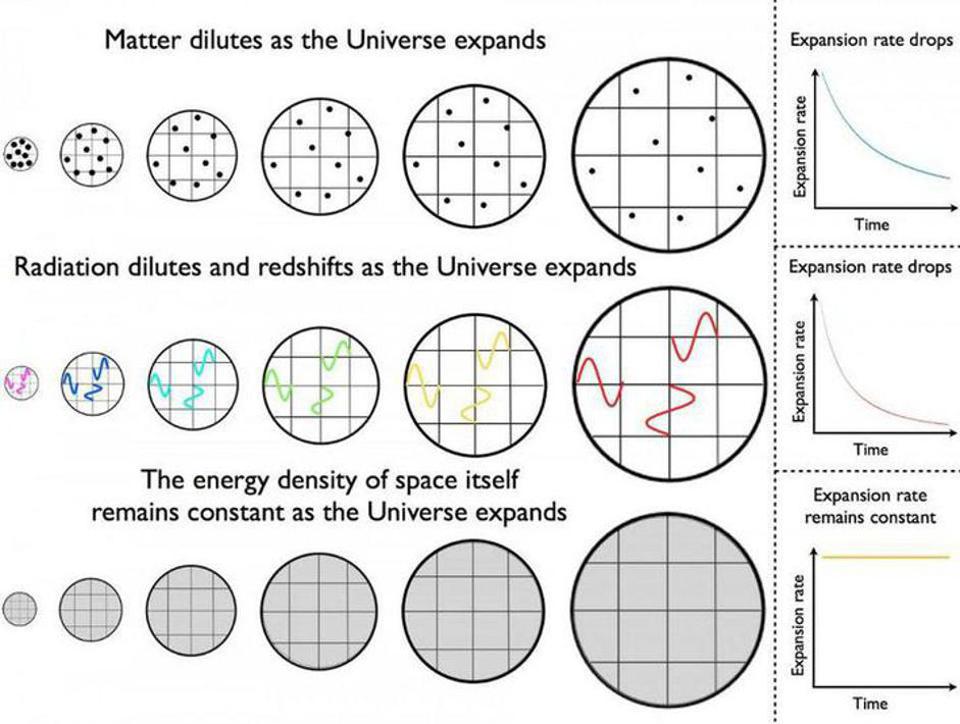
But even though we have multiple types of matter in the Universe — normal matter, black holes, dark matter, neutrinos, etc. — not everything in the Universe is matter.
For example, we also have radiation: quantized into individual entities, like matter, but massless, and with its energy defined by its wavelength. As the Universe expands, and as light travels through the expanding Universe, not only does the volume increase while the number of particles remains the same, but each quantum of radiation experiences a shift in its wavelength toward the redder end of the spectrum: longer wavelengths. This redshifting effect is how the expanding Universe was first detected, and shows up in every galaxy and quasar we measure beyond our own Local Group.
Meanwhile, our Universe also possesses dark energy, which is a form of energy that isn’t in the form of particles at all, but rather appears to be inherent to the fabric of space itself. While we cannot measure dark energy directly the same way we can measure the wavelength and/or energy of photons, there is a way to infer its value and properties: by looking at precisely how the redshifting light from distant objects evolves as a function of distance. Remember that there’s a relationship between the different forms of energy in the Universe and the expansion rate. When we measure the distance and redshift of various objects throughout cosmic time, they can inform us as to how much dark energy there is, as well as what its properties are. What we find is that the Universe is about ⅔ dark energy today, and that the energy density of dark energy doesn’t change: as the Universe expands, the energy density remains constant.

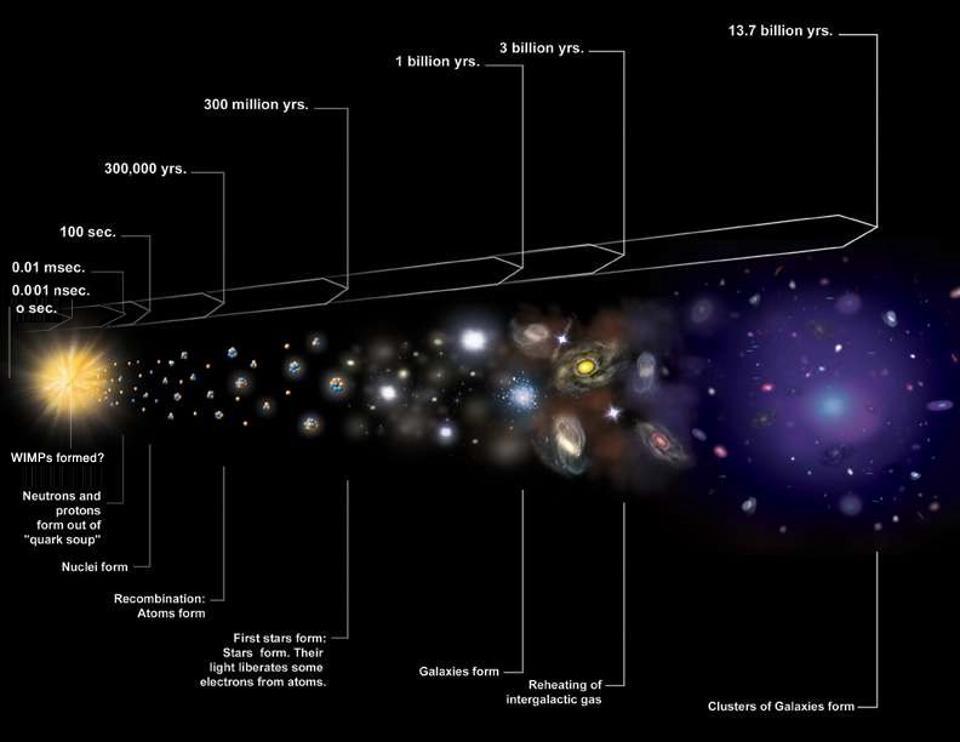
When we put the full picture together from all the different sources of data that we have, a single, mostly consistent picture emerges. Our Universe today is expanding at somewhere around 70 km/s/Mpc, which means that for every megaparsec (about 3.26 million light-years) of distance an object is separated from another object, the expanding Universe contributes a redshift that’s equivalent to a recessional motion of 70 km/s.
That’s what it’s doing today, mind you. But by looking to greater and greater distances and measuring the redshifts there, we can learn how the expansion rate differed in the past, and hence, what the Universe is made of: not just today, but at any point in history. Today, our Universe is made of the following forms of energy:
- about 0.008% radiation in the form of photons, or electromagnetic radiation,
- about 0.1% neutrinos, which now behave like matter but behaved like radiation early on, when their mass was very small compared to the amount of (kinetic) energy they possessed,
- about 4.9% normal matter, which includes atoms, plasmas, black holes, and everything that was once made of protons, neutrons, or electrons,
- about 27% dark matter, whose nature is still unknown but which must be massive and clumps, clusters, and gravitates like matter,
- and about 68% dark energy, which behaves as though it’s energy inherent to space itself.
If we extrapolate backward, based on what we infer about today, we can learn what type of energy dominated the expanding Universe at various epochs in cosmic history.

Notice, very importantly, that the Universe responds in a fundamentally different way to these differing forms of energy. When we ask, “What is space doing while it’s expanding?” we’re actually asking which description of space makes sense for the phenomenon we’re considering. If you consider a Universe filled with radiation, because the wavelength lengthens as the Universe expands, the “space stretches” analogy works very well. (If the Universe were to contract instead, “space compresses” would explain how the wavelength shortens, and energy increases, equally well.)
On the other hand, when something stretches in a conventional fashion, it thins out, just as when something compresses, it thickens up. This is a reasonable line of thought for describing the behavior of light and other forms of radiation, but not for dark energy, or any form of energy intrinsic to the fabric of space itself. When we consider dark energy, the energy density always remains constant. As the Universe expands, its volume is increasing while the energy density doesn’t change, and therefore the total energy increases. From the perspective of dark energy, it’s as though new space is getting created due to the Universe’s expansion.
Neither explanation works well universally: it’s that one explanation succeeds at explaining what happens to radiation (and other energetic particles) while the other works to explain what happens to dark energy (and anything else that’s an intrinsic property of space, or a quantum field coupled directly to space) as the Universe either expands or contracts.

Space, contrary to what you might think, isn’t some measurable, physical substance that you can treat the same way you’d treat particles or some other form of energy that would appear inside a detector. Instead, space is simply the backdrop — a stage, if you will — against or upon which the “play” of the Universe unfolds. We can use the measurements of particles and quanta we can detect from all over the Universe to infer the properties of space, and under the rules of general relativity, if we can know what’s present within that space, we can predict how space will curve and evolve. That curvature and that evolution will then determine the future trajectory of every quantum of energy that exists, including all the quanta we’re capable of detecting.
All of the radiation within our Universe, including every gravitational wave, behaves as though space is stretching, although space itself isn’t getting any thinner. The dark energy within our Universe behaves as though new space is getting created, although there’s nothing we can measure to detect this creation. In reality, general relativity can only tell us how space behaves, evolves, and affects the energy within it; it cannot fundamentally tell us what space actually “is” in a philosophical sense.
In our attempts to make sense of the Universe, we must recognize that there is no justification to adding extraneous structures atop what is measurable. Space neither stretches nor gets created, but simply is as Einstein’s theory describes it. At least, within the context of general relativity, we can accurately learn “how” it is, even if the information of precisely “what” it is lies beyond the realm of science at present.