Could This 40 Year Old Formula Be The Key To Going Beyond The Standard Model?

Why are the rest masses of fundamental particles related like this?

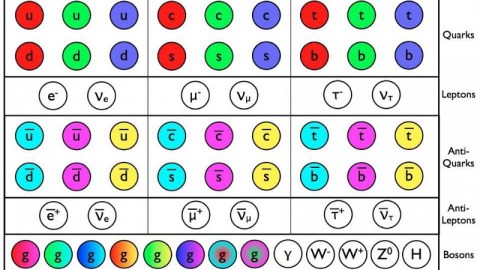
When it comes to the nature of matter in the Universe, the Standard Model describes the known elementary particles perfectly well and without exception, at least so far. There are two classes of fundamental particles:

• the fermions, which all possess non-zero rest masses, half-integer spins, and can be charged under the strong, electromagnetic, and weak interactions,
• and the bosons, which can be massive or massless, possess integer spins, and mediate the strong, electromagnetic, and weak interactions.

The fermions come in three generations and are split between the six types of quarks and leptons, while among the bosons, there are no generations, but merely different numbers of them, depending on the nature of the force being mediated. There’s just one boson (the massless photon) for the electromagnetic force, three (the massive W-and-Z bosons) for the weak force, eight (massless gluons), and one (massive) Higgs boson.

All told, the Standard Model provides the framework for all of the known and discovered fundamental particles, but has no way of providing expected values for what masses each particle should possess. In fact, of the fundamental constants needed to describe our Universe, a full 15 of them — more than half — belong to the rest masses of these particles. And yet, a very simple formula appears to relate many of them to one another, with no explanation as to why. Here’s the puzzling story of the Koide formula.

The early 1980s were an extremely successful time for particle physics. The final pieces of the Standard Model had recently been put into place, with the Higgs mechanism, electroweak symmetry breaking, and asymptotic freedom having all been worked out theoretically. On the experimental side, the advent of powerful new colliders had recently revealed the τ (tau) lepton as well as the charm and bottom quarks, providing empirical evidence for a third generation of particles. With the Main Ring running at Fermilab and the Super Proton Synchrotron collecting the data that would lead to the discovery of the W-and-Z bosons in 1983, the Standard Model was nearing completion.

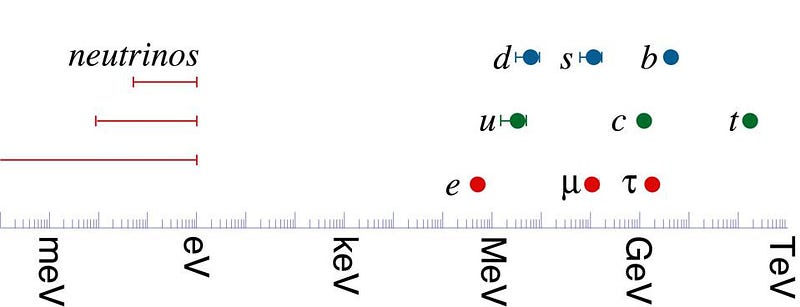
The quarks are only observable indirectly: as parts of bound states making up mesons (quark-antiquark pairs), baryons (three-quark combinations), and anti-baryons (three-antiquark combinations), requiring a sophisticated theoretical toolkit to extract their rest masses. The leptons, however, are observable directly, and their rest masses were easily reconstructed from the energy and momenta of their decay products. For the three charged leptons, their masses are:

• electron: 511 keV/c²,
• muon: 105.7 MeV/c²,
• tau: 1.777 GeV/c².

It might appear, on the surface, that there’s no relationship between these three masses, but in 1981, physicist Yoshio Koide suggested that there might be one, after all.

The electron is the lightest charged particle in the Standard Model, and the lightest of all massive particles except for the neutrinos. The muon, its heavier cousin, is identical in terms of electric charge, spin, and numerous other quantum properties, but its mass is ~207 times greater, and it’s fundamentally unstable, with a mean decay lifetime of ~2.2 microseconds. The tau — the third-generation counterpart of the electron and muon — is similar but even heavier and shorter lived, with a mass that’s about 17 times the muon’s mass and a mean lifetime of just ~290 femtoseconds, surviving less than one-millionth the amount of time a muon lives for.

No relation, right?

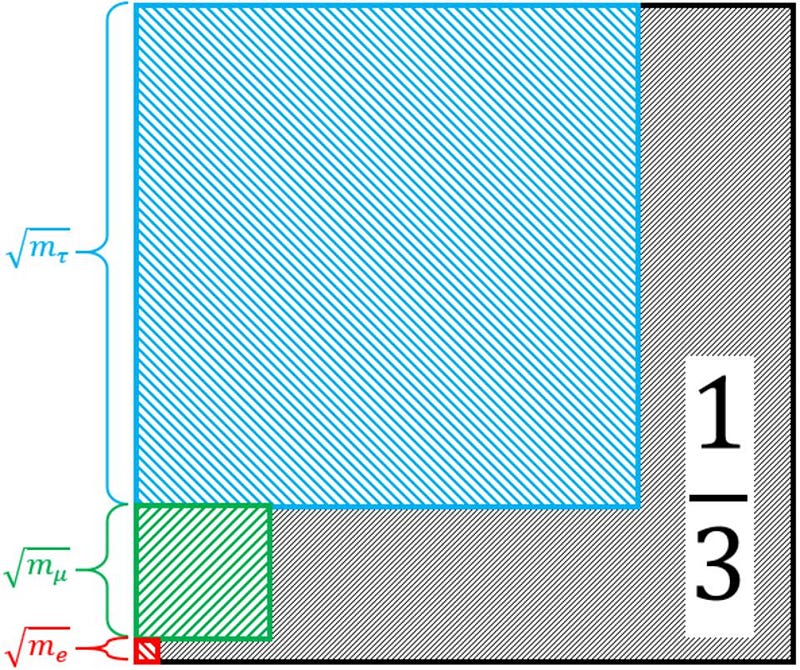
That’s where Koide came in. Perhaps it’s just a numerical coincidence, but it’s well known — at least, in quantum physics — that whenever two particles have identical quantum numbers, they’re going to mix together at some level; you’ll have a mixed state instead of a pure state. Although this isn’t necessarily applicable to the masses of the charged leptons (or any particles at all), it’s a possibility that might be worth exploring. And it’s that same mathematical structure that Koide leveraged when he proposed a very simple formula:

• that if you add the three relevant masses together,
• and divide their sum by the square of the sum of their square roots,
• you get a simple constant out,

which mathematically must lie between ⅓ and 1. In the case of these charged leptons, it just happens to itself be a simple fraction: ⅔, almost exactly.

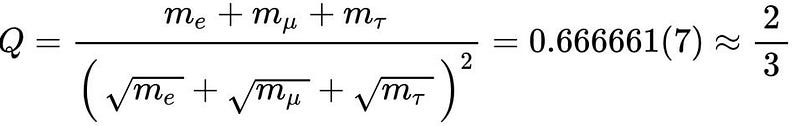
Now, there are many, many relations that one can cook up between various numbers or values that aren’t actually representative of an underlying relationship, but merely appear as a numerical coincidence. In the early days, people thought the fine-structure constant might be exactly equal to 1/136; a little later, that was revised to 1/137. Today, however, it’s measured to be 1/137.0359991, and it’s known to increase in strength at higher energies: up to ~1/128 at electroweak scales. Plenty of suggestive, tantalizing relationships have turned out to be nothing more than coincidences.

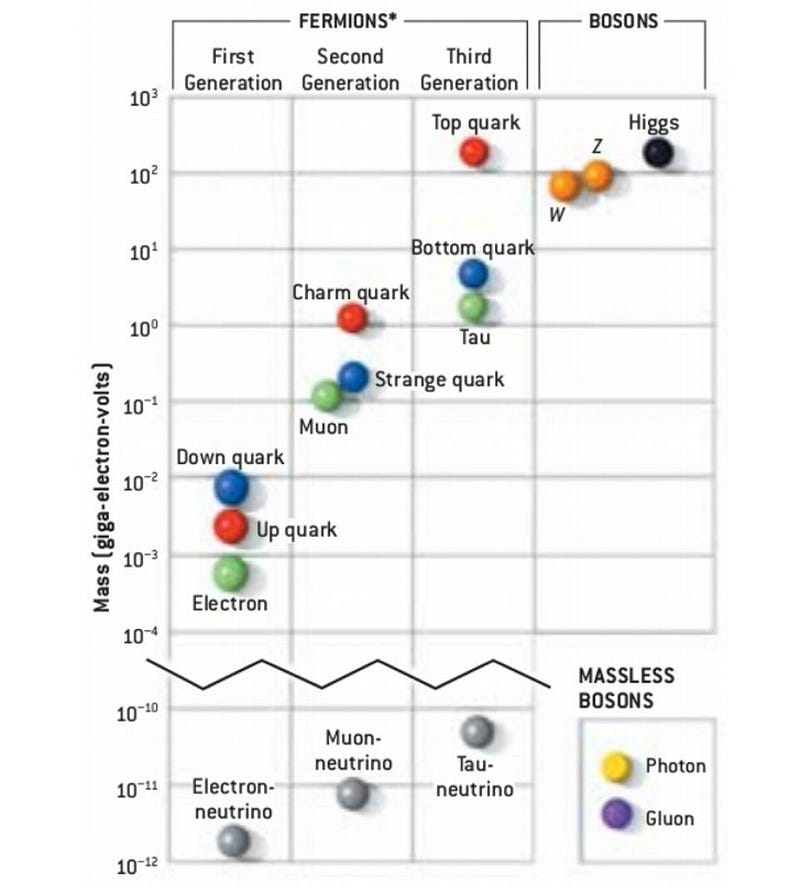
And yet, we have precisely measured values for not only the charged leptons, but for each of the quarks as well: the up, down, strange, charm, bottom, and top quarks. The first three are the lightest quarks, the latter three are the heaviest quarks. Using the best data presently available, their masses (shown without uncertainties) are:

• up: 2.32 MeV/c²,
• down: 4.71 MeV/c²,
• strange: 92.9 MeV/c²,
• charm: 1.28 GeV/c²,
• bottom: 4.18 GeV/c²,
• and top: 173.0 GeV/c².

Interestingly enough, we can attempt to apply the Koide formula to these six masses — in two separate groupings — to see what comes out.

Remarkably enough, for the up, down, and strange quarks, you get a value of approximately 0.562, which is very close to another simple fraction: 5/9, or 0.55555…, and is allowable within the published uncertainties.

Similarly, we can do a comparable analysis for the charm, bottom, and top quarks together as well, yielding a value of 0.669, which is again very close to a simple fraction of 2/3: 0.666666…, with the exact value, again, allowed within the published uncertainties.

And, if we wanted to be extremely bold, we could move over to the bosons, and check out what the relationship is between the only three massive bosons we have:

• the W boson: 80.38 GeV/c²,
• the Z boson: 91.1876 GeV/c²,
• and the Higgs boson: 125.35 GeV/c².

Applying the same formula to these three masses yields a value of 0.3362, which appears to be consistent with a simple fraction of 1/3: 0.33333…, which once again seems like a remarkable, almost-perfect coincidence, although in this case, the errors are small enough that the exact relationship cannot be saved.

It’s important to recognize that these values are only for the “pole” masses, which is the equivalent of “rest mass” in relativity. In quantum physics, the only measurements you can make are based on interactions between various quanta, and those interactions always occur at a particular energy that’s greater than zero. However, by appropriately applying the correct theoretical techniques, you can disentangle what the pole mass is from the inferred mass that your measurements give you. While the measured masses will change — or “run” — with increased energy, the zero-energy limit remains the same.

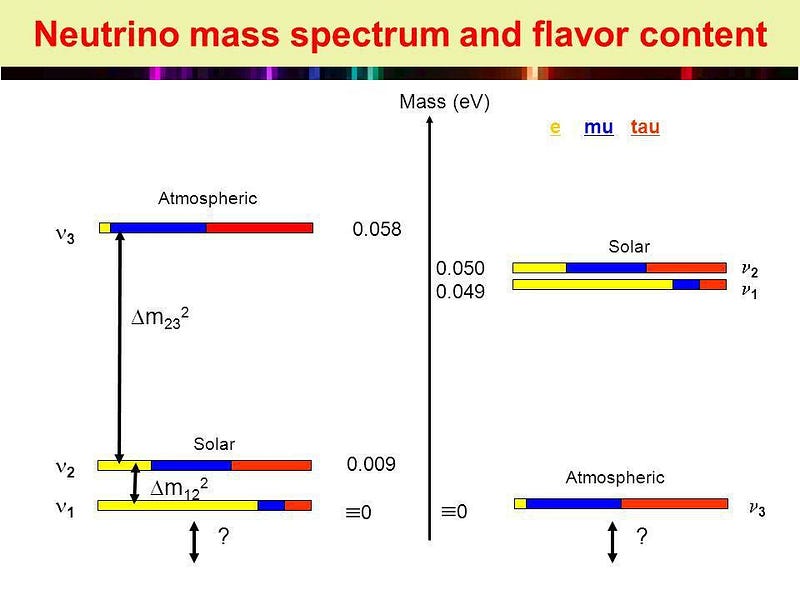
In fact, although the uncertainties in the measured values of neutrino masses has only yielded constraints on their masses, with everything dependent on the yet-unmeasured particulars of how the various neutrino states mix together, there is reason to believe that there exists some sort of hierarchy between the mass states of the three different types of neutrinos: electron, muon, and tau. It’s eminently possible, once those masses can be inferred, that they will also yield an interesting and simple value for the Koide formula.

There have also been attempts to extend the Koide formula in various ways, including to all six quarks or leptons simultaneously, with varying successes: you can get a simple relationship for the quarks, but not for the leptons. Others have tried to tease out deeper mathematical relationships that could underpin the rest masses of the fundamental particles, but at this point, these relationships were only knowable after-the-fact, and could not have been used to accurately predict any unknown masses at any point in time.

However, these patterns most definitely persist across applications, from the charged leptons to the light quarks to the heavy quarks to, quite possibly, the massive bosons and the neutrinos as well. It leads to a remarkable question whose answer is not yet known: is the Koide formula something of great importance, and does it provide a hint of some novel structure that might underlie some property of nature that the Standard Model cannot explain? Or, alternatively, is it simply a combination of numerical coincidence (or worse, a near-coincidence) and the human penchant for seeing patterns, even where none exist?

This latter option should be seriously taken into account before we over-invest in this idea. The fine-structure constant is just one example of a numerical relationship that looks promising when you look at it coarsely, but falls apart when you look at things in greater detail. Early attempts at using quark mixing properties to predict the masses of the top quark gave an initial estimate of ~14 GeV/c² as the mass, whereas its actual mass turned out to be more than 12 times as large as that value.

A little over a decade ago, an attempt was made to use asymptotically safe gravity to predict the mass of the Higgs boson, a few years before it was actually discovered at the Large Hadron Collider. The prediction was astonishingly precise: a mass of ~126 GeV/c², with an uncertainty of just ~1–2 GeV/c² in that energy. When the actual discovery was announced, with a value of ~125 GeV/c², it seemed to vindicate the calculation, but there was a catch: in the intervening time, a number of parameters in the Standard Model were better measured, and that asymptotically safe calculation instead now yielded a value closer to 129–130 GeV/c². Despite the fact that the original prediction wound up being borne out by experiment, the reasoning behind it no longer holds up.

This puts us in a particularly precarious position. We have a formula — simple in structure — that appears to work anywhere from “marginally well” to “extremely well” in providing a relationship between a certain fundamental property of matter, rest mass, that cannot be predicted by any theoretical means known today. In many ways, we’ve reached the limit of the Standard Model of particle physics, as every meaningful prediction that can be extracted from the theory concerning observable quantities has already been teased out.

And yet, the mysterious nature of mass exhibits these approximate relationships. Is there some fundamental reason why the fermions in our Universe come in exactly three copies? Is there a reason why the bosons don’t? Is there a reason why the heavy quarks and the charged leptons give the same constant of 2/3 for the Koide formula, but the light quarks are closer to 5/9 and the massive bosons are closer to (but inconsistent with exactly) a value of 1/3? And just what, precisely, are the fundamental masses of the neutrinos, and what sort of hierarchy do they display?

By taking the sum of any three numbers, while simultaneously dividing them by the square of the sum of each of their square roots, you’ll always get a number between 1/3 and 1, without exception. When all three numbers are equal, you get 1/3; if one number is much, much greater than the other two, you get 1. In the Standard Model, we have precisely three generations of fermions. So why is it, then, for both the charged leptons and the three heaviest quarks, that we get a value precisely between those two: of 2/3, while the light quarks give 5/9 and the massive bosons give us a value just a tiny bit larger than 1/3?

At this point, we have no idea. It could all be a simple numerical coincidence, with no rhyme or reason beyond the fact that these “values” only approximately match the implied correlation. Or, just maybe, it’s a 40-year-old hint of what might underpin or even take us beyond the Standard Model: a possible mass relation between fundamental particles that the Standard Model itself offers no explanation for. One of the greatest mysteries in physics is why particles have the properties they do. If the Koide formula turns out to be somehow connected to the property of rest mass, we just might have seen an impeccable hint to guide us down the unknown road that lies before us.

Starts With A Bang is written by Ethan Siegel, Ph.D., author of Beyond The Galaxy, and Treknology: The Science of Star Trek from Tricorders to Warp Drive.