How Is The Universe Accelerating If The Expansion Rate Is Dropping?

Travel the universe with Dr. Ethan Siegel as he answers the biggest questions of all

The expansion rate is dropping, but distant galaxies are accelerating. Here’s how.

If you take a look at any galaxy in the Universe that isn’t gravitationally bound to our own, we’ve already learned what’s going to happen to it in the future. Our Local Group, consisting of our Milky Way, Andromeda, and about 60 smaller galaxies, are the only ones bound to us. If you considered any other galaxy as part of the bound structure it’s a member of — like a galaxy pair, group, or cluster — that entire structure is receding from us, with its light systematically shifted towards longer wavelengths: a cosmic redshift. The farther away a galaxy is, on average, the greater the amount of its redshift, implying that the Universe is expanding.

Moreover, if you were to hang around for large amounts of cosmic time, you’d find that this galaxy is speeding up in its recession from us. As time goes on, it will redshift by greater and greater amounts, implying that the Universe is not only expanding, but that it’s accelerating. The inferred speed for any galaxy (that isn’t gravitationally bound to us) will rise over time, and all such galaxies will eventually become unreachable, even at the speed of light. And yet, if we were to measure the expansion rate of the Universe, what we commonly call the Hubble constant, we’d find that it’s actually dropping over time, not rising.

Here’s how, in an accelerating Universe, that’s actually possible.

Instead of an empty, blank, three-dimensional grid, putting a mass down causes what would have been ‘straight’ lines to instead become curved by a specific amount. The curvature of space due to the gravitational effects of Earth is one visualization of gravitation, and is a fundamental way that General Relativity differs from Special Relativity. (CHRISTOPHER VITALE OF NETWORKOLOGIES AND THE PRATT INSTITUTE)

The first thing you have to realize is that in our theory of gravity — Einstein’s General Relativity — there’s a tremendously powerful relationship between the matter and energy in our Universe and the way that space and time behave. The presence, amount, and types of matter and energy present determine how space and time curve and evolve over time, and that curved spacetime tells matter and energy how to move.

Einstein’s theory is tremendously complicated; it took months for the first exact solution to be found in General Relativity, and that was for a Universe with one non-rotating, uncharged point mass in it. More than 100 years later, there are still only perhaps two dozen exact solutions are known.

Fortunately, one of them is for a Universe that’s uniformly filled in all locations with roughly equal amounts of matter, radiation, and any other forms of energy you can dream up. When we look out at the Universe and measure it, on the largest cosmic scales, this appears to describe what we see.

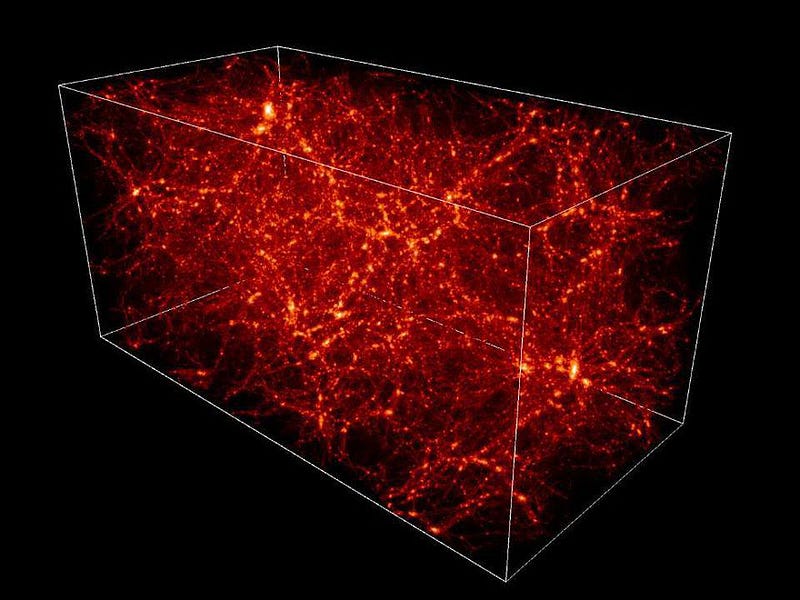
In modern cosmology, a large-scale web of dark matter and normal matter permeates the Universe. On the scales of individual galaxies and smaller, the structures formed by matter are highly non-linear, with densities that depart from the average density by enormous amounts. On very large scales, however, the density of any region of space is very close to the average density: to about 99.99% accuracy. (WESTERN WASHINGTON UNIVERSITY)

A Universe filled with the same amount of stuff everywhere, from the earliest times (which we see imprinted in the Cosmic Microwave Background) to the present day (where we can count galaxies and quasars), seems to be exactly what we have. And if that’s the Universe in which you live, there’s a specific solution that describes the spacetime you occupy: the Friedmann-Lemaître-Robertson-Walker spacetime.

What this spacetime tells us is remarkable. On one side of the equation, you get all the different forms of energy that can be present:

normal matter,
antimatter,
dark matter,
neutrinos,
radiation (like photons),
dark energy,
spatial curvature,
and anything else we can dream up.

And on the other side? An expression that we quickly realized was how the fabric of space changed over time: either growing or shrinking. We could only tell which one was true by observing it.

A photo of the author at the American Astronomical Society’s hyperwall, along with the first Friedmann equation (in modern form) at right. Dark energy could either be treated as a form of energy with a constant energy density or as a cosmological constant, but exists on the right-hand side of the equation. (PERIMETER INSTITUTE / HARLEY THRONSON / E. SIEGEL)

This one equation, called by some the most important equation in the Universe, tells us how the Universe evolves over time. Think about what it means: the rate at which the Universe either expands or contracts is directly related to the sum total of all the matter and energy — in all its different forms — present within it.

Before we had ever measured it, the widespread assumption was that the Universe was neither expanding nor contracting, but static. When Einstein realized that his equations predicted that a Universe full of stuff would be unstable against gravitational collapse, he threw in a cosmological constant to exactly balance out the force of gravity; the only way he could think of to prevent the Universe from imploding in a Big Crunch.

Even when it was pointed out to him directly by some (including Lemaître), Einstein derided the possibility that the Universe could be anything other than static. “Your calculations are correct, but your physics is abominable,” Einstein wrote in response to Lemaître’s work. And yet, when the key observations of Hubble came in, the results were unmistakable: the Universe was indeed expanding, and completely inconsistent with a static solution.

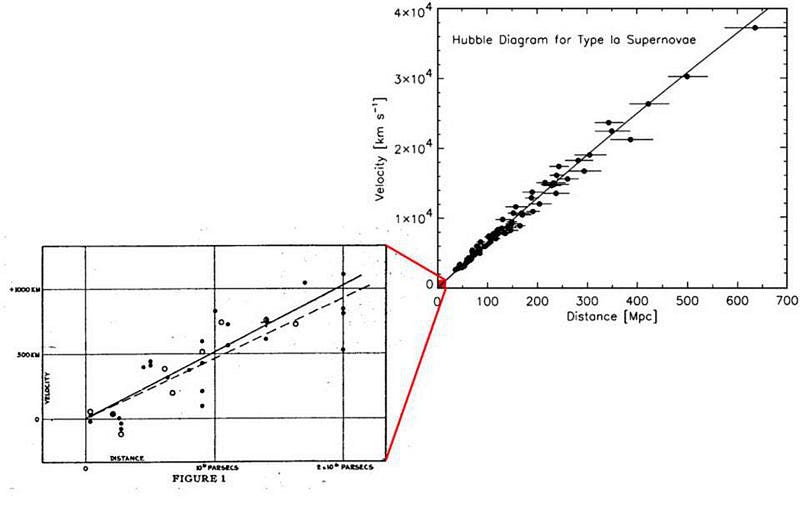
The original 1929 observations of the Hubble expansion of the Universe, followed by subsequently more detailed, but also uncertain, observations. Hubble’s graph clearly shows the redshift-distance relation with superior data to his predecessors and competitors; the modern equivalents go much farther. All the data points towards an expanding Universe. (ROBERT P. KIRSHNER (R), EDWIN HUBBLE (L))

An expanding Universe is one that was smaller in the past, and grows to occupy larger and larger volumes in the future. It’s one that was hotter in the past, since radiation is defined by the size of its wavelength, and as the Universe expands, this expansion stretches the wavelengths of any photons as they travel through intergalactic space, with the amount of stretching related to the amount of cooling. And it’s one that was even more uniform in the past, as an almost-uniform Universe that gravitates will see those tiny initial overdensities grow into the large-scale structure we observe today.

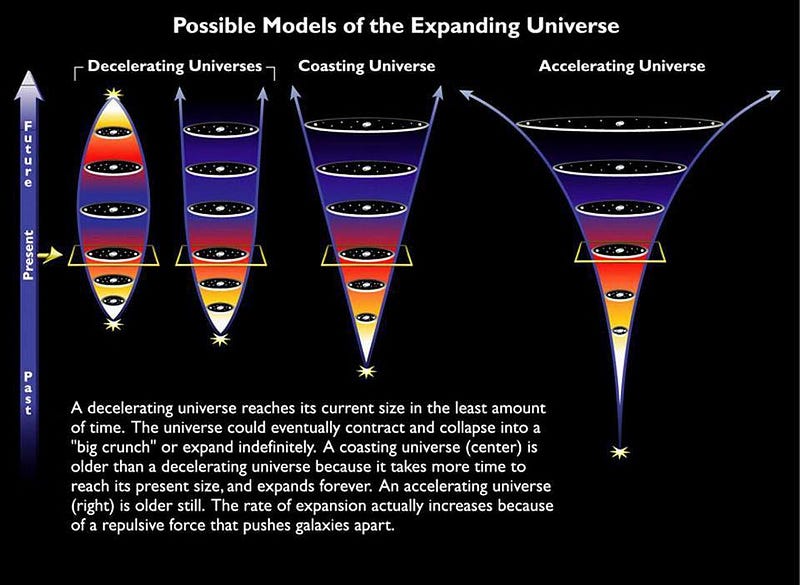
The big question, of course, is how the Universe’s expansion rate changes over time, and that’s dependent on the different forms of energy that are present within it. The volume of the Universe will continue to grow regardless of what’s in it, but the rate at which the Universe grows will change dependent on exactly what types of energy it’s filled with.

Let’s look at some examples in detail.

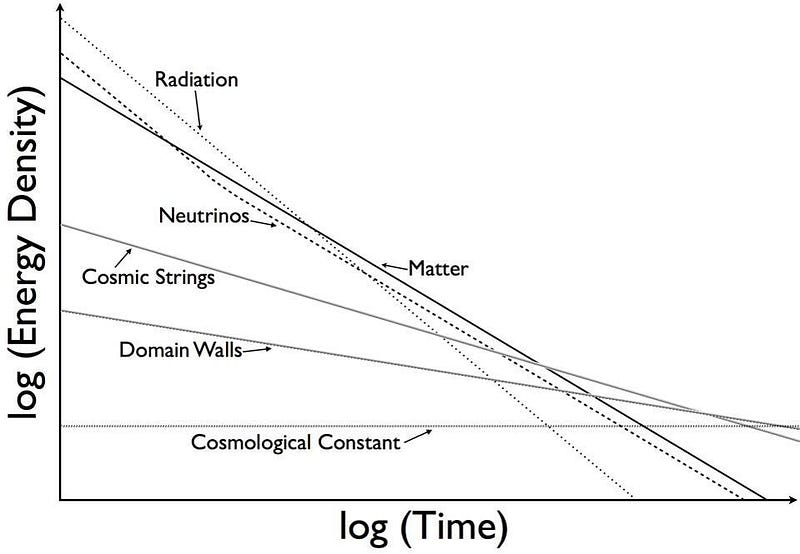
Various components of and contributors to the Universe’s energy density, and when they might dominate. Note that radiation is dominant over matter for roughly the first 9,000 years, then matter dominates, and finally, a cosmological constant emerges. (The others do not exist in appreciable amounts.) However, dark energy may not be a pure cosmological constant. (E. SIEGEL / BEYOND THE GALAXY)

If we had a Universe that was 100% made of matter, with nothing else at all, it would expand at a rate that grew as ~t^⅔, where if you doubled the age of the Universe, your size (in each of the three dimensions) would grow by 58%, while your volume would roughly quadruple.

If we had a Universe that was 100% made of radiation, again with nothing else at all, it would expand at a rate that grew as ~t^½. If you doubled the age of your Universe, your size would increase by 41% in each dimension, while the volume increases to about 2.8 times its original value.

And if you had a Universe that was filled with dark energy — and if we assume that dark energy turns out to truly be a cosmological constant — the Universe wouldn’t expand as a power law in time, but as an exponential. It would grow as ~e^Ht, where H is the expansion rate at any particular moment in time.

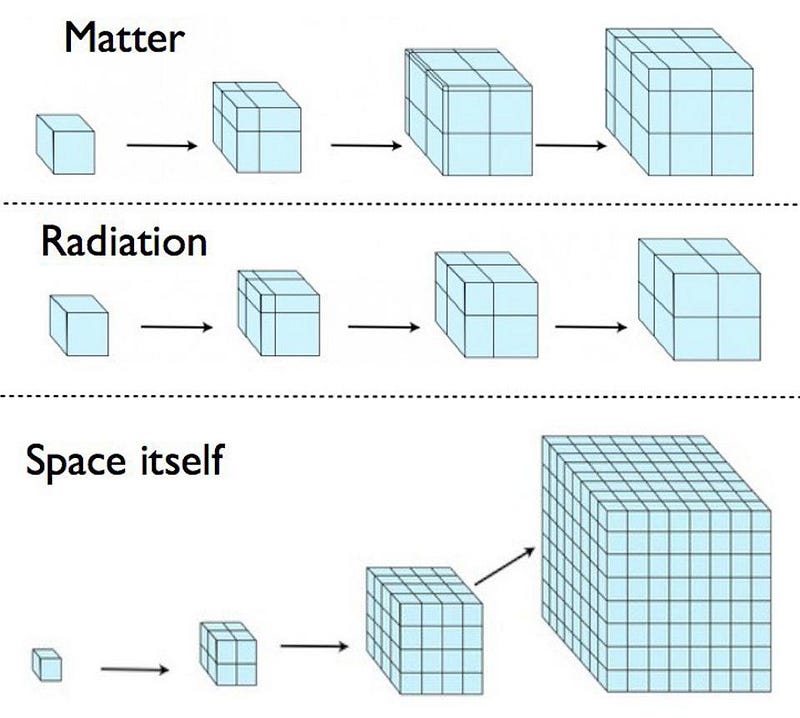
An illustration of how spacetime expands when it’s dominated by Matter, Radiation or energy inherent to space itself: dark energy. All three of these solutions are derivable from the Friedmann equations, and these solutions can be combined to represent a Universe with all three components, much like our own. (E. SIEGEL)

Why are these three cases so different from one another? The best way to think about it is to allow them to all start off like they’re the same Universe. They have the same initial expansion rate, the same initial volume, and the same amount of total energy present within that volume.

But as they start to expand, what happens?

The matter-filled Universe dilutes; its density drops as the volume expands, all while the mass (and hence the energy, since E = mc²) remains constant. As the energy density drops, so does the expansion rate.
The radiation-filled Universe dilutes faster; it’s density drops as the volume expands, while each individual photon also loses energy due to its cosmological redshift. The energy density drops faster for a radiation-filled Universe than a matter-filled one, and therefore so does the expansion rate.
But a Universe filled with dark energy — a cosmological constant — doesn’t dilute. The energy density remains constant: the definition of a cosmological constant. As the volume of the Universe expands, the total amount of energy goes up, keeping the expansion rate constant.

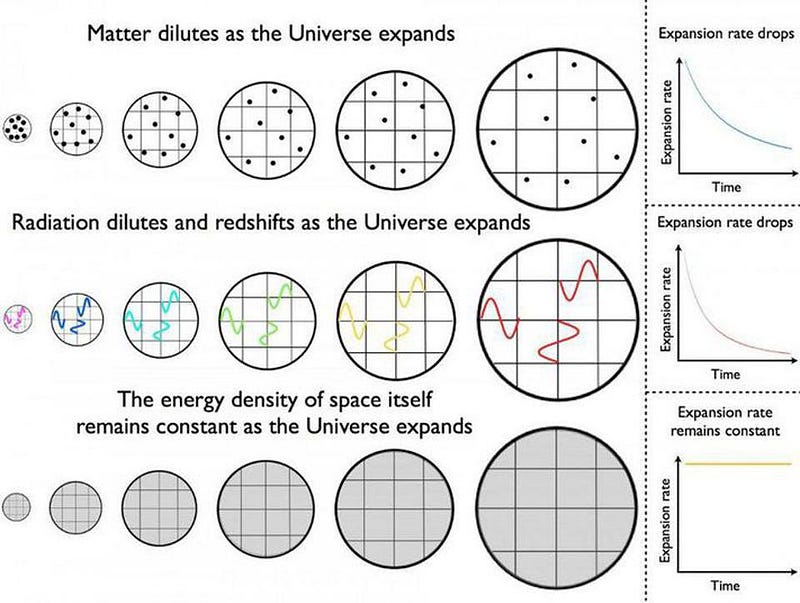
While matter (both normal and dark) and radiation become less dense as the Universe expands owing to its increasing volume, dark energy, and also the field energy during inflation, is a form of energy inherent to space itself. As new space gets created in the expanding Universe, the dark energy density remains constant. (E. SIEGEL / BEYOND THE GALAXY)

If you were to then imagine that, in each of these Universes, you were located at the same point, and there were one other galaxy in the Universe (corresponding to a different point), you could watch it recede away from you over time. You could measure how its distance was changing with time, and you could measure how its redshift (which corresponds to its recession speed) changed with time.

In the matter-filled Universe, the other galaxy would get farther and farther away from you as time went on, but it moves away from you more slowly in the process. Gravity works to counteract the expansion, failing to stop it but succeeding in slowing it down. In a matter-only Universe, the expansion rate continues to drop, eventually approaching zero.
In the radiation-filled Universe, the other galaxy still gets farther and farther away as time goes on, but the galaxy not only moves away more slowly as time goes on, it slows down faster than in the matter-only case. The expansion rate still asymptotes to zero, but the distant galaxy remains closer and moves away more slowly than in the matter-filled version.
But in the dark energy-filled Universe, the other galaxy gets farther away and does so at an increasingly faster speed. When it’s double the initial distance away, it now appears to be receding at double the speed. At 10 times the distance, it’s 10 times the speed. Even though the expansion rate is a constant, any individual galaxy speeds up as it recedes from us over time.

(If you’re curious, there’s an on-the-border case: an empty Universe, where only curvature determines the expansion. In this Universe, the other galaxy gets farther away, but its recession speed would remain constant.)

A plot of the apparent expansion rate (y-axis) vs. distance (x-axis) is consistent with a Universe that expanded faster in the past, but is still expanding today. This is a modern version of, extending thousands of times farther than, Hubble’s original work. The various curves represent Universes made out of different constituent components. (NED WRIGHT, BASED ON THE LATEST DATA FROM BETOULE ET AL. (2014))

This might not make intuitive sense to you, so let’s bring a little bit of math in to help. The expansion rate, today, is ~70 km/s/Mpc. Take a look at those weird units! The expansion rate is a speed (70 km/s) that accumulates with cosmic distance (for each Mpc, or megaparsec, which corresponds to ~3.26 million light-years). If something’s 10 Mpc away, it recedes at ~700 km/s; if it’s 1,000 Mpc away, it recedes at 70,000 km/s.

In a matter-filled or radiation-filled Universe, the expansion rate itself drops with time, so even as a galaxy gets more distant, the expansion rate slows down by a greater percentage than its distance goes up. But in a dark energy-filled Universe, the expansion rate is constant, so as a galaxy gets more distant, it moves away faster and faster.

The largest contributors to our Universe’s energy today are matter (at ~32%) and dark energy (at ~68%). The matter part continues to dilute, while the dark energy part remains constant. Since both contribute, the expansion rate continues to drop, and will eventually asymptote to a value of ~45–50 km/s/Mpc. However, a distant galaxy still speeds up as it moves away from us, something that’s been going on for the past 6 billion years in our 13.8 billion year history. The expansion rate is dropping, but the speeds of distant galaxies are still increasing, or accelerating.

The different possible fates of the Universe, with our actual, accelerating fate shown at the right. After enough time goes by, the acceleration will leave every bound galactic or supergalactic structure completely isolated in the Universe, as all the other structures accelerate irrevocably away. We can only look to the past to infer dark energy’s presence and properties, which require at least one constant, but its implications are larger for the future. (NASA & ESA)

That’s the big key to understanding this: as the Universe expands, we can measure two different things. We can measure the expansion rate, which tells us, for every megaparsec a galaxy is away from us, how fast it recedes. This expansion rate, a speed-per-unit-distance, changes over time, dependent on the amount of energy present within a given volume of the Universe. As the Universe expands, the amount of dark energy in a given volume stays the same, but the matter and energy densities go down, and therefore so does the expansion rate.

But you can also measure a distant galaxy’s recession speed, and in a Universe dominated by dark energy, that speed will increase over time: an acceleration. The expansion rate drops, asymptoting to a constant (but positive) value, while the expansion speed increases, accelerating into the oblivion of expanding space. Both of these things are simultaneously true: the Universe is accelerating and the expansion rate is very slowly dropping. At last, now you finally understand how it happens, too.

Starts With A Bang is written by Ethan Siegel, Ph.D., author of Beyond The Galaxy, and Treknology: The Science of Star Trek from Tricorders to Warp Drive.

Travel the universe with Dr. Ethan Siegel as he answers the biggest questions of all