Ask Ethan: Where Is The Line Between Mathematics And Physics?

They seem almost indistinguishable in some regards, but only one of them represents our physical Universe.

When it comes to describing the physical world, we can do it anecdotally, as we commonly do, or we can use science. That means gathering quantitative data, finding correlations between observables, formulating physical laws and theories, and writing down equations that allow us to predict the outcomes of various situations. The more advanced the physical situation we’re describing, the more abstract and complex the equations and the theoretical framework gets. But in the act of formulating those theories, and writing the equations that describe what will happen under a variety of conditions, aren’t we leaping into the realm of mathematics, rather than physics? Where is that line? That’s the question of our Patreon supporter Rob Hansen, who asks:

Where does one draw the line between abstract mathematics and physics? Is Noether’s Theorem part of the scientific corpus of knowledge, or the mathematical? What about Maldacena’s conjecture?

Luckily, we don’t have to go to such complicated examples to find the difference.

Imagine that you do something as simple as throwing a ball. At any instant in time, if you tell me where it is (its position) and how it’s moving (its velocity), I can predict for you exactly where and when it will hit the ground. Except, if you simply write down and solve the equations governed by Newton’s laws of motion, you won’t get a single, correct answer. Instead, you’ll get two answers: one that corresponds to the ball hitting the ground in the future, and one that corresponds to where the ball would have hit the ground in the past. The mathematics of the equations doesn’t tell you which answer, the positive or the negative one, is physically correct. It’s like asking what the square root of four is: your instinct is to say “two,” but it could just as easily be negative two. Math, on its own, isn’t always deterministic.

In fact, there’s no universal rule at all that you can apply to tell you which answer is the one you’re looking for! That, right there, is the biggest distinction between math and physics: math tells you what the possible solutions are, but physics is what allows you to choose the solution that describes our Universe.

This is, of course, a very simplistic example, and one where we can apply a straightforward rule: pick the solution that’s forward in time and ahead in space. But that rule won’t apply in the context of every theory, like relativity and quantum mechanics. When the equations are less physically intuitive, it’s much more difficult to know which possible solution is the physically meaningful one.

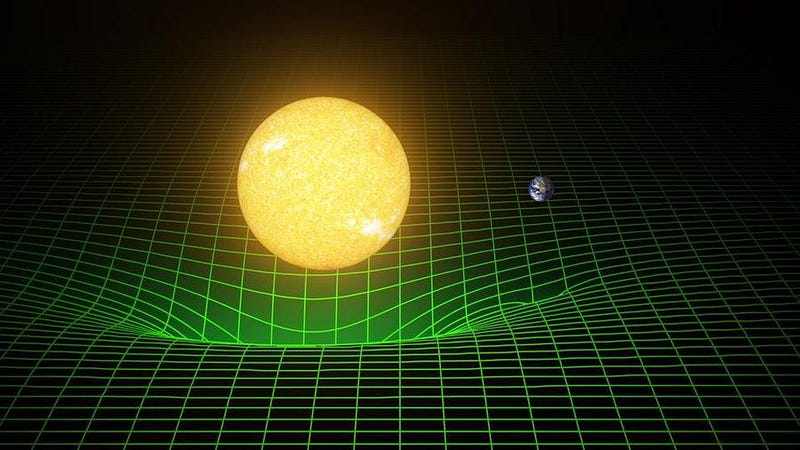
What, then, are you supposed to do when the mathematics gets more abstract? What do you do when you get to General Relativity, or Quantum Field Theory, or even more far afield into the speculative realms of cosmic inflation, extra dimensions, grand unified theories, or string theory? The mathematical structures that you build to describe these possibilities simply are what they are; on their own, they won’t offer you any physical insights. But if you can pull out either observable quantities, or connections to physically observable quantities, that’s when you start crossing over into something that you can test and observe.

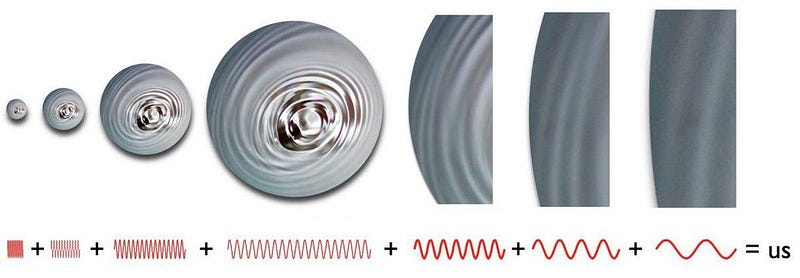
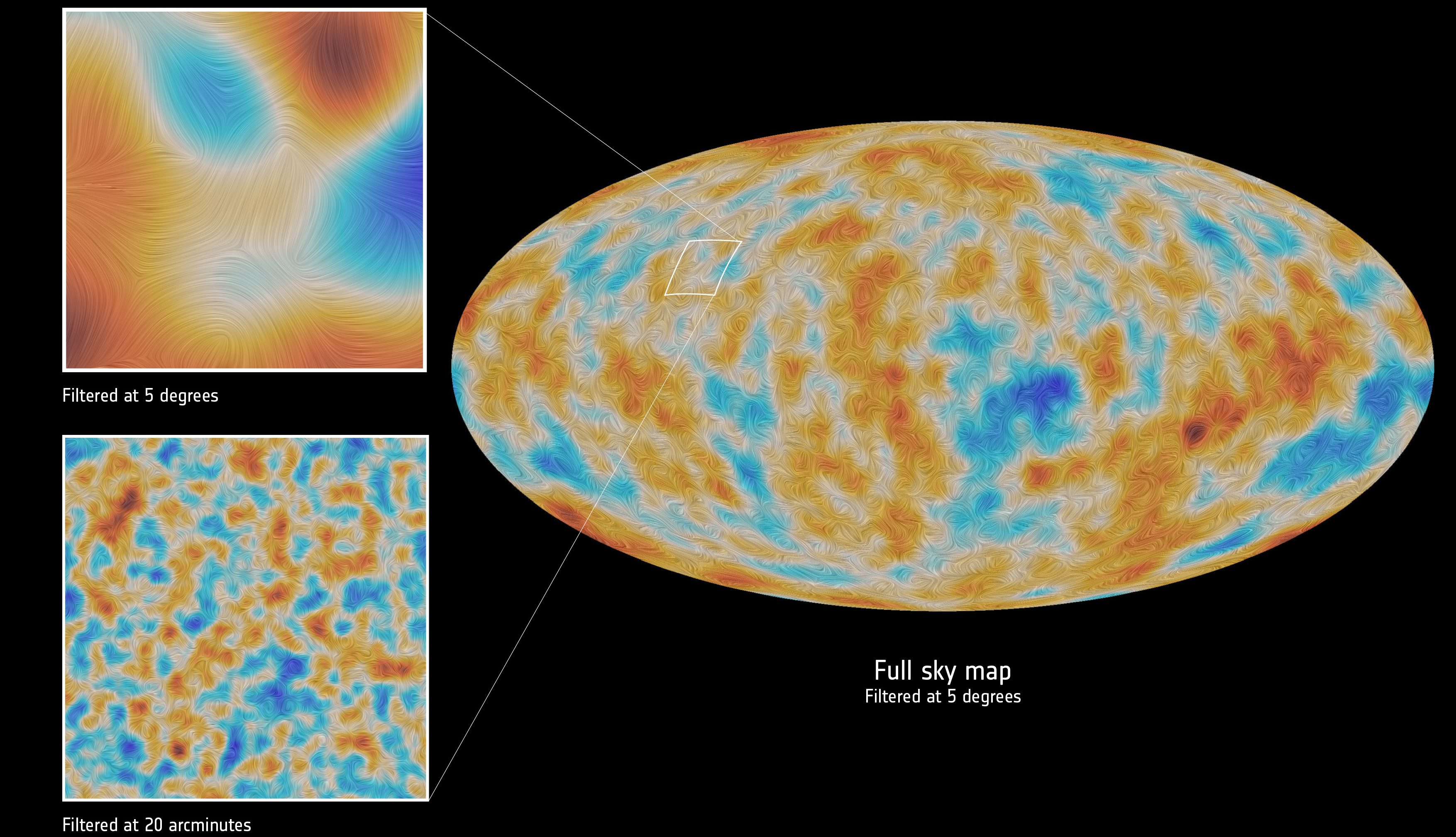
In inflationary cosmology, for example, there are all sorts of complicated equations that govern what’s going on. It sounds a lot like mathematics, and in many of the discussions, it sounds very little like physics. But the key is to connect what these mathematical equations predict with physical observables. For example, based on the fact that you have quantum fluctuations in the fabric of space itself, but space is stretching and expanding at an exponential rate during inflation, you’ll expect there to be ripples and imperfections in the value of the quantum field causing inflation all across the Universe. When inflation ends, those fluctuations become density fluctuations, which we can then go and look for as temperature fluctuations in the Big Bang’s leftover glow. This prediction of the 1980s was verified by satellites like COBE, WMAP, and Planck many years later.

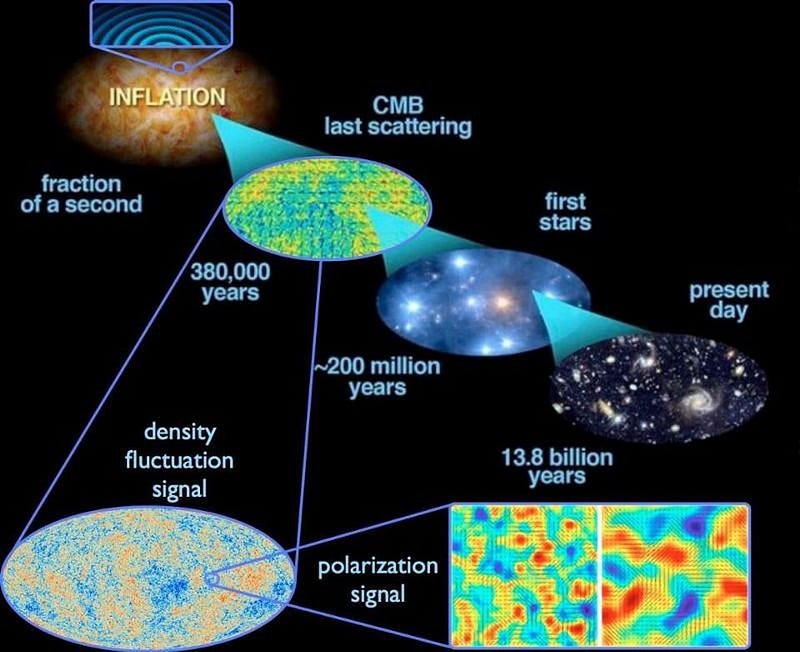
Noether’s theorem is an interesting example of a mathematical theorem that is powerful all on its own in mathematics, but has a very special application to physics. In general, the theorem tells you that if you have a system that takes the integral of a Lagrangian, and that system has a symmetry to it, there must be a conserved quantity associated with that symmetry. In physics, the integral of a Lagrangian function corresponds to what we physically call the “action,” and so any system that can be modeled with a Lagrangian alone, if it contains that symmetry, you can derive a conservation law from it. In physics, this allows us to derive things like the conservation of energy, the conservation of momentum, and the conservation of electric charge, among others.

What’s interesting about this is that if we couldn’t describe the Universe with these mathematical equations that contained these symmetries, there would be no reason to expect that these quantities would be conserved. This puzzles a lot of people, then, when they learn that in General Relativity, there is no universal time-translation symmetry, which means there isn’t a conservation of energy law for the expanding Universe we inhabit! Individual interaction in quantum field theory do obey that symmetry, so they do conserve energy. But on the scale of the entire Universe? Energy isn’t even defined, meaning we don’t know whether it’s conserved or not.

The Maldacena conjecture gets even more complicated. Also known as the AdS/CFT correspondence, it shows that there’s a mathematical duality — meaning the same equations govern both systems — between a Conformal Field Theory (like a force in quantum mechanics) and a string theory in Anti-de Sitter space, with one extra dimension. If two systems are governed by the same equations, that means their physics must be the same. So, in principle, we should be able to describe aspects of our four-dimensional (three space and one time) Universe equally as well by going to five-dimensional Anti-de Sitter spacetime, and choosing the right parameters. It’s the closest example we’ve ever found to an application of the holographic principle as it applies to our Universe.

Now, string theory (or, more accurately, string theories) have their own constraints governing them, as do the forces in our Universe, so it isn’t provably clear that there’s a one-to-one correspondence between our four-dimensional Universe with gravity, electromagnetism, and the nuclear forces and any version of string theory. It’s an interesting conjecture, and it has found some applications to the real world: in the study of quark-gluon plasmas. In that sense, it’s more than mathematics: it’s physics. But where it strays from physics into pure mathematics is not yet fully determined.

What all of this seems to be getting at is a more general question: why, and when, can we use mathematics to learn something about our physical Universe? We don’t know the answer to why, but we do know the answer to when: when it agrees with our experiments and observations. So long as the laws of physics remain the laws of physics, and do not whimsically turn on-and-off or vary in some ill-defined way, we know we can describe them mathematically, at least in principle. Mathematics, then, is the toolkit we use to describe the functioning of the Universe. It’s the raw materials: the nails, the boards, the hammers and saws. Physics is how you apply that mathematics. Physics is how you put it all together to make sense of your materials, and wind up with a house, for example, instead of a collection of parts that could, in principle, be used to build something entirely different.

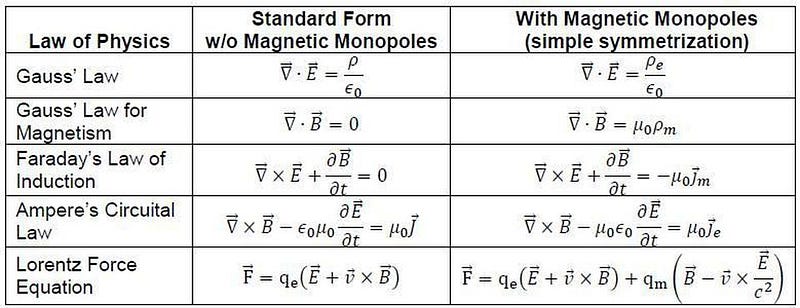
If you describe the Universe precisely, and you can make quantitative predictions about it, you’re physics. If those predictions turn out to be accurate and reflective of reality, then you’re physics that’s correct and useful. If those predictions are demonstrably wrong, you’re physics that doesn’t describe our Universe: you’re a failed attempt at a physical theory. But if your equations have no connection at all to the physical Universe, and cannot be related to anything you can ever hope to someday observe or measure, you’re firmly in the realm of mathematics; the divorce from physics will then be final. Mathematics is the language we use to describe physics, but not everything mathematical is physically meaningful. The connection, and where it breaks down, can only be determined by looking at the Universe itself.

Send in your Ask Ethan questions to startswithabang at gmail dot com!