Shocker: Nobel Prize in Physics goes to topology in materials, not gravitational waves!

If you were betting on LIGO, you bet wrong. Just like everybody else.

“‘Topology is destiny,’ he said, and put the drawers on. One leg at a time.” 
–Neal Stephenson

One week ago today, the 2016 Nobel Prize in Physics was announced: half to David J. Thouless, a quarter each to F. Duncan M. Haldane and J. Michael Kosterlitz, for theoretical discoveries of topological phase transitions and topological phases of matter. This was a huge upset, as everyone was anticipating the Nobel Prize would go various members of the LIGO collaboration, who earlier this year announced the first discovered gravitational waves from merging black holes. This year, the Nobel committee went with the more practical side, to the scientists who pioneered the ability to create controlled “holes” or defects in quantum mechanical states of matter known as condensates. Their research has led to breakthroughs in materials science and condensed matter physics, and holds the promise of revolutionizing electronics. It marks the 24th year in a row that the prize has been awarded to multiple individuals, and the 53rd consecutive year that women have been shut out of the prize.

There are two sides to making sense of the Universe: Einstein’s General Relativity, which governs the gravitational force and the evolution of spacetime, and quantum mechanics, which governs the other three fundamental forces and all the other interactions, phases and properties of matter. While the entire physics community has been abuzz with the first direct detection of gravitational waves, a longstanding prediction of Einstein’s theory confirmed earlier this year, there have been remarkable discoveries, breakthroughs and applications in what new states of matter can be created — and what they can accomplish for humanity — occurring continuously. While most of us think of three phases of matter, solid, liquid and gas, there’s a fourth state that occurs if you heat up a gas too severely: a plasma. But conversely, for some types of matter, there are phases that occur in nature when you cool a material too greatly: a condensate. Unlike all the other states of matter, condensates display unique properties not seen anywhere else in nature.

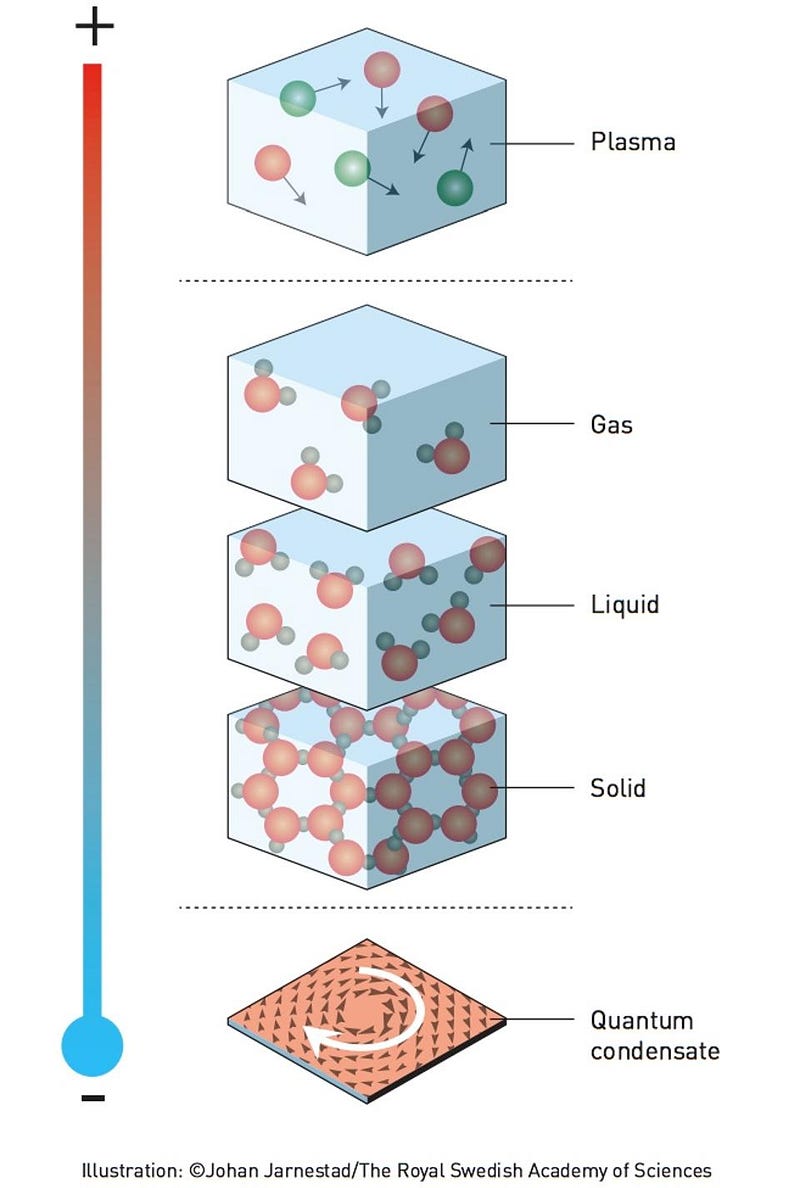
Quantum physics was an incredible revolution in how we look at the world, teaching us that:

• Nature is discrete, not continuous, made up of individual, fundamental particles known as quanta.
• That these quanta have a few different types of properties inherent to them that can never be altered: spin, electric charge, color charge, flavor, etc.
• And that when you make composite particles or systems out of them, there are new quantum properties that emerge as well: things like orbital angular momentum, isospin and non-zero physical sizes, for example.

But one of the most interesting things is that the properties of these particles and their interactions can appear incredibly different if you restrict what they can do to two dimensions — a flat surface — rather than through the usual three.

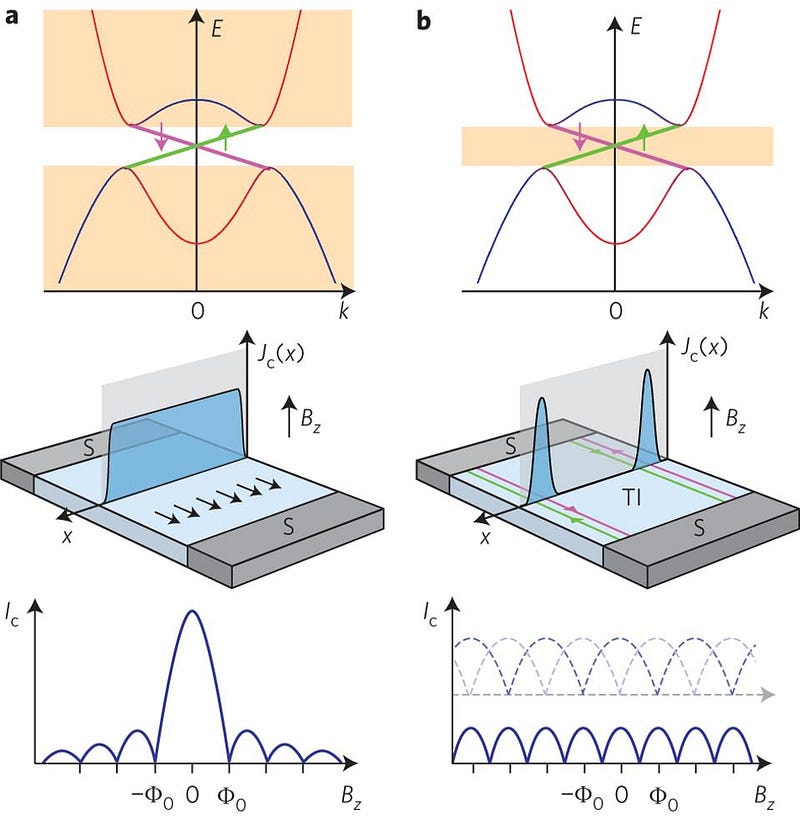
It was thought for a long time that superconductivity and superfluidity, two low-temperature properties of certain types of matter with either zero resistance or zero viscosity, respectively, required a fully three-dimensional material to work through. But in the 1970s, Michael Kosterlitz and David Thouless discovered that not only could they occur in thin, 2D layers, but they discovered the phase transition mechanism by which superconductivity would disappear at high enough temperatures. With fewer degrees of freedom, and fewer dimensions for particles, forces and interactions to travel through, quantum mechanical systems actually become easier to study. Equations that are difficult to solve in three dimensions often become much easier in only two; other equations that are impossible to solve in three dimensions actually have known solutions in two.

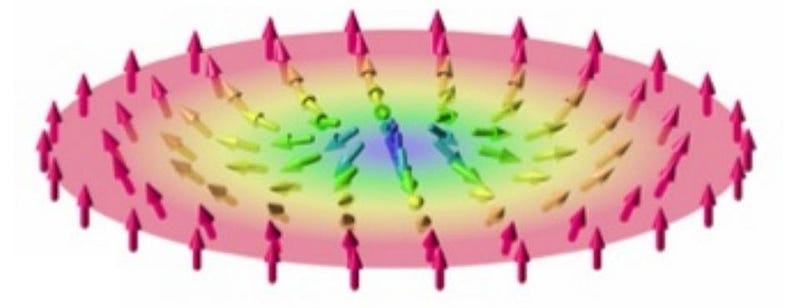
Many particles, quasiparticles and systems of particles are known to behave analogously to “topological defects,” which are like either “holes” (for a 0-dimensional defect) or “strings” (for a 1-dimensional defect) running through either 2D or 3D space. By applying the mathematics of topology to these low-temperature systems, new topological phases of matter could be predicted.

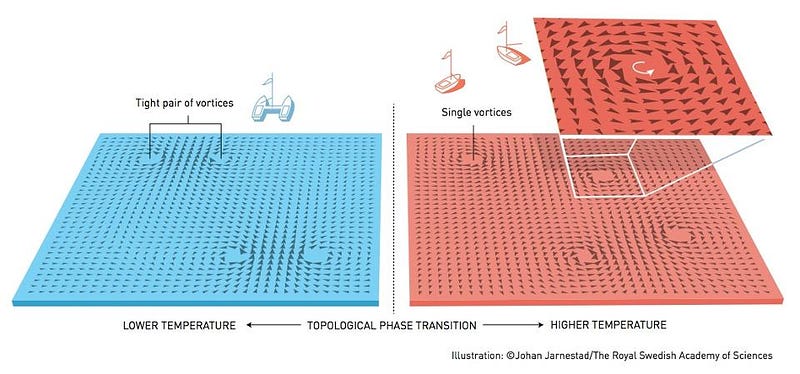
The nature of the transition from low temperature states (where vortex pairs form) to high temperature states (where the pairs become independent) obeys the Kosterlitz-Thouless phase transition rules. Combining quantum physics with topology leads to a number of physically interesting things happening in discrete, integer steps. The conductance of a thin, electrically conductive material occurs in these steps. Chains of small magnets behave topologically. The phase transition rules apply universally to all types of materials in two dimensions. In the 1980s, Kosterlitz himself discovered the conductance relation, while Duncan Haldane discovered the topological properties of small magnet chains. Although the applications now extend into other areas of physics — statistical mechanics, atomic physics, and hopefully soon into electronics and quantum computers — the physics underlying this discrete behavior of matter in lower dimensions is governed by the same topological rules as any mathematical system.

These new properties may only show themselves at very cold temperatures and in the presence of very high magnetic fields, but that doesn’t make them any less fundamental to nature than the properties we observe conventionally. The quantum hall effect, the fact that “integer” quantum magnets are topological while “half-integer” ones are not, and that you can determine the character of a quantum magnet simply by studying its edges were all advances brought forth by this year’s prizewinning trio. New and unexpected types of matter have been discovered by building on their research, including topological properties extending into fully 3D materials. Topological insulators, topological superconductors and topological metals are all being researched actively today, with the potential to revolutionize electronics and computation if-and-when they are successfully harnessed.

Alfred Nobel stated, when he developed the Nobel Prize, that it should go to the discovery responsible “for the greatest benefit to mankind.” The science here is not only proven, it’s well on its way to changing the way that we as humans live our daily lives. While there are certainly a very large number of deserving teams, individuals and discoveries, this year’s Nobel Prize reminds us all of the two main reasons we invest in fundamental science so heavily: for the knowledge and societal benefits we can reap for all of humanity. This year, a look back at what surprising things we’ve learned about matter under extreme conditions shows us how far our knowledge has come, while a look forward at what applications this might bring inspires us to pursue the next generation of quantum technologies. The indeterminate future is up to us.

This post first appeared at Forbes, and is brought to you ad-free by our Patreon supporters. Comment on our forum, & buy our first book: Beyond The Galaxy!