Ask Ethan: How small is an elementary particle?

What’s the difference between “point-like” and what we can actually state?

“When we think about the present, we veer wildly between the belief in chance and the evidence in favour of determinism. When we think about the past, however, it seems obvious that everything happened in the way that it was intended.” –Michel Houellebecq

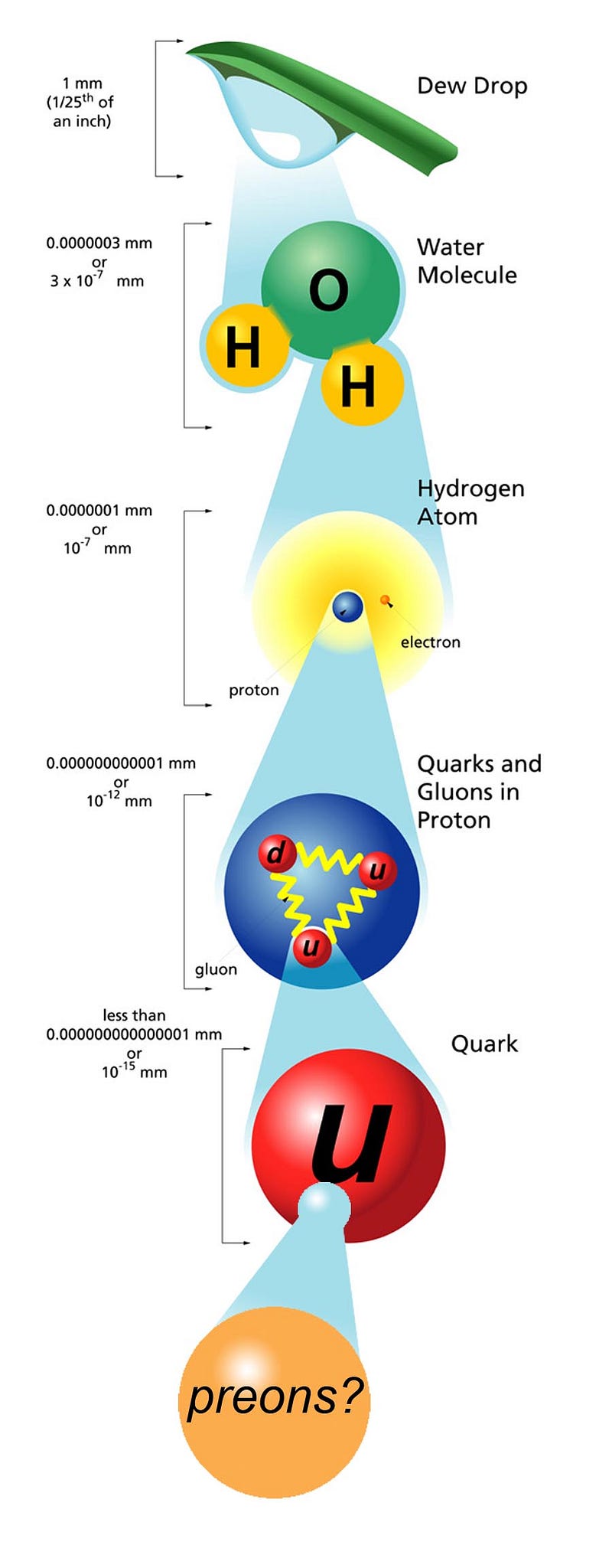
If you take any amount of matter, no matter how small or how large, there are only two options for what it’s made up of: either it can be split into something smaller, or it’s truly fundamental and indivisible. For most of the 19th century, we thought that atoms were that fundamental, smallest entity, since the greek words itself, ἄτομος, literally means “uncuttable.” But we know better now, and can split the atoms into nuclei and electrons, and the nuclei can be further split not only into protons and neutrons, but those entities themselves can be decomposed into more fundamental quarks and gluons. But can they be split further, and how do we know their “size” at all? Patrick Moore wants to know, as he asks:

What do scientists really mean when they state an elementary particle’s size?

“Size” is a difficult concept, but quantum mechanics is here to help.

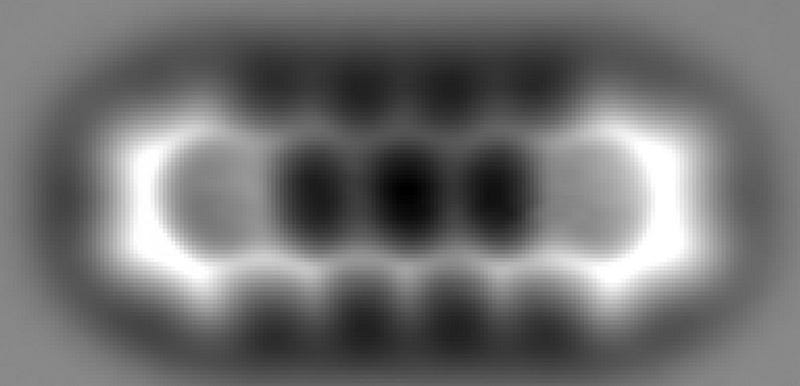
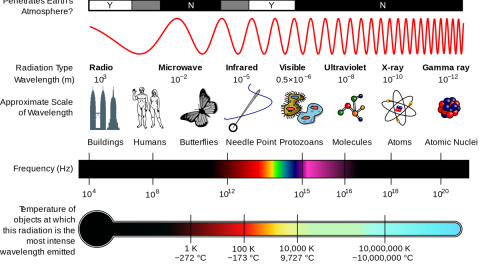
What you’re looking at, above, is a picture — taken with a technique not so different from a traditional photograph — of the individual atoms within a relatively simple molecule. It’s the fact that light is a wave that enables objects of a certain size to be imaged, but not anything that’s too small. You see, because light has a characteristic wavelength, it can interact with anything that’s roughly the size of that wavelength or larger, but not smaller. This is:

• why you need a relatively large antenna to pick up radio waves, since their long wavelengths require a substantial antenna to detect them,
• why the “holes” in the door of your microwave keep the microwaves in, because the wavelength of microwaves is larger than the size of the holes,
• and why tiny dust grains in space are good at blocking short-wavelength (blue) light, less good at blocking longer-wavelength (red) light, and why they’re totally transparent to even longer (infrared) radiation.

If you want to measure the size of the smallest particles, you need photons with smaller and smaller wavelengths. Because of the relationship between a photon’s energy and wavelength — they’re inversely proportional — that means you need to go to higher and higher energies to probe the smallest scales of all.

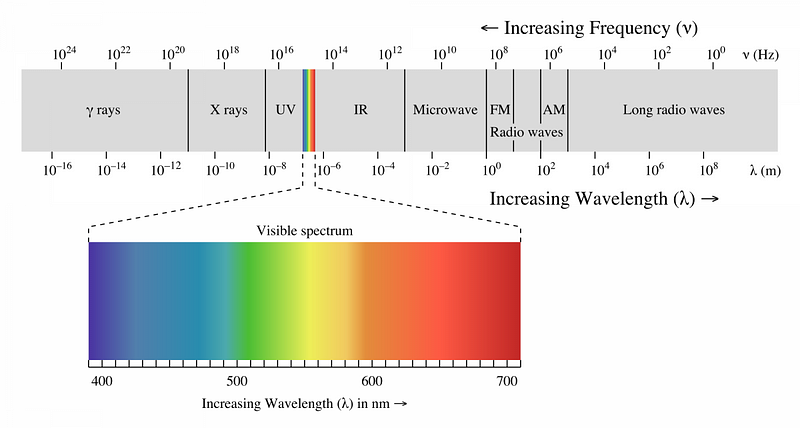
But photons aren’t the only way to go; it’s possible to use any particles at high energies to probe the size of matter. One of the funny rules of quantum mechanics in nature is that it isn’t just particles of light that act as waves, but any particles at all, including composite particles like protons and indivisible ones like (so far) the electron has proven to be. It’s by going to high energies and colliding with a stationary target that we can either determine the size of a non-fundamental “particle” by seeing when it splits apart, or determine that if a particle isn’t fundamental, it will only show that property “below” a certain size.

This was the very technique that enabled us to determine that:

• Atoms aren’t indivisible, but are made up of electrons and nuclei with a size of ~1 Å, or 10^–10 meters.
• Nuclei themselves can be further split into protons and neutrons, each with a size of ~1 fm, or 10^–15 meters.
• And if you bombard the particles inside protons and neutrons — the quarks and gluons — with high-energy particles, they don’t show any internal structure, just like electrons.

For each of the particles of the Standard Model, we’ve determined that if they have a composite nature, or a physical “size” that differs from point-like, it must be less than 10^–19 meters or so.

We might not think of this as weird, but there was a time where people didn’t know quantum mechanics, but they did know Einstein’s famous equation: E = mc2. If you said that an electron has the charge you measure it to have, and the electric potential energy was responsible for its mass, you could derive a size for it, known as the classical electron radius. This turns out to be pretty small, and equal to:

But we know this is wrong! This even turns out to be substantially larger than the size of a proton, and is larger by more than a factor of 1,000 from our best constraints. In other words, the particles we find are truly quantum in nature, and that means — if we go to arbitrarily high energies — the truly fundamental ones should be point-like.

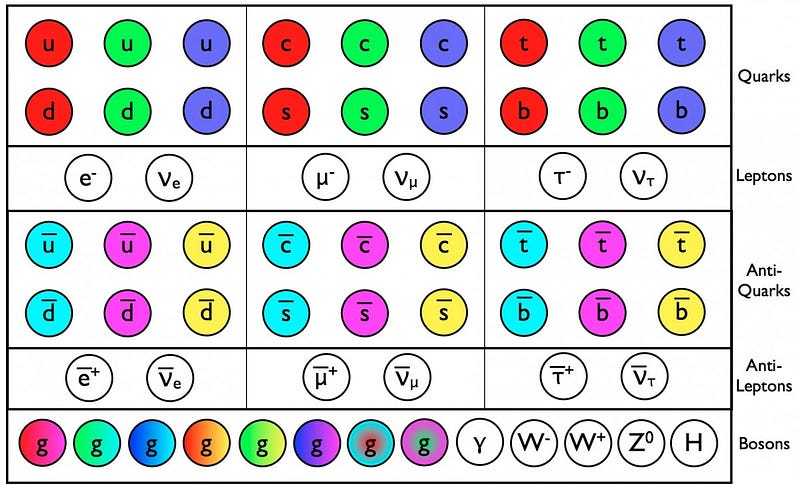
So when we talk about the size of an elementary particle, we talk about the search for something truly fundamental. Are the standard model particle truly indivisible? If so, we should be able to keep on going to high and higher energies, and should discover nothing that differs from point-like behavior all the way up to the Planck energy, or down to distance scales of 10–35 meters. Below that distance scale, physics doesn’t give sensible predictions, but we keep approaching it. Perhaps along the way, we’ll find that some (or all) of these particles can be further broken down, or perhaps that they’re made up of strings or membranes, or, alternatively, that they’re simply points all the way down. But all we know to date, as far as the actual sizes of particles, are the sizes of the non-fundamental ones. Everything else is just an upper limit, and the search to get to smaller and smaller scales continues.

Submit your Ask Ethan questions to startswithabang at gmail dot com!

This post first appeared at Forbes, and is brought to you ad-free by our Patreon supporters. Comment on our forum, & buy our first book: Beyond The Galaxy!