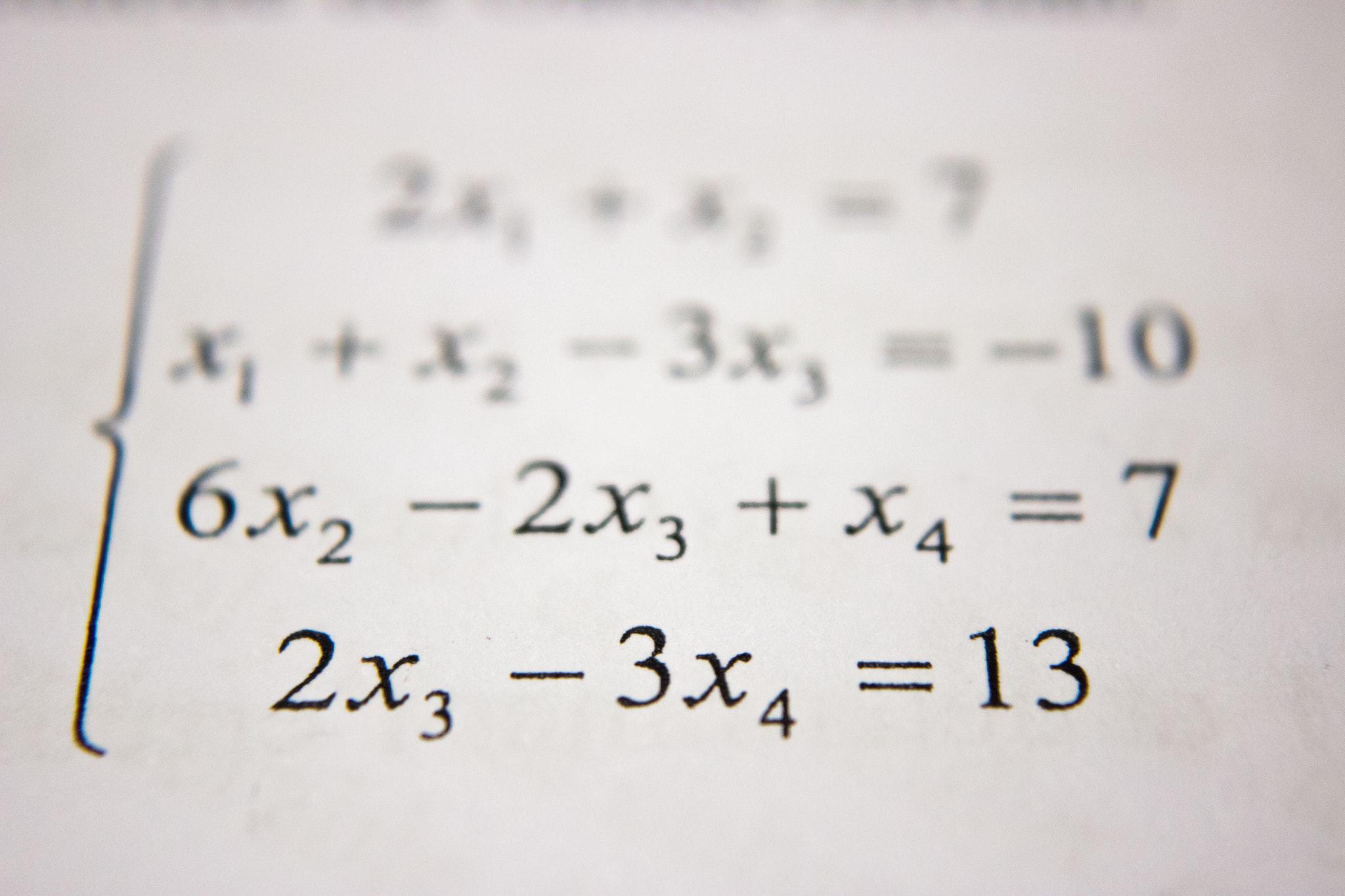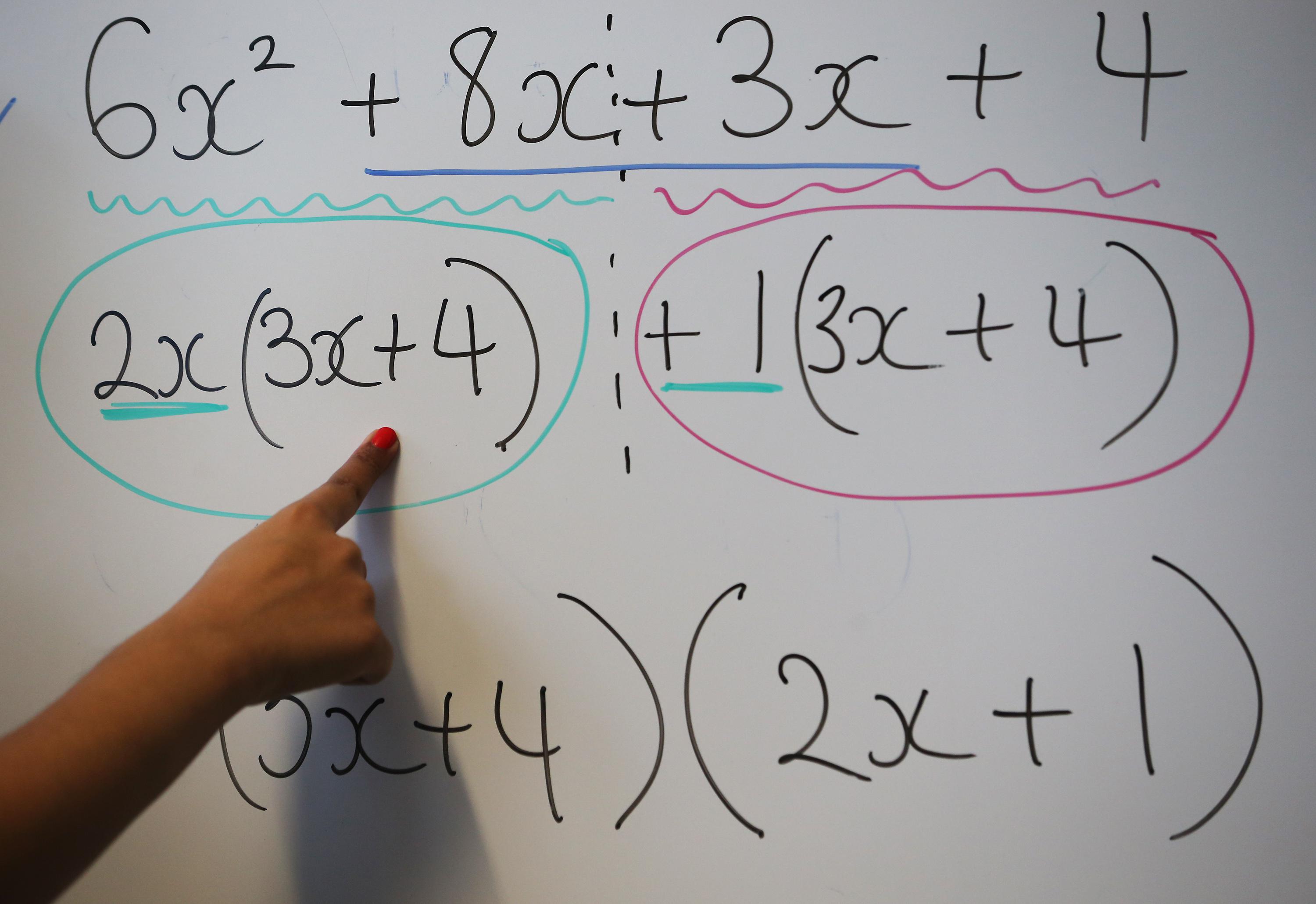mathematics

The strange, undulating sound of mathematics.

Math can explain why your laces spontaneously come untied — and how to stop it.

Is history decided by discernible laws or does it unfold based on random, unpredictable occurrences?

Could anyone still meet the Theoretical Minimum?

Symmetrical objects are less complex than non-symmetrical ones. Perhaps evolution acts as an algorithm with a bias toward simplicity.

Singularities frustrate our understanding. But behind every singularity in physics hides a secret door to a new understanding of the world.

The very concept of a “problem with no solution” goes against human nature. But we must accept this harsh reality to have peace in our lives.

Thales may have known the famous theorem perhaps as much as half a century before Pythagoras.

We spend much of our early years learning arithmetic and algebra. What’s the use?

The ancient Greeks were obsessed with geometry, which may have formed the basis of their philosophical cosmology.

If computers can beat us at chess, maybe they could beat us at math, too.

Pythagoras may have believed that the entire cosmos was constructed out of right triangles.

Philosopher and logician Kurt Gödel upended our understanding of mathematics and truth.

Is information the fifth form of matter?

The I Ching serves as a foundation for many Eastern philosophies and Western mathematics.

Research shows that the way math is taught in schools and how its conceptualized as a subject is severely impairing American student’s ability to learn and understand the material.

One prominent mathematician asks: was Einstein such a smartypants after all?

Mathematicians are working to combat partisan gerrymandering.

So you think you’re “not a math person”? International Mathematical Olympiad coach Po-Shen Loh strongly disagrees.

Mathematics professor Po-Shen Loh has created Expii, a free education tool that democratizes learning by turning your smartphone into a tutor.

Few see how strongly science’s preferred languages shape and limit the thinking of many experts.