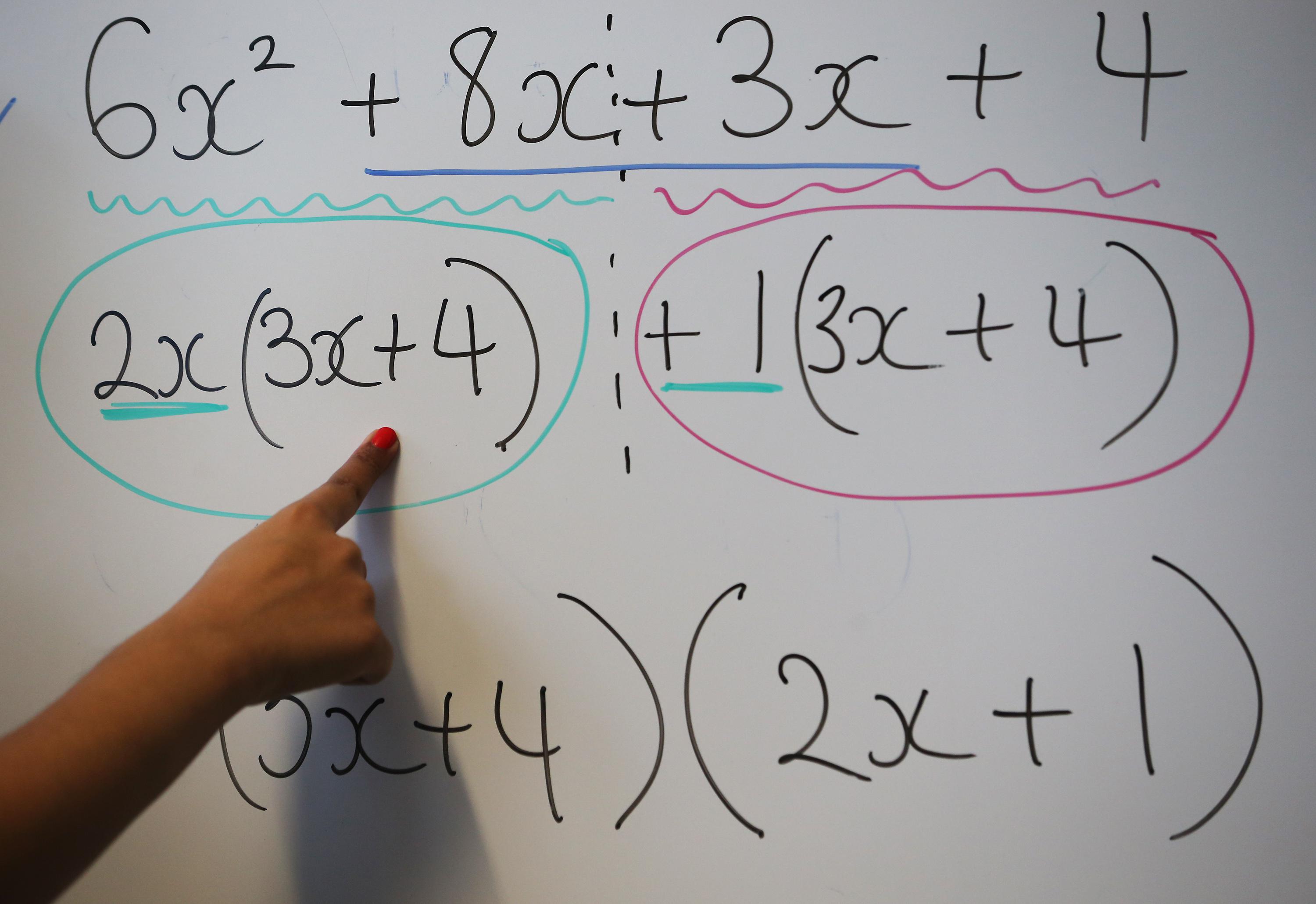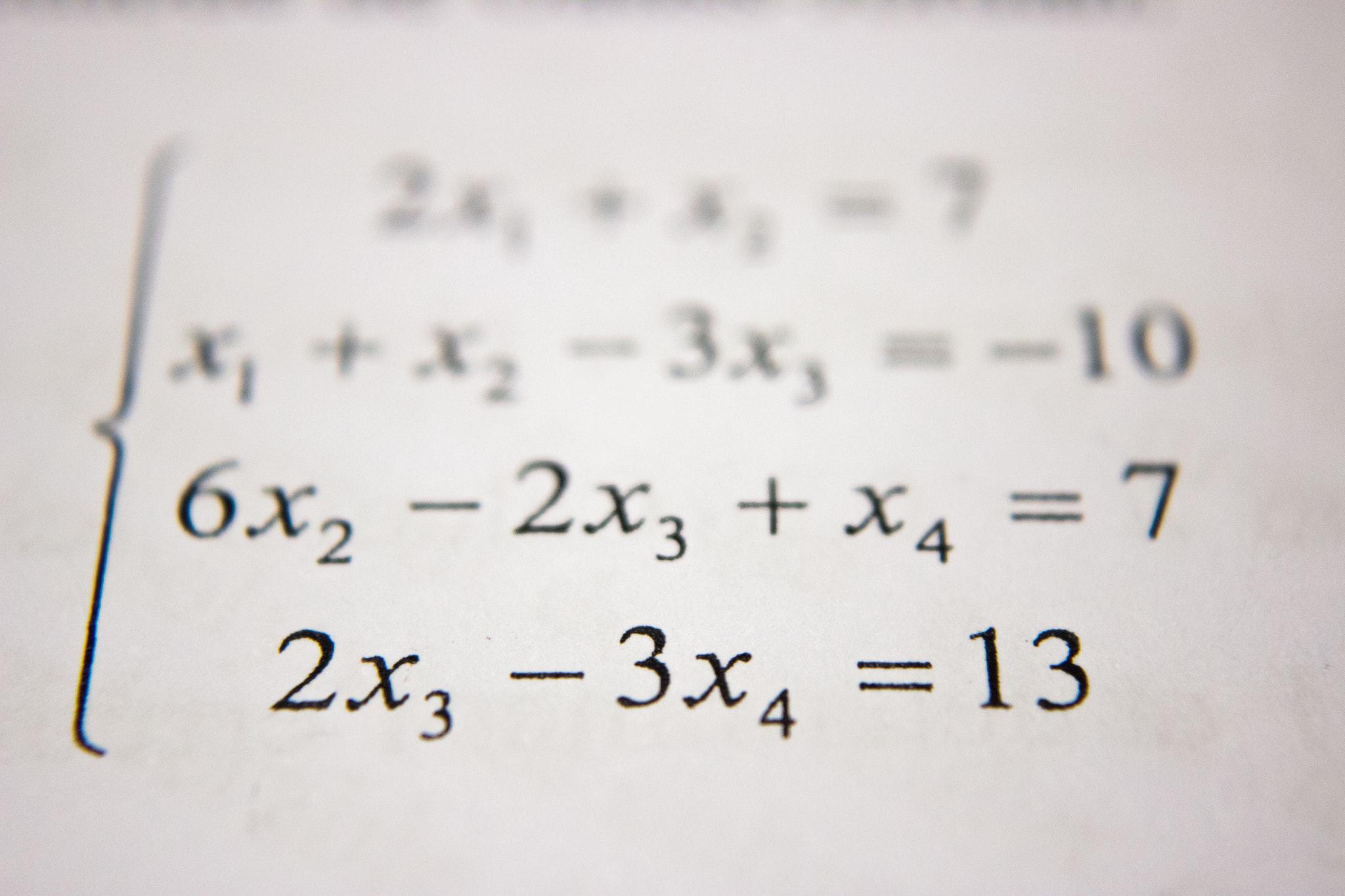Have students lost the ability to do hard math problems?

- Over a period of 30 years, only 43 students passed Lev Landau’s “Theoretical Minimum.”
- The long mathematical journey needed to confront such a test is simply not necessary anymore. Software programs and the internet save all mathematical physicists a lot of time and effort.
- The new approach allows us to explore wider. But does it harm our ability to think deeply about mathematics?
Has the advent of computers as the main tool for hard-core mathematical physics made students stronger or weaker? Before you read any further, you need to know that I just turned 60, which may or may not explain a lot about how I address this question. My age, however, does not make the question itself any less valid. To illustrate my concerns, let me tell you about Theoretical Minimum.
Back in the USSR
In the Cold War era, there was a Soviet theoretical physicist named Lev Landau. To put it mildly, Landau was very, very good. He founded a school that turned out one highly accomplished mathematical physicist after another. The Soviets became renowned for their capacity to see into the heart of complex problems through sheer talent and without computational aids. As part of the school’s curriculum, Landau developed a comprehensive exam called the Theoretical Minimum. This exam was so difficult that over a period of 30 years, only 43 students passed.
When I was a graduate student, we whispered the name “Theoretical Minimum” with the kind of reverence and awe reserved for religious rituals. It was a kind of Mount Olympus that we all hoped, in our own way, we could aspire to climb.
To be honest, there was no way I was ever going to pass something as difficult as Landau’s Theoretical Minimum. Even though I am a theoretical physicist, I just don’t have those kinds of chops. But in the late 1980s, when I was a graduate student, the way we had to learn our craft required us to imagine being able to pass something like Landau’s test. Each week we were given brain-melting problems in electromagnetism, classical mechanics, quantum mechanics, and statistical mechanics, and we had to just… figure them out. If you wanted to, you could spend ten hours in the library hunting for a similar problem in a book or journal and use that for inspiration. But if that path failed, you were stuck.
Losing the mathematical journey
Things are very different now, and I’m honestly not sure whether this is better or worse for today’s students.
Let’s say I give my students a challenging problem in mechanics — one that involves a complicated mathematical technique like Fourier analysis. They can type the problem word for word into Google, and there is a chance they’ll find the solution. They will at least find a solution to a problem much like it. And where the internet falls short, they can use a host of amazing software packages like Mathematica or MATLAB to solve the problem.
Now before you think I’m just an old guy complaining about “these kids today with their fancy computers,” I want you to know that I use the same Google searches and amazing software packages to help me solve my problems. Right now, I’m climbing up the MATLAB learning curve to help me solve a complex set of partial differential equations. The package does in a few minutes what it took me months to program when I was a wee grad student. MATLAB is a godsend.
But there was a power to the old way which I fear we may be losing. That is because the old way was really, really old. Since the time of Pythagoras, 2,500 years ago, mathematics has been done by staring down a problem with a pencil and paper, or a quill and parchment. You were forced to think your way through the silent world of mathematical forms and relationships. There was nothing you could do until your journey led to an insight that you could apply to your problem. With software and the internet, though, there is always something you can do. Press buttons, tweak code, run another search. While the approach saves huge amounts of time and allows a wider exploration, I am afraid that it does not teach the kind of depth of thinking that the Theoretical Minimum was meant to test.
Mourning the abacus
My son is an applied mathematician who works on supply chain dynamics. When I raise this issue with him, he just rolls his eyes. And I get it. I’m sure there were folks who mourned the loss of the abacus. New tools emerge and the world moves on. But as with all things digital, maybe there is a price we are paying for this insane rush into an unknown future — a price high enough that we might want to first pause and ask: “What are we losing, and what do we need to keep?”