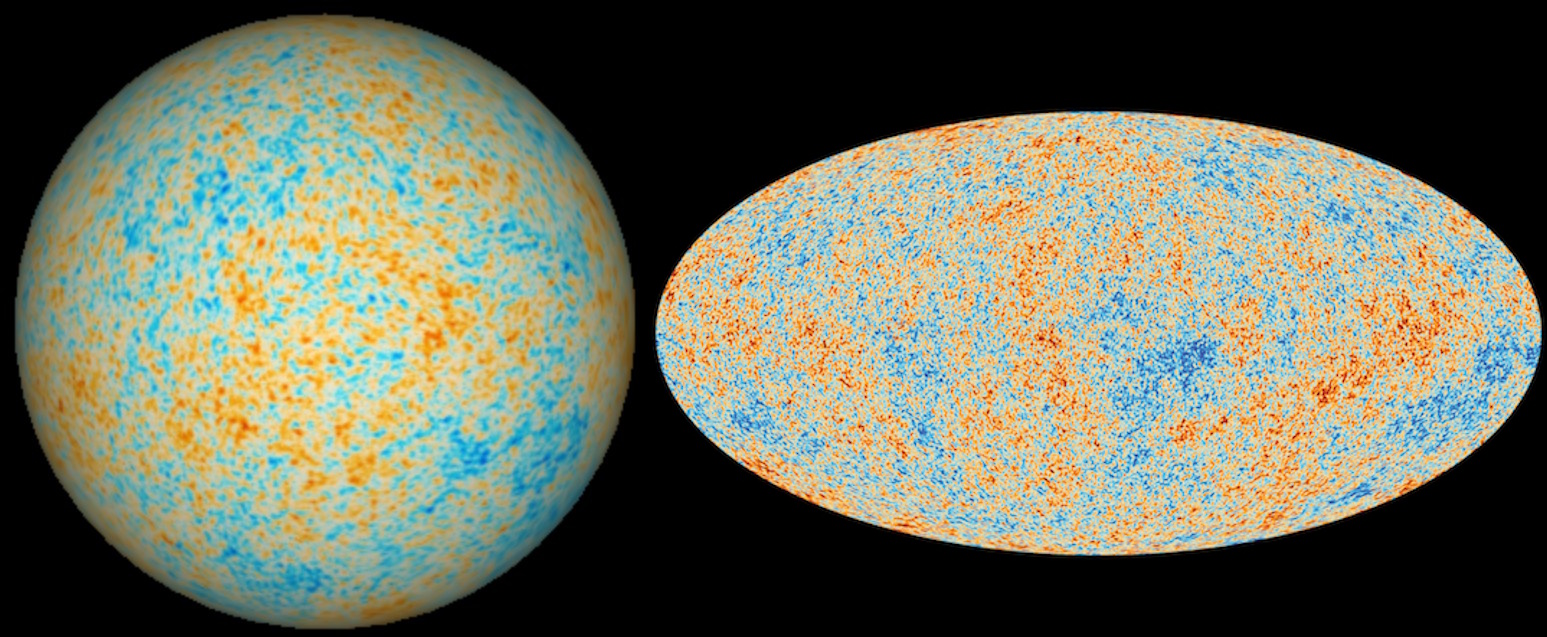Ask Ethan: Why don’t we feel the Universe’s expansion accelerating?

One of the more puzzling and counterintuitive facts about the Universe is that what we experience as space — or the distance/separation between objects — isn’t something that’s fixed over time. Instead, distances evolve, and not in the same way, on cosmic scales, that they evolve here on Earth, in our Solar System, or within our galaxy. Within these more familiar systems, distances tend to change based on the forces acting on the objects in question: specifically, the force of gravity, which works to attract all objects with mass, as well as the electromagnetic and nuclear forces, which tend to dominate on smaller, lower-mass scales.

But on larger cosmic scales, the Universe truly is expanding, and moreover, that expansion is accelerating. Why is this expansion something that we don’t experience in any way here on Earth, and can’t even feel or detect in terrestrial experiments with even our most sensitive instruments? That’s what Jim wants to know, as he writes in to ask:

“Many cosmologists believe that the expansion of the universe is accelerating. If so, why don’t we feel it? I am not convinced [that this must be the case]. We can measure very low gravitational fields. Just how strong is this accelerative force supposed to be? It can push entire galaxies, for example. How strong is that force compared to a weak, but measurable, gravitational field?”

This is a great question, because it gets to the heart of one of the biggest misconceptions about the expanding Universe: the notion that “acceleration implies force.” Let’s dive into the physics at the heart of our cosmos.

Isaac Newton made tremendous advances, largely on his own, across many disciplines of physics and mathematics. He revolutionized gravitation, motion, optics, and co-invented calculus. There was no invocation, nor a need to invoke, anything other than the natural laws of physics for all observed phenomena.

The first physics equation that most people learn isn’t Einstein’s E = mc², even though that’s arguably the most famous equation of all-time. Instead, the first and arguably most important equation that gets to the core of physics goes back to Isaac Newton, and is F = ma, where:

• F is force, and specifically is the net, or total force, acting on an object,
• m is mass, specifically the mass of the object that the force is acting on,
• and a is the acceleration of the object subjected to that force.

It tells you a number of important things that are occurring. It first says that if you have an object that no net force acts on, i.e., where the net force is zero, that object will not accelerate, and instead will remain in constant, unchanging motion: the core idea behind Galilean relativity. It tells you that if there is a net force acting on you, that this force will change your motion, causing an acceleration that’s not only in the direction of the net force, but of a magnitude that equals the magnitude of the force divided by the object’s mass.

And, because it’s an acceleration that’s caused by the force, it tells you that the longer that force remains applied, the more the object’s velocity and distance will both change in the direction in which it accelerates.

When a ball or cylinder begins at rest and then rolls down a hill, the amount of distance that it traverses is proportional to the square of the amount of time it’s been in motion for. This relationship was first uncovered by Galileo more than 400 years ago, and is taken advantage of in the modern-day extreme activity known as “Zorbing.”

This Newtonian picture of reality is extremely successful in many realms: on Earth, on other planets, all throughout our Solar System, in stellar systems outside of our own, and all throughout the galaxy and even beyond. When objects accelerate — that is, when their velocity changes with the passage of time — it’s because there is a net force acting on them, and that force is the cause of their acceleration. And furthermore, the magnitude of the acceleration of that object is given by the magnitude of that net force divided by the accelerating object’s mass. This is true for all of the forces in nature:

• the gravitational force,
• the electromagnetic force,
• the strong nuclear force,
• and the weak nuclear force.

Humans, whenever we jump and our bodies leave the ground, we accelerate downward — toward the center of the Earth — because of the force of gravity from the Earth. The Moon, even though it’s hundreds of thousands of kilometers away from the surface of the Earth, also accelerates “downward,” or toward the center of the Earth, because of the net force acting on it: the force of gravity for the Earth.

However, and this is important, the acceleration of a human near the surface of the Earth and the acceleration of the Moon, some 380,000 km farther away from the surface of the Earth, are not the same. The Moon accelerates much more slowly toward the center of the Earth than a human who jumps — whether from level ground, off of a cliff, or out of an airplane — because the force of gravity gets weaker with greater and greater distances.

This diagram shows the Earth and Moon, as well as the distance between them, to scale. The gravitational force between the Earth and the Moon is proportional to the distance between them squared, which means if the Moon were only half as far away, the gravitational force and the acceleration of the Moon would be quadrupled, but if it were twice as far away, the gravitational force (and hence, the acceleration of the Moon) would be quartered. The Moon is located approximately 60 times farther away from Earth’s center than Earth’s surface is.

In fact, this is true of all of the fundamental forces of nature: the greater the distance is between any two objects that there’s a force (or interaction) between, the weaker the strength of the force (or interaction) becomes. In fact, if the Moon were:

• only half as far away from the Earth, the gravitational force acting on it would be quadrupled,
• twice as far away from the Earth, the gravitational force acting on it would be quartered,
• ten times as far away from the Earth, the gravitational force acting on it would be just one-hundredth (or 1%) of what it is at present,

and as the force changed, because the Moon’s mass is unchanging, so too would its acceleration toward the center of the Earth change in the same fashion.

However, we’ve sent astronauts to the Moon itself, and had them both orbit around the Moon as well as land and walk on its surface. Despite how great the gravitational force of the Earth is, and despite the fact that the Moon actually changes its distance from Earth substantially, an astronaut on the Moon doesn’t “feel” the gravitational force from the Earth at all. There is no experiment or measurement they can perform — from dropping feathers and hammers to moving their bodies to conducting studies of motion using high-tech accelerometers — that allows them to detect the Earth’s gravitational force acting on them.

The Lunar Roving Vehicle was included on the last three Apollo missions and enabled the astronauts to travel greater distances and explore more diverse regions of the Moon than they were able to on foot alone. The tracks of these vehicles are still present today, and can be seen in data from the Lunar Reconnaissance Orbiter. The gravitational effects of Earth cannot be felt by astronauts on the Moon.

There is a reason for this. From the point of view of an astronaut on the Moon, the “laboratory” of being on the Moon is itself an inertial frame of reference. Sure, the Earth tugs on the Moon, just as surely as the Sun and the other planets also gravitationally tug (and exert a force) on the Moon, but remember what Newton’s equation, F = ma, actually tells us. It tells us that, while the force on an object is proportional to its mass, the acceleration of that object is not: the acceleration is actually the force on that object divided by its mass: a = F/m. When the Earth pulls on an astronaut on the Moon, it exerts a smaller force on the astronaut than it exerts on the Moon, but the force is smaller in proportion to the astronaut’s mass.

In other words, the Earth causes the astronaut to accelerate by the exact same amount that it causes the Moon to accelerate. Similarly, the Sun (and all of the other planets besides Earth) also cause both the Moon and an astronaut on the Moon to accelerate at the same rate, even though the forces on them are vastly different. Because both the astronaut and the Moon are accelerated uniformly — i.e., at the same rate — by the external forces acting on them, an astronaut on the Moon only experiences the gravitational force of the Moon itself in terms of the net force acting on it. Similarly, once any object is dropped, including the famous hammer and feather experiment performed during Apollo 15, it’s the force of the Moon’s gravity, not influenced by the Earth, Sun, or anything else, that determines the rate at which those objects accelerate downward and fall.

The reason this notion of F = ma is so successful on the scales that humans experience, including on terrestrial, Solar System, celestial, and even galactic scales, is that we are restricting ourselves to considering systems that are bound together by one of the fundamental forces. (In fact, in all of the cases that we’ve considered here, that force is the gravitational force.)

But this is no longer true on cosmic scales.

There are important assumptions that normally go unstated whenever we talk about Isaac Newton and a Newtonian view of the Universe. In particular, Newton assumed that:

• forces rule the entire Universe,
• that the gravitational force was instantaneous,
• that it acted “at a distance” between objects, and that distance was some value that could be known in an absolute and objective fashion,
• and that it occurred between all objects that had a mass.

All of these assumptions, as true as they seem, were overturned once Einstein came along. Gravitation can be viewed as a force under many circumstances, but it’s also more than a force: it’s a consequence of the fact that mass-and-energy (not just mass) curve the fabric of spacetime itself and cause that fabric to evolve, and then that curved, evolving fabric tells matter-and-energy how to move. The gravitational force isn’t instantaneous, but only propagates at a finite speed: the speed of light. And “distance” is not absolute, but is rather relative, as objects in motion experience and measure distances to be contracted along the direction of motion relative to objects that are instead at rest.

The gravitational behavior of the Earth around the Sun is not due to an invisible gravitational pull, but is better described by the Earth falling freely through curved space dominated by the Sun. The shortest distance between two points isn’t a straight line, but rather a geodesic: a curved line that’s defined by the gravitational deformation of spacetime. The notion of “distance” and “time” is unique for every observer, but under Einstein’s description, all frames of reference are equally valid, and the “spacetime interval” remains an invariant quantity.

These realizations led humanity to abandon this wholly Newtonian concept of forces and accelerations as being linked by F = ma, at least under all circumstances. Instead, a more universally acceptable concept is given by Einstein’s general theory of relativity, which relates the concept of spacetime, which can be curved and can evolve in many ways — including by either expanding or contracting — to the distribution and motion of the masses and other quanta and forms of energy present within that spacetime.

When things are approximately Newtonian, such as when you have a gravitationally bound system that you’re considering with masses moving at speeds slow compared to the speed of light and where there are no extremely dense concentrations of matter (including black holes and neutron stars), then it makes sense to use F = ma, as Newton’s conception of reality comes very, very close to producing exactly the same predictions as Einstein’s much more labor-intensive predictions.

This approximation works very well on scales of planets, stellar systems, stars, individual galaxies, and even isolated groups and clusters of galaxies. The largest such system that we’re a part of is our Local Group of galaxies, which includes the Milky Way, Andromeda, and more than 100 other, smaller galaxies all bound together. The Local Group extends for approximately 5 million light-years, and when objects within this group of galaxies accelerate relative to one another, it’s because of a gravitational force. That is something we can measure and quantify, no doubt.

This illustration of our Local Group, which contains the Milky Way (at left), showcases how there are between 30-100 known small, low-mass galaxies for every large galaxy like the Milky Way or Andromeda in our modern-day Universe. Most of the stars are found in large, massive galaxies, but most galaxies are small and seemingly insignificant.

But the expansion of the Universe — once you go to scales larger than that of a gravitationally bound structure — is not a Newtonian construct, and no longer obeys the notion of F = ma. This is a phenomenon that is exclusive to general relativity, and arises whenever you have a system that obeys the Einstein Field Equations under conditions where the energy within your system is (roughly) uniformly distributed all throughout space. No longer are accelerations, where you can measure the change in the speed of a distant object over time, determined by forces, but instead whether an object accelerates or not, as well as how quickly it accelerates or decelerates, is determined by all of the different types of energy present within your Universe.

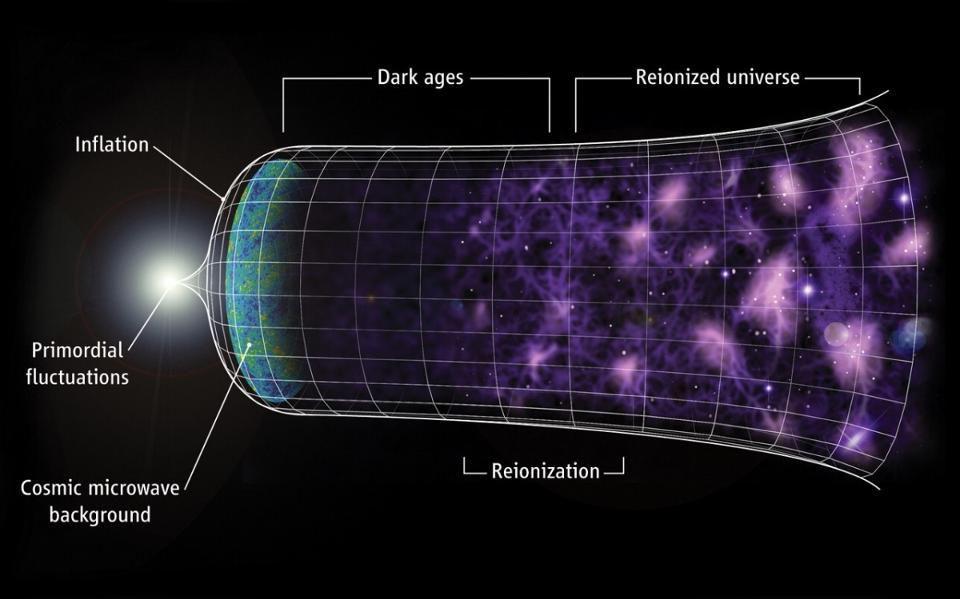
In our Universe, we can measure how quickly distant objects appear to be receding from us, as we can infer a recessional velocity from the observed redshift of those objects. We can see how the redshift-distance relation behaves as we look to more and more distant objects, giving us a clue to how the Universe’s expansion rate has evolved over time. And we can use a variety of cosmic probes to determine what the various forms (and densities) of energy within the Universe are. When we put this all together, we arrive at a consistent picture of our own cosmic history, complete with an understanding of what the Universe is made out of: both now, as well as at all moments in our cosmic past.

The relative importance of different energy components in the Universe at various times in the past. Dark matter has been largely important for extremely long cosmic times, and we can see its signatures in even the Universe’s earliest signals. Meanwhile, radiation was dominant for the first ~10,000 years of the Universe after the Big Bang. Note that in the future, when dark energy reaches a number near 100%, the energy density of the Universe (and, therefore, the expansion rate) will remain constant arbitrarily far ahead in time.

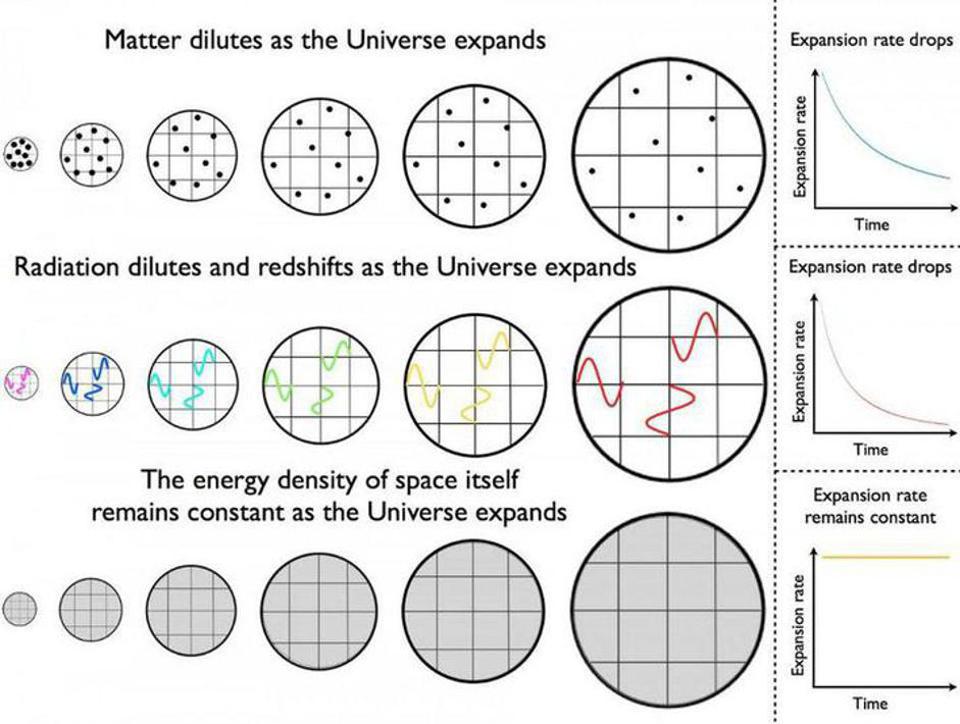
Today, our Universe is dominated by dark energy: a novel form of energy whose nature is ultimately unknown, but that appears to be most consistent with a cosmological constant, or a form of energy that’s inherent and intrinsic to space itself. This is important, because it’s the sum total of all the different forms of energy that tells us how the Universe expands, and how those different forms of energy evolve over time tells us how the distances between two unbound objects as well as the inferred recession speeds between those objects will evolve over time. There are three classes of energy in the Universe that are important for these purposes.

1. There’s radiation, or particles that move at or near the speed of light, which includes photons and neutrinos. As the Universe expands, the number density of these particles drops proportionally to the volume of the Universe (i.e., as size/distance cubed) multiplied by another factor of size/distance as the wavelength of the radiation gets stretched within the expanding Universe as well.
2. There’s matter, including normal and dark matter, whose density drops proportionally only to the volume of the Universe: as size cubed.
3. And finally, there’s dark energy, which we assume to be a cosmological constant (although that may only be approximately true), whose density remains constant over time.

In a Universe that contains all three, there will be three stages to any expanding Universe: an early, radiation-dominated stage, where the expansion rate drops quickly over time, a middle stage dominated by matter, where the expansion rate still drops over time but not as quickly as during radiation domination, and then a final stage of dark energy domination, where the expansion rate ceases to drop, and instead remains at a finite, positive, non-zero value.

While matter and radiation become less dense as the Universe expands owing to its increasing volume, dark energy is a form of energy inherent to space itself. As new space gets created in the expanding Universe, the dark energy density remains constant.

The implications of a Universe exhibiting this behavior — with radiation, matter, and dark energy within it — are profound. It means that the expansion rate, which we measure as a speed (kilometers-per-second) per unit distance (per megaparsec), or in terms of km/s/Mpc, will drop when radiation and matter are dominant, but will only approach a constant positive value when dark energy is dominant. And it means that the inferred recession speed of a distant, unbound galaxy (in terms of km/s), is dependent both on the expansion rate at any moment in time (in terms of km/s/Mpc) and also on the distance to that galaxy (measured in Mpc).

When radiation and matter are dominant, the observed recession speed goes down over time, and so we say the expansion decelerates, because the speed at which the galaxy appears to be moving away from us, in terms of km/s, appears to be going down over time, or dropping. But when dark energy is the dominant factor in causing the Universe to expand — something that first happened about 6 billion years ago — the observed recession speed goes up over time, as the speed at which a distant, unbound galaxy recedes from us appears to increase with time. Even though the expansion rate isn’t increasing, the recession speed appears to go up as the distance to the galaxy increases, and so we say the expansion accelerates.

But don’t fall for a common misconception: this cosmic acceleration is not the consequence of a force! It is a consequence of the presence of dark energy — a form of energy inherent to space itself — within the expanding Universe. The reason it wasn’t discovered until the 1990s is because we cannot measure it in a laboratory here on Earth, but only by looking to the extremely distant galaxies present throughout the visible Universe. On cosmic scales, we can still have acceleration, but we can no longer chalk any of it up to the classic F = ma given to us by Isaac Newton back in the 17th century!

Send in your Ask Ethan questions to startswithabang at gmail dot com!