Why does our Universe have 8 types of gluon?
- In our Universe, protons and neutrons are held together by the strong force: where quarks exchange gluons, and gluons mediate the strong nuclear force.
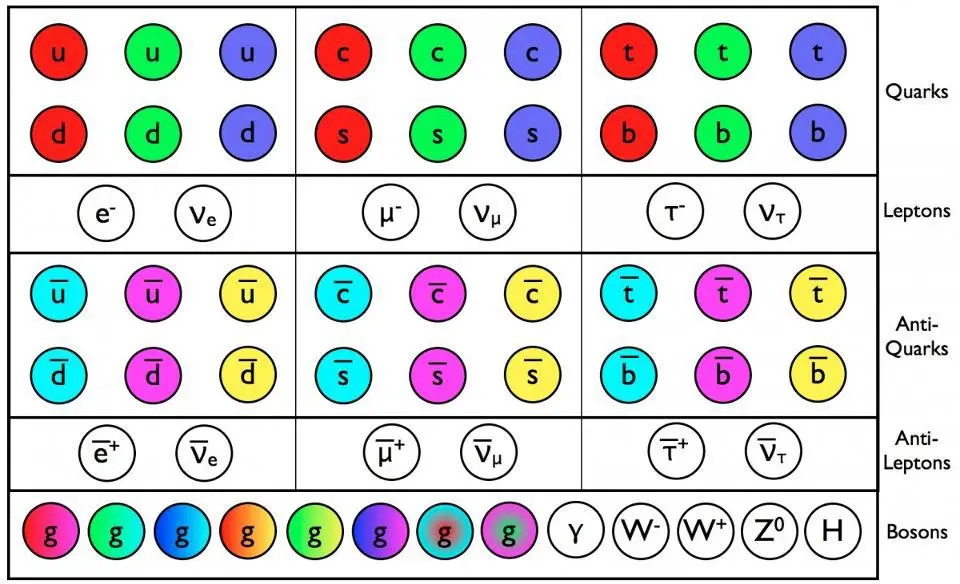
- But quarks (and antiquarks) can have 3 colors (and anticolors), while each gluon is a combination of a color and an anticolor.
- So why aren’t there 9 gluons? Why are there only 8? The reason is subtle, but with a little bit of thought, even us non-physicists can understand why.
One of the most puzzling features of the Universe is the strong nuclear force. Inside every proton or neutron-like particle, there are three quarks, each of which has their own color. All three colors combined add up to a colorless combination, which the Universe seems to mandate. You can either have three quarks, three antiquarks (with corresponding anticolors), or a quark-antiquark combination: with colors-anticolors that cancel out. More recently, tetraquarks (with two quarks and two antiquarks) and pentaquarks (with four quarks and one antiquark) have been found to also produce colorless quantum states.
But despite the fact that there are three colors and three anticolors allowed in nature, the particles that mediate the strong force — the gluons — only come in eight varieties. You might think that every color-anticolor combination that you can dream up would be allowed, giving us nine, but our physical Universe plays by different rules. Here’s the incredible and surprising physics of why we only have eight gluons.

In physics, there are only a few fundamental forces, each governed by their own rules. In gravitation, there’s only one kind of charge: mass/energy, which is always attractive. There’s no upper limit to how much mass/energy you can have, as the worst you can do is create a black hole, which still fits into our theory of gravity. Every quantum of energy — whether it has a rest mass (like an electron) or not (like a photon) — curves the fabric of space, causing the phenomenon we perceive as gravitation. If gravitation turns out to be quantum in nature, there’s only one quantum particle, the graviton, required to carry the gravitational force.
Electromagnetism, the other fundamental force that readily appears on macroscopic scales, gives us a little more variety. Instead of one type of charge, there are two: positive and negative electric charges. Like charges repel; opposite charges attract. Although the physics underlying electromagnetism is very different in detail than the physics underlying gravitation, its structure is still straightforward in the same way that gravitation is. You can have free charges, of any magnitude, with no restrictions, and there’s only one particle required (the photon) to mediate all the possible electromagnetic interactions.

But when we move on to look at the strong nuclear force, the rules become fundamentally different. Instead of one type of charge (gravitation) or even two (electromagnetism), there are three fundamental charges for the strong nuclear force, known as colors. In addition, colors obey different rules than the other forces. They include the following:
- You cannot have a net charge of any type; only “colorless” states are allowed.
- A color plus its anticolor is colorless; additionally, all three unique colors (or anticolors) added together is colorless.
- Each quark contains a net color charge of one color; each antiquark has an anticolor assigned to it.
- The only other Standard Model particle with a color is the gluon: quarks exchange gluons, and that’s how they form bound states.
Although these are some complicated rules that are very different from the rules for gravitation and electromagnetism, they actually help us understand how individual particles like protons and neutrons are held together.
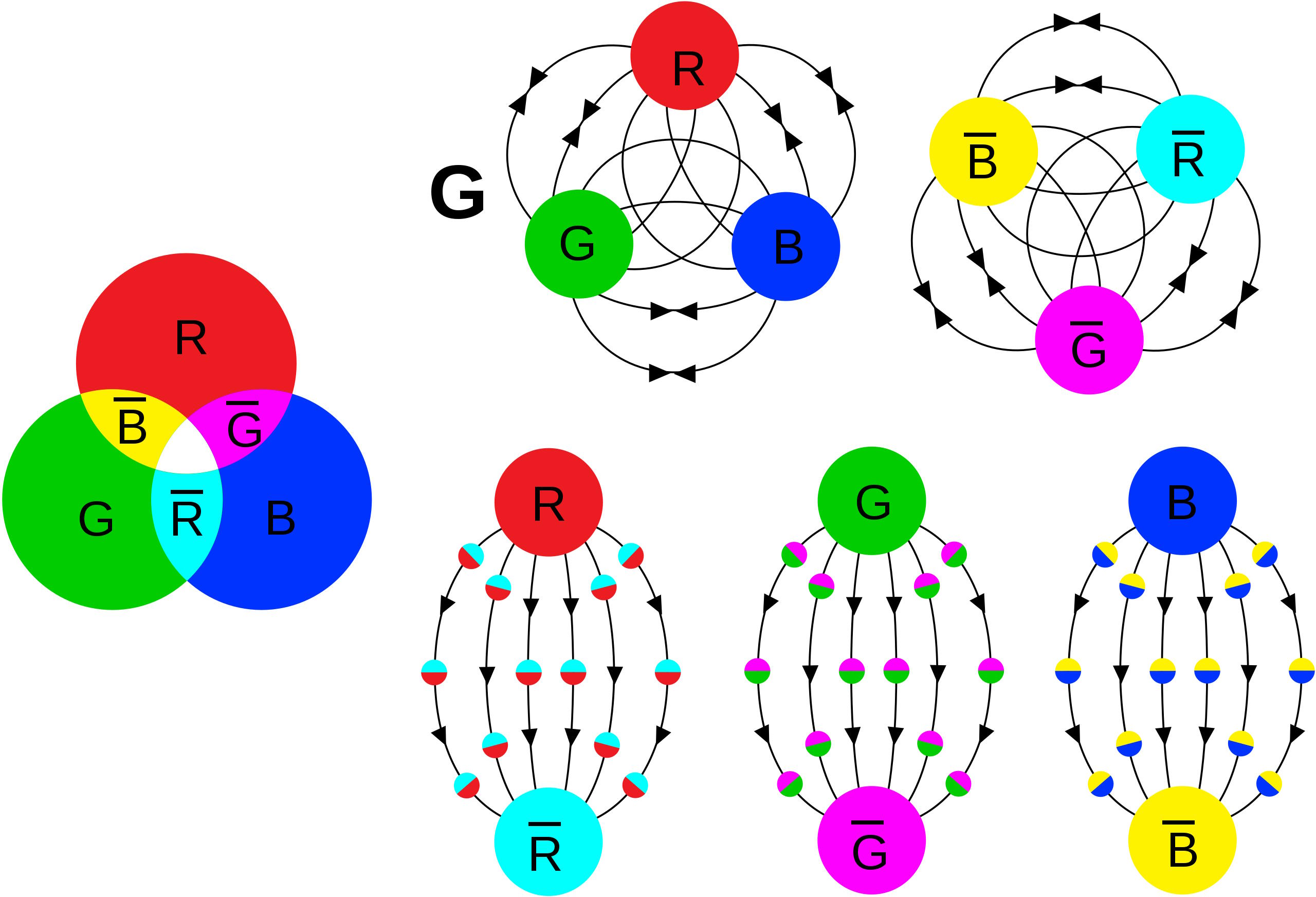
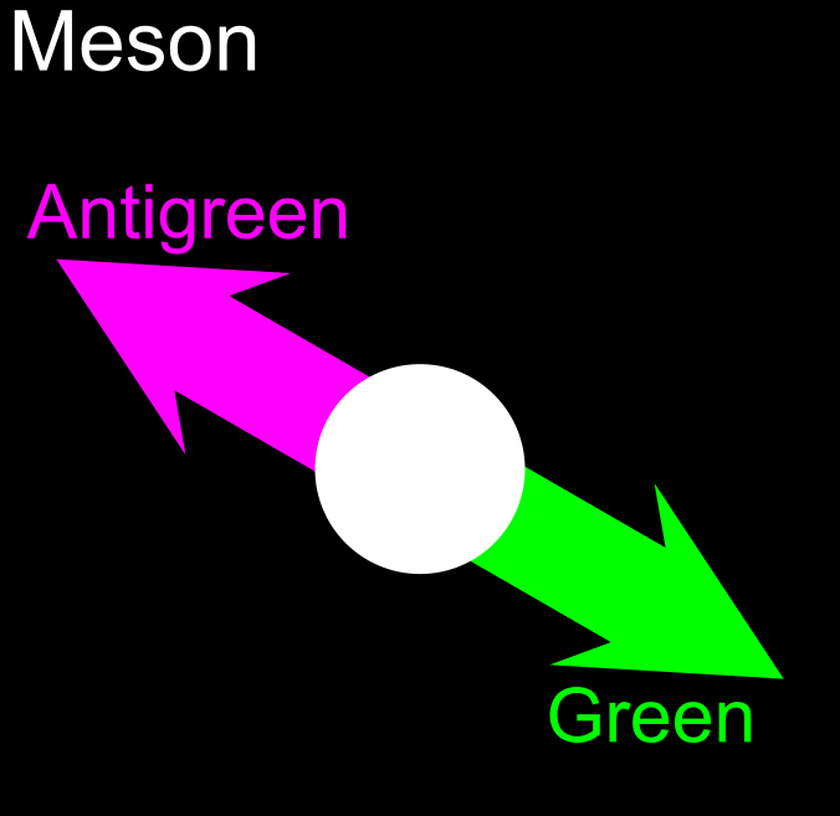
First off, protons and neutrons themselves — and other particles like them, called baryons — must be composed of three quarks, each possessing a different color. For every particle like a proton or neutron, there’s an antiparticle counterpart, made up of three antiquarks, each of which contains a different anticolor. Every combination that exists at every moment in time must be colorless, which means one red, one green, and one blue color for the quarks; one cyan (anti-red), one magenta (anti-green), and one yellow (anti-blue) anticolor for the antiquarks.
Like all particles governed by a quantum field theory, the strong nuclear force works through the exchange of particles. Unlike gravitation or electromagnetism, however, the structure of the theory behind the strong nuclear force is a bit more complicated. Whereas gravitation itself doesn’t change the mass/energy of the particles involved, and electromagnetism doesn’t change the electric charge of the particles attracting or repelling one another, the colors (or anticolors) of the quarks (or antiquarks) change every time the strong nuclear force occurs.

The way we visualize this is through the exchange of gluons. Every gluon will be emitted by one quark (or antiquark) and absorbed by another quark (or antiquark), which is the same rule that electromagnetism follows: every photon is emitted by one charged particle and absorbed by another. The photon is the force-carrying particle that mediates the electromagnetic force; the gluons are the particles that mediate the strong nuclear force.
You might imagine, right away, that there are nine gluons that are possible: one for each of the color-anticolor combinations possible. Indeed, this is what almost everyone expects, following some very straightforward logic. There are three possible colors, three possible anticolors, and each possible color-anticolor combination represents one of the gluons. If you visualized what was happening inside the proton as follows:
- a quark emits a gluon, changing its color,
- and that gluon is then absorbed by another quark, changing its color,
you’d get an excellent picture for what was happening with six of the possible gluons.
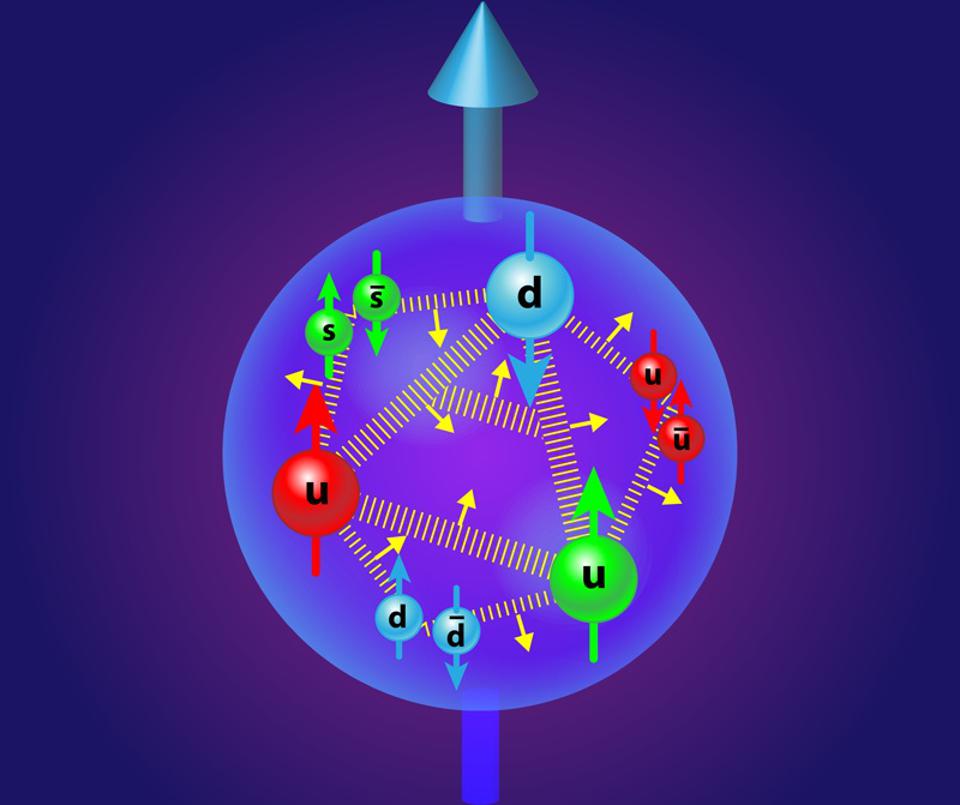
If, inside your proton, you had three quarks — one red, one green, and one blue, summing up to colorless — then it’s pretty clear that the following six gluon exchanges could occur.
- the red quark could emit a red-antiblue gluon, turning it blue and turning the blue quark red,
- or a red-antigreen gluon, turning it green while turning the green quark red,
- or the blue quark could emit a blue-antired gluon, turning it red with the red quark becoming blue,
- or a blue-antigreen gluon, turning it green while the green quark becomes blue,
- or the green quark could emit a green-antired gluon, turning it red with the red quark turning green,
- or a green-antiblue gluon, turning it blue with the blue quark becoming green.
That takes care of the six “easy” gluons. But what about the other ones? After all, wouldn’t you expect there to be a red-antired, a green-antigreen, and a blue-antiblue gluon as well?

Unfortunately, no. Let’s say you did: let’s say you had a red-antired gluon. A red quark would emit it, remaining red. But which quark is going to absorb it? The green quark can’t, because there isn’t an “antigreen” part to cancel it out and turn it to colorless, so it can pick up the red from the gluon. Similarly, the blue quark can’t, because there’s no “antiblue” in the gluon.
Does that mean there are only six gluons, and the other three can’t physically exist?
Not quite. While you can’t have a pure “red-antired” or “green-antigreen,” you can have a mixed state that’s part red-antired, part green-antigreen, and even part blue-antiblue. This is because, in quantum physics, particles (or particle combinations) with the same quantum states all mix together; it’s unavoidable. Just as the neutral pion is a combination of up-antiup and down-antidown quarks, the other allowable gluons are combinations of red-antired, green-antigreen, and blue-antiblue.
But there aren’t three of them, either. The key reason is this: because of the specific properties of the strong force, there’s one more constraint. Whatever you have as a (positive) color-anticolor combination for a single color, you need a negative color-anticolor combination of a different color in order to have a physically real gluon.
Let’s show you what this looks like with an example. Say you want a gluon that has both red-antired and blue-antiblue properties. (The actual color choices themselves are arbitrary.) You can do that, but the combination you’ll need is:
- [(red-antired) — (blue-antiblue)]/√(2),
which has a negative sign in there. Now, you want another gluon, but it has to be independent of the combination you already used. That’s okay; we can write one down! It looks like this:
- [(red-antired) + (blue-antiblue) — 2*(green-antigreen)]/√(6).
Is there a third combination we can write down that’s independent of both of these combinations?

Well, yes, but it violates the other important rule we just talked about. You could write down a third gluon of the following form:
- [(red-antired) + (blue-antiblue) + (green-antigreen)]/√(3),
which is independent of both of the previous two combinations. In other words, if this were allowable, we’d have a ninth gluon! But, as you might’ve guessed, that’s not the case at all. All of the color-anticolor components are positive; the negative color-anticolor combination isn’t there, which corresponds to this hypothetical gluon not being physical. For three possible color-anticolor combinations, you can only have two independent configurations that have minus signs in them; the third will always be positive.
In group theory terms (for those of you advanced enough in physics or math), the gluon matrix is traceless, which is the difference between the unitary group, U(3), and the special unitary group, SU(3). If the strong force were governed by U(3) instead of SU(3), there would be an extra, massless, completely colorless gluon, a particle which would behave like a second photon! Unfortunately, we only have the one type of photon in our Universe, teaching us experimentally that there are only 8 gluons, not the 9 you might expect. (Or, if you want to drive a mathematician nuts, because even though 3 × 3 = 9, the specific kind of multiplication we’re dealing with states that 3 ⊗︀ 3 = 8 ⊕ 1, and that “1” is physically forbidden here.)
With three colors and three anticolors for the quarks and antiquarks, it’s these combinations of color-anticolor particles that mediate the strong nuclear force between them: the gluons. Six of the gluons are straightforward, with a color-anticolor combination that’s has a different anticolor from the color in question. The other two are combinations of colors-anticolors mixed with one another and a minus sign between them. The only other allowable combination is colorless, and that fails to meet the criteria necessary to be a physical particle. As a result, there are only 8.
It’s remarkable that the Standard Model is so well-described by the mathematics of group theory, with the strong force perfectly aligning with the predictions of that particular branch of mathematics. Unlike gravitation (with only one type of attractive, positive charge) or electromagnetism (with positive and negative charges that attract or repel), the properties of color charge are far more intricate, yet are thoroughly understandable. With just eight gluons, we can hold together every physically possible combination of quarks and antiquarks spanning the entire Universe.