Throwback Thursday: Why the Sun Shines, from Inside-to-Out

The Sun — like nearly all stars — burns bright through its nuclear reactions, sending light, heat and energy out into the Universe over a timespan of billions of years. But how?

“The sun is a miasma
Of incandescent plasma
The sun’s not simply made out of gas
No, no, no
The sun is a quagmire
It’s not made of fire
Forget what you’ve been told in the past” -They Might Be Giants

(Each Thursday, we take a classic post from the Starts With A Bang archives and update, augment and enhance it for our Throwback Thursday series. Welcome!)

It’s so ingrained in us that the Sun is a nuclear furnace powered by hydrogen atoms fusing into heavier elements that it’s difficult to remember that, just 100 years ago, we didn’t even know what the Sun was made out of, much less what powered it!

From the laws of gravity, we’ve known for centuries that it had to be around 300,000 times the mass of Earth, and from measurements of the energy received here on Earth, we knew how much energy it releases: 4 × 10^26 Watts, or about 10^16 times as much as the most powerful power plants on our planet.

But what wasn’t known was where it got its energy from. No less a figure than Lord Kelvin set out to tackle that question.

From the recent work of Darwin, it was evident that the Earth needed at least hundreds of millions of years for evolution to produce the diversity of life we see today, and from contemporary geologists, the Earth had apparently been around for at least a couple of billion years. But what type of power source could be that energetic for that long a period of time? Lord Kelvin — the famed scientist who discovered absolute zero — considered three possibilities:

1. ) That the Sun was burning some type of fuel.
2. ) That the Sun was feeding on material from within the Solar System.
3. ) That the Sun generated its energy from its own gravity.

Let’s take a look at each of these.

1.) That the Sun was burning some type of fuel. The first possibility, that the Sun burned some type of fuel source, made a lot of sense.

Given that we now know the Sun is mostly made up of hydrogen, and how easily hydrogen combusts here on Earth, it seems very straightforward that burning such a giant store of hydrogen could provide a tremendous amount of energy. Indeed, if the Sun were made entirely out of hydrogen, and we considered that hydrogen fuel combusted the exact same way that it does here on Earth, there would be enough fuel for the Sun to produce that incredible amount of power — 4 × 10^26 Watts — for tens of thousands of years only. Unfortunately, even though that’s quite long when compared to, say, a human lifetime, it’s not nearly long enough to account for the long history of life, Earth, or our Solar System. Kelvin, therefore, was able to rule this first option out.

2.) That the Sun was feeding on material from within the Solar System. The second possibility was a little more intriguing. While it wouldn’t be possible to sustain the Sun’s power output from whatever hydrogen atoms were presently in there, it could be possible in principle to continuously add some type of fuel to the Sun to keep it burning. It was well-­known that comets and asteroids abound in our Solar System, and so long as there was enough new (unburned) fuel being added to the Sun at a roughly steady rate, its lifetime could be extended by large amounts.

However, you couldn’t add an arbitrary amount of mass, because at some point, the increasing mass of the Sun would slightly change the orbits of the planets, which had been observed to incredible precision since the 16th Century and the time of Tycho Brahe. A simple calculation showed that even just adding a small amount of mass to the Sun — less than a thousandth of a percent over the past few centuries — would have a measurable effect, and that the steady, observed elliptical orbits ruled this option out. So, Kelvin reasoned, that left option #3.

3.) That the Sun generated its energy from its own gravity. The energy released could have been powered by the Sun’s gravitational contraction over time. In our common experience, a ball raised to a certain height on Earth and then released will pick up speed and kinetic energy as it falls, and that gets converted to heat (and deformation) when it collides with the Earth’s surface and comes to rest. Well, that same type of initial energy — gravitational potential energy — causes molecular clouds of gas to heat up as they contract and become denser.

Moreover, because these objects are now much smaller (and more spherical) than they were back when they were diffuse gas clouds, it will take a long time for them to radiate all of that heat energy away through their surface. Kelvin was the foremost expert in the world on how the mechanics of how this would happen, and the Kelvin­-Helmholtz mechanism is named after his work on this subject. For an object such as the Sun, Kelvin calculated, it’s lifetime for emitting as much energy as it does would be on the order of tens of millions of years: somewhere between 20 and 100 million years to be more precise.

Of course, we now know that our Solar System is on the order of 4.5 billion years old, and that none of Kelvin’s answers were quite right. The third option is actually how white dwarfs are powered, why they are so small (the mass of the Sun confined in a volume the size of Earth) and shine dimly for many trillions of years. And Kelvin’s reasoning for ruling out the first and second options are still valid.

There was one thing he didn’t know, however: there was a new kind of fuel.

The same reaction that powers the hydrogen bomb shown here — nuclear fusion — also powers the Sun and all main-sequence stars! That is to say, the vast majority of stars in the night sky burn hydrogen in their core and all true (non-brown-or-white-dwarf) stars that are visible from Earth once fused hydrogen into helium in their interiors.

But how does this happen? It’s actually an amazing story, with many caveats that you might not expect. Let’s begin in our Solar System, at the planets we’re familiar with.

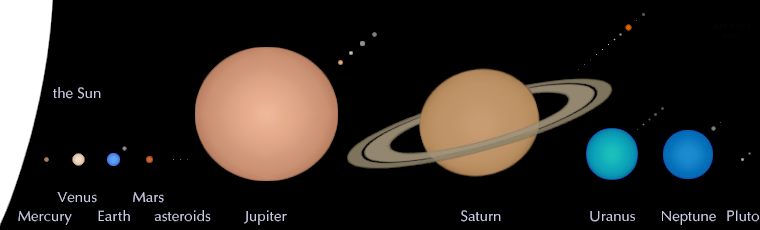
It should come as no surprise that Mercury, the smallest planet, is the least massive, and that Jupiter, the largest planet, is the most massive. But what might be suprising is that Saturn, our Solar System’s second largest planet, is nearly the size of Jupiter, at 85% its diameter. But despite that comparable size, it’s only one third the mass of its Jovian superior!

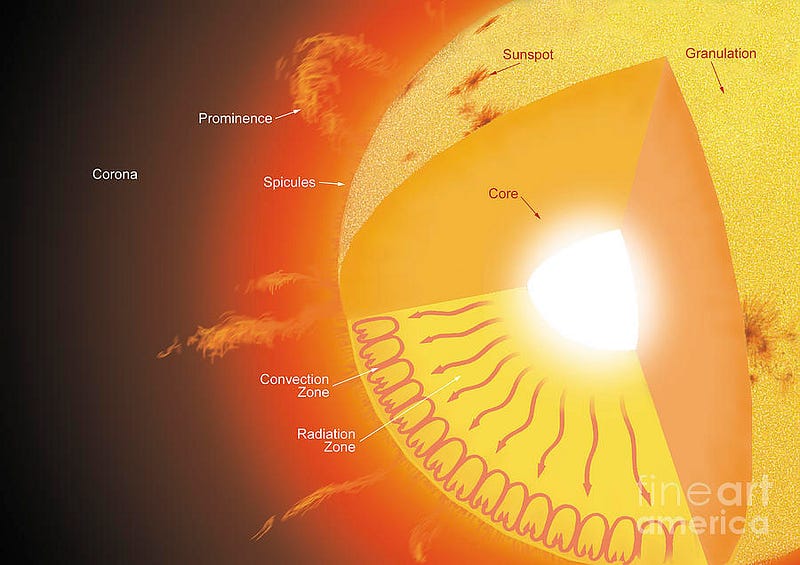
The key to understanding why this happens — and how the Sun (and all stars) shine — is to go down to the atomic level.

It’s not, as you might expect, that the two world are made out of significantly different atoms; they’re not. It’s that Jupiter and Saturn are made out of nearly identical stuff, but Jupiter really has about three times as much of it as Saturn does. The big difference is that Jupiter has so much mass that the atoms themselves start to compress one another at the center, packing them tighter and tighter together as more mass accumulates.

This has gotten really fascinating as we’ve discovered planets outside the Solar System, because as planets get much more massive than Jupiter, they start to get even smaller in size.

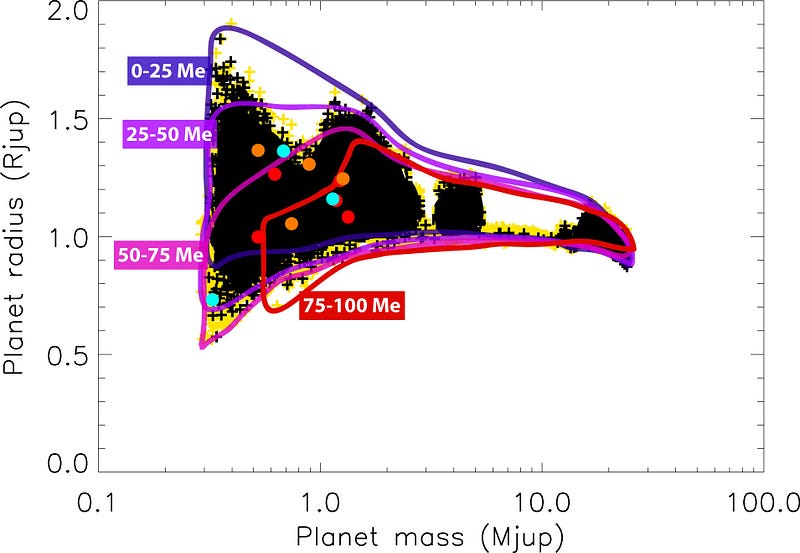
As you make your object more and more massive, it continues to shrink and shrink. By time your planet is about 70 times as massive as Jupiter — or about 8% as massive as the Sun — the hydrogen atoms at the core are so dense and under so much pressure that they can actually begin fusing together into heavier elements!

And when that happens, your “too-big-to-be-a-planet” mass expands. When you were just a planet, gravity pulls inwards on all of your atoms, attempting to collapse them down to as small a space as possible, but the atoms themselves can resist it. But once you achieve too great a density at too high a pressure, and fusion starts, you begin turning mass into energy.

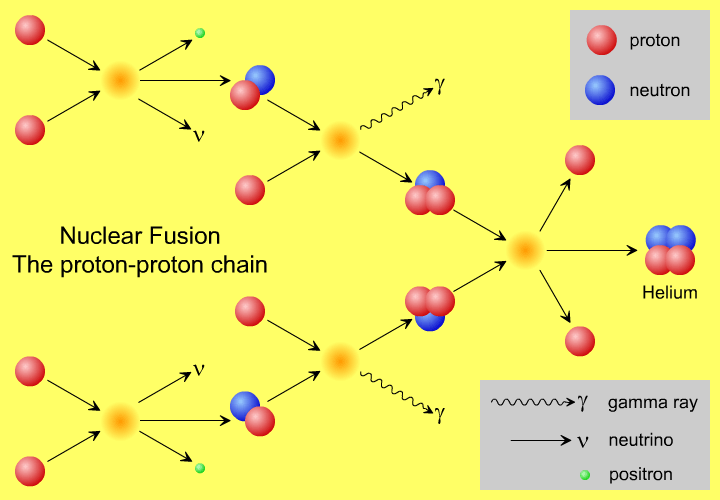
But it probably doesn’t happen the way you think. You probably have a vision in your head similar to the picture above, of protons smashing into one another and fusing together, up a chain, into heavier elements. Yet, that’s not quite right, not even in our Sun.

A core temperature of 15,000,000 K — which is what we achieve in our Sun’s core — means a mean energy of 1.3 keV per proton. But the distribution of these energies is Poisson, meaning that there is a small probability of having protons with extremely high energies, and speeds rivaling the speed of light. With 10^57 protons (of which maybe a few times 10^55 are in the core), I get the highest kinetic energy a proton is likely to have is about 170 MeV. This is almost (but not quite) enough energy to overcome the Coulomb barrier between protons.

But we don’t need to overcome the Coulomb barrier completely, because the Universe has another way out of this mess: quantum mechanics!

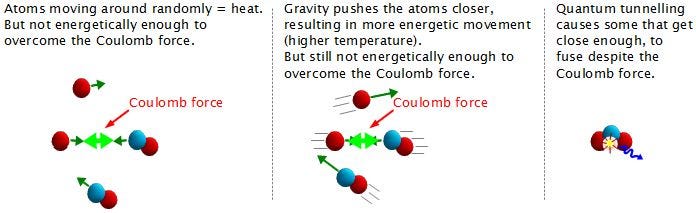
The individual protons in a star’s core might not have enough energy to overcome the repulsive force caused by their electric charges, but there’s always a chance that these particles can undergo quantum tunneling, and wind up in a more stable bound state (e.g., deuterium) that causes the release of this fusion energy. Even though the probability of quantum tunneling is very small for any particular proton­-proton interaction, somewhere on the order of 1­-in­-10^28 — or the same as your odds of winning the Powerball lottery three times in a row — the fact that there are so many interactions in the core happening continuously means that a whopping
4 × 10^38 protons fuse into helium every second in our Sun.

And this process, of nuclear fusion fueled by quantum physics, is what’s responsible for powering the vast majority of stars. Once you’ve got it, what does this energy — in the form of radiation — do?

It pushes outwards. Rather than atoms holding up a star against gravity, it’s now the radiation from the nuclear fusion you began. A low-mass star like a Red Dwarf is many times larger than Jupiter, while a star as massive as the Sun is significantly larger still.

A G-type star like our Sun may live from 10-15 billion years, while a low-mass, dim red dwarf star (an M-star) may live anywhere from hundreds of billions to many trillions of years, far longer than the age of the Universe!

But on the other side, as you get more and more massive, your fusion-burning core gets progressively larger and larger. The largest, bluest O-stars weigh in at more than 100 times the mass of our Sun, and burn through their entire complement of hydrogen fuel in less than onemillion years!

Amazingly, for all hydrogen-burning stars like our Sun, the only major determinant for the star’s lifetime is its mass.

So even though it might not look it, the reason the Sun burns its fuel at the rate it does is because this is the right rate for its mass. Given that nuclear fusion produces the radiation necessary to cancel out the Sun’s gravitational force throughout its interior, it’s this nuclear burning that keeps the Sun from either expanding or contracting. The larger your star is, the more radiation is pushing out and the faster you’re burning through your fuel.

And that’s how the Sun works, from the inside out!