This Is Why Scientists Will Never Exactly Solve General Relativity

Even extremely simple configurations in General Relativity cannot be solved exactly. Here’s the science of why.

It’s difficult to appreciate how revolutionary of a transformation it is to consider the Universe from Einstein’s, rather than Newton’s, point of view. According to Newtonian mechanics and Newtonian gravity, the Universe is a perfectly deterministic system. If you were to give a scientist who understood the masses, positions, and momenta of each and every particle in the Universe, they could determine for you where any particle would be and what it would be doing at any point in the future.

In theory, Einstein’s equations are deterministic as well, so you can imagine something similar would occur: if you could only know the mass, position, and momentum of each particle in the Universe, you could compute anything as far into the future as you were willing to look. But whereas you can write down the equations that would govern how these particles would behave in a Newtonian Universe, we can’t practically achieve even that step in a Universe governed by General Relativity. Here’s why.

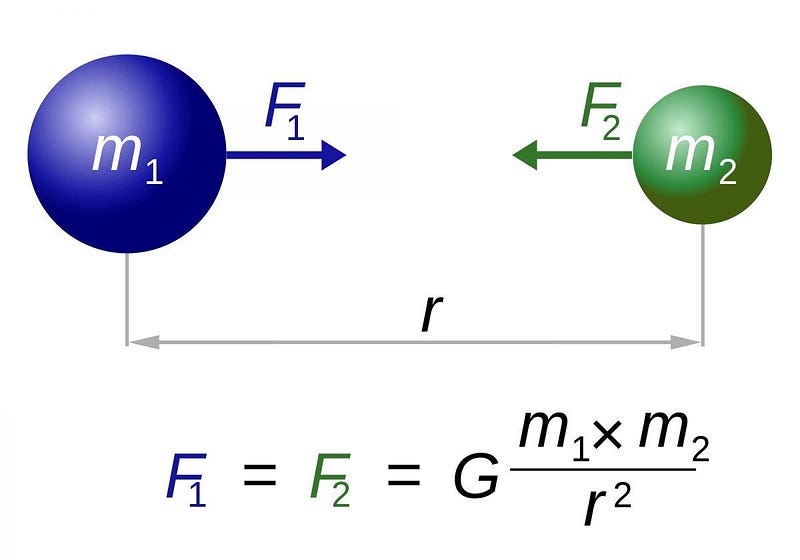
In a Newtonian Universe, every massive object in the Universe exerts a well-defined gravitational force on every other object in the Universe. You can do this so long as you can determine the gravitational force between every pair of masses that exists, and then just calculate the Newtonian gravitational force. That force also tells you how that mass is going to move (because F = ma), and that’s how you can determine the Universe’s evolution.

But in General Relativity, the challenge is much greater. Even if you knew those same pieces of information — positions, masses, and momenta of each particle — plus the particular relativistic reference frame in which they were valid, that wouldn’t be enough to determine how things evolve. The structure of Einstein’s greatest theory is too complex even for that.

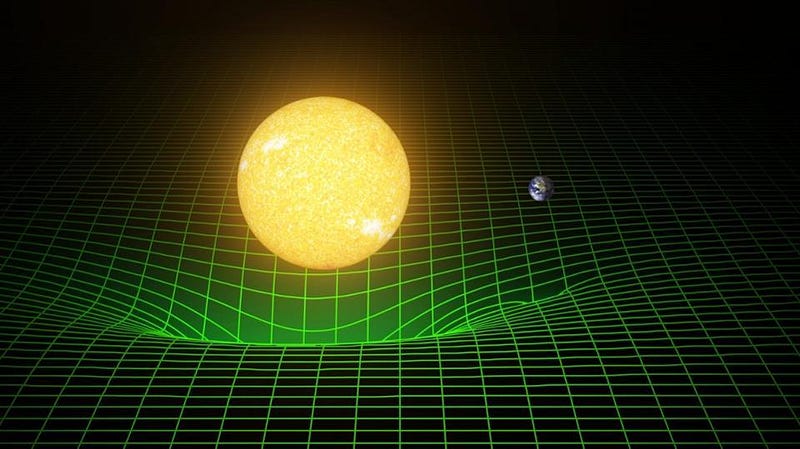
In General Relativity, it isn’t the net force acting on an object that determines how it moves and accelerates, but rather the curvature of space (and spacetime) itself. This immediately poses a problem, because the entity that determines the curvature of space is all of the matter and energy present within the Universe, which includes a lot more than merely the positions and momenta of the massive particles we have.

In General Relativity, unlike Newtonian gravity, the interaction of any mass you consider also plays a role: the fact that it also has energy means that it also deforms the fabric of spacetime. When you have any two massive objects moving and/or accelerating relative to one another in space, it causes the emission of gravitational radiation, too. That radiation isn’t instantaneous, but only propagates outwards at the speed of light. This is an enormously difficult factor to account for.

Whereas you can easily write down the equations that govern any system you can imagine in a Newtonian Universe, even that step is an enormous challenge in a Universe governed by General Relativity. Because of how many things can affect how space itself is curved or otherwise evolves with time, we often cannot even write down the equations that describe the shape of even a simple, toy-model Universe.

Perhaps the most demonstrative example is to imagine the simplest Universe possible: one that was empty, with no matter or energy, and that never changed with time. That’s completely plausible, and is the special case that gives us plain old special relativity and flat, euclidean space. It’s the simplest, most uninteresting case possible.

Now go one step more complex: take a point mass and put it down anywhere in the Universe. All of a sudden, spacetime is tremendously different.

Instead of flat, euclidean space, we find that space is curved, no matter how far away you get from the mass. We find that the closer you get, the faster the space beneath you “flows” towards the location of that point mass. We find that there’s a specific distance at which you’ll cross the event horizon: the point-of-no-return, where you cannot escape even if you were to move arbitrarily close to the speed of light.

This spacetime is much more complicated than empty space, and all we did was add one mass. This was the first exact, non-trivial solution ever discovered in General Relativity: the Schwarzschild solution, which corresponds to a non-rotating black hole.

Over the past century, many other exact solutions have been found, but they’re not significantly more complicated. They include:

• perfect fluid solutions, where the energy, momentum, pressure, and shear stress of the fluid determine your spacetime,
• electrovacuum solutions, where gravitational, electric and magnetic fields can exist (but not masses, electric charges or currents),
• scalar field solutions, including a cosmological constant, dark energy, inflationary spacetimes, and quintessence models,
• solutions with one point mass that rotates (Kerr), has charge (Reissner-Nordstrom), or rotates and has charge (Kerr-Newman),
• or a fluid solution with a point mass (e.g., Schwarzschild-de Sitter space).

You might notice that these solutions are also extraordinarily simple, and don’t include the most basic gravitational system we consider all the time: a Universe where two masses are gravitationally bound together.

This problem — the two-body problem in General Relativity — cannot be solved exactly. There is no exact, analytical solution known for a spacetime with more than one mass in it, and it’s thought (but not, to my knowledge, proven) that no such solution is possible.

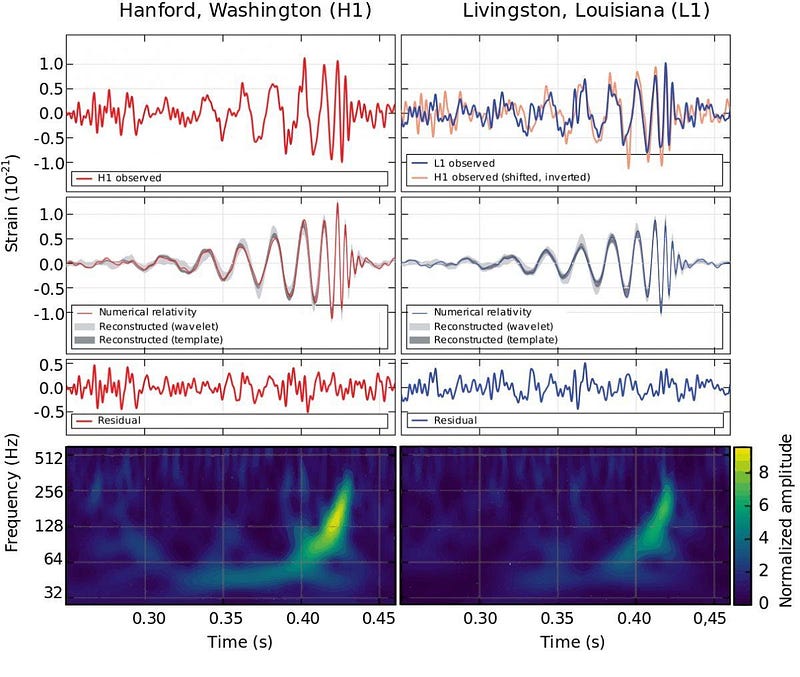
Instead, all we can do is make assumptions and either tease out some higher-order approximate terms (the post-Newtonian expansion) or to examine the specific form of a problem and attempt to solve it numerically. Advances in the science of numerical relativity, particularly in the 1990s and later, are what enabled astrophysicists to calculate and determine templates for a variety of gravitational wave signatures in the Universe, including approximate solutions for two merging black holes. Whenever LIGO or Virgo make a detection, this is the theoretical work that makes it possible.

That said, there are an incredible number of problems we can solve, at least approximately, by taking advantage of the behaviors of solutions that we do understand. We can patch together what happens in an inhomogeneous patch of an otherwise smooth, fluid-filled Universe to learn how overdense regions grow and underdense regions shrink.

We can extract how the behavior of a solvable system differs from Newtonian gravity and then apply those corrections to a more complicated system that perhaps we cannot solve.

Or we can develop novel numerical methods for solving problems that are entirely intractable from a theoretical point of view; so long as the gravitational fields are relatively weak (i.e., we aren’t too close to too large a mass), this is a plausible approach.

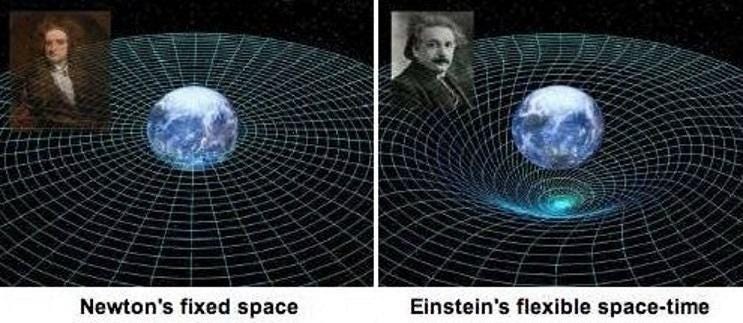
Still, General Relativity poses a unique set of challenges that don’t arise in a Newtonian Universe. The facts are as follows:

• the curvature of space is continuously changing,
• every mass has its own self-energy that also changes spacetime’s curvature,
• objects moving through curved space interact with it and emit gravitational radiation,
• all the gravitational signals generated only move at the speed of light,
• and the object’s velocity relative to any other object results in a relativistic (length contraction and time dilation) transformation that must be accounted for.

When you take all of these into account, it all adds up to most spacetimes that you can imagine, even relatively simple ones, leading to equations that are so complex that we cannot find a solution to Einstein’s equations.

One of the most valuable lessons I ever got in my life came during the first day of my first college math class on differential equations. The professor told us, “Most of the differential equations that exist cannot be solved. And most of the differential equations that can be solved cannot be solved by you.” This is exactly what General Relativity is — a series of coupled differential equations — and the difficulty that it presents to all those who study it.

We cannot even write down the Einstein field equations that describe most spacetimes or most Universes we can imagine. Most of the ones we can write down cannot be solved. And most of the ones that can be solved cannot be solved by me, you, or anyone. But still, we can make approximations that allow us to extract some meaningful predictions and descriptions. In the grand scheme of the cosmos, that’s as close as anyone’s ever gotten to figuring it all out, but there’s still much farther to go. May we never give up until we get there.