All of our “theories of everything” are probably wrong. Here’s why

Our Universe, to the best of our knowledge, doesn’t make sense in an extremely fundamental way. On the one hand, we have quantum physics, which does an exquisite job of describing the fundamental particles and the electromagnetic and nuclear forces and interactions that take place between them. On the other hand, we have General Relativity, which — with equal success — describes the way that matter and energy move through space and time, as well as how space and time themselves evolve in the presence of matter and energy. These two separate ways of viewing the Universe, successful though they may be, simply don’t make sense when you put them together.

When it comes to gravity, we have to treat the Universe classically: all forms of matter-and-energy have well-defined positions and motions through space and time, without uncertainty. But quantum mechanically, position and momentum can’t be simultaneously defined for any quantum of matter or energy; there’s an inherent contradiction between these two ways of viewing the Universe.

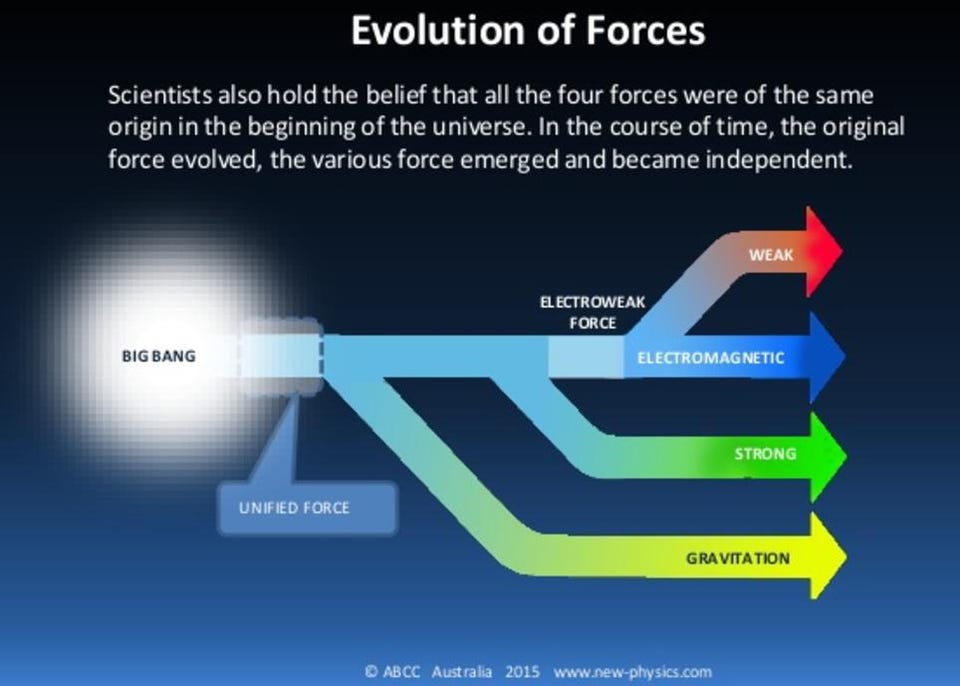
For over 100 years, now, scientists have hoped to find a “theory of everything” that not only resolves this contradiction, but that explains all the forces, interactions, and particles of the Universe with one single, unifying equation. Despite a myriad of attempts at a theory of everything, not a single one has brought us any closer to understanding or explaining our actual reality. Here’s why they’re all quite probably wrong.

An illustration of heavily curved spacetime for a point mass, which corresponds to the physical scenario of being located outside the event horizon of a black hole. If gravity is mediated by a massive force-carrying particle, there will be a departure from Newton’s and Einstein’s laws that are severe at large distances. The fact that we don’t observe that gives us tight constraints on such deviations, but cannot rule out massive gravity.

When General Relativity came along in 1915, the quantum revolution had already begun. Light, described as an electromagnetic wave by Maxwell in the 19th century, had been shown to display particle-like properties as well through the photoelectric effect. Electrons within atoms could only occupy a series of discrete energy levels, demonstrating that nature was often discrete, not always continuous. And scattering experiments showed that, at an elementary level, reality was described by individual quanta, possessing specific properties common to all members of their species.

Nevertheless, Einstein’s General Relativity — which itself had previously unified Special Relativity (motion at all speeds, even close to the speed of light) with gravitation — wove together a four-dimensional fabric of spacetime in order to describe gravity. Building upon it, mathematician Theodor Kaluza, in 1919 took a brilliant but speculative leap: into the fifth dimension.

By adding a fifth spatial dimension to Einstein’s field equations, he could incorporate the classical electromagnetism of Maxwell into the same framework, with the scalar electric potential and the three-vector magnetic potential included as well. This was the first attempt at building a theory of everything: a theory that could describe all the interactions that were happening in the Universe with a single, unifying equation.

In theory, there could be more than three spatial dimensions to our Universe, so long as those “extra” dimensions are below a certain critical size that our experiments have already probed. There is a range of sizes in between ~10^-19 and 10^-35 meters that are still allowed for a fourth (or more) spatial dimension, but nothing that physically occurs in the Universe can be allowed to rely on that fifth dimension.

But there were three problems of Kaluza’s theory that posed difficulties.

1. There was absolutely no dependence of anything that we observed in our four-dimensional spacetime on the fifth dimension itself; it must somehow “disappear” from all of the equations that impacted physical observables.
2. The Universe isn’t simply made of classical (Maxwell’s) electromagnetism and classical (Einstein’s) gravity, but exhibited phenomena that couldn’t be explained by either, such as radioactive decay and quantization of energy.
3. And Kaluza’s theory also included an “extra” field: the dilaton, that played no role in either Maxwell’s electromagnetism or Einstein’s gravity. Somehow, that field has to disappear as well.

When people refer to Einstein’s pursuit of a unified theory, they often wonder, “Why did everyone abandon what Einstein was working on after his death?” And these problems are part of the reason why: Einstein never updated his pursuits to include our knowledge of the quantum Universe. As soon as we learned that it wasn’t just particles that had quantum properties, but quantum fields too — i.e., the invisible interactions that permeated even empty space were quantum in nature — it became obvious that any purely classical attempt to build a theory of everything would necessarily omit an obvious necessity: the full scope of the quantum realm.

Parity, or mirror-symmetry, is one of the three fundamental symmetries in the Universe, along with time-reversal and charge-conjugation symmetry. If particles spin in one direction and decay along a particular axis, then flipping them in the mirror should mean they can spin in the opposite direction and decay along the same axis. This was observed not to be the case for the weak decays, which are the only interactions known to violate charge-conjugation (C) symmetry, parity (P) symmetry, and the combination (CP) of those two symmetries as well.

However, another potential path to a theory of everything was beginning to unveil itself instead during the middle of the 20th century: the notion of symmetries and symmetry-breaking in quantum field theories. Here in our modern, low-energy Universe, there are many important ways that nature is not symmetric.

• Neutrinos are always left-handed and antineutrinos are always right-handed, and never the other way around.
• We inhabit a Universe that’s almost exclusively made of matter and not antimatter, but where all reactions we know to create only create or destroy equal amounts of matter and antimatter.
• And some interactions — most notably, particles interacting through the weak force — exhibit asymmetries when particles are replaced with antiparticles, when reflected in a mirror, or when their clocks are run backward instead of forward.

However, at least one symmetry that’s badly broken today, the electroweak symmetry, was restored at earlier times and higher energies. The theory of electroweak unification was vindicated with the subsequent discovery of the massive W-and-Z bosons, and later, the entire mechanism was validated with the discovery of the Higgs boson.

It makes one wonder: if the electromagnetic and weak forces unify under some early, high-energy conditions, could the strong nuclear force and even gravity join them at an even higher scale?

The idea of unification holds that all three of the Standard Model forces, and perhaps even gravity at higher energies, are unified together in a single framework. This idea, although it remains popular and mathematically compelling, does not have any direct evidence in support of its relevance to reality.

This wasn’t some obscure idea that took a brilliant insight to arrive at, but rather a path that a great number of mainstream physicists followed: the path of grand unification. Each of the three known quantum forces could be described by a Lie group from the mathematics of group theory.

• The SU(3) group describes the strong nuclear force, which holds protons and neutrons together.
• The SU(2) group describes the weak nuclear force, responsible for radioactive decays and the flavor changes of all quarks and leptons.
• And the U(1) group describes the electromagnetic force, responsible for electric charge, currents, and light.

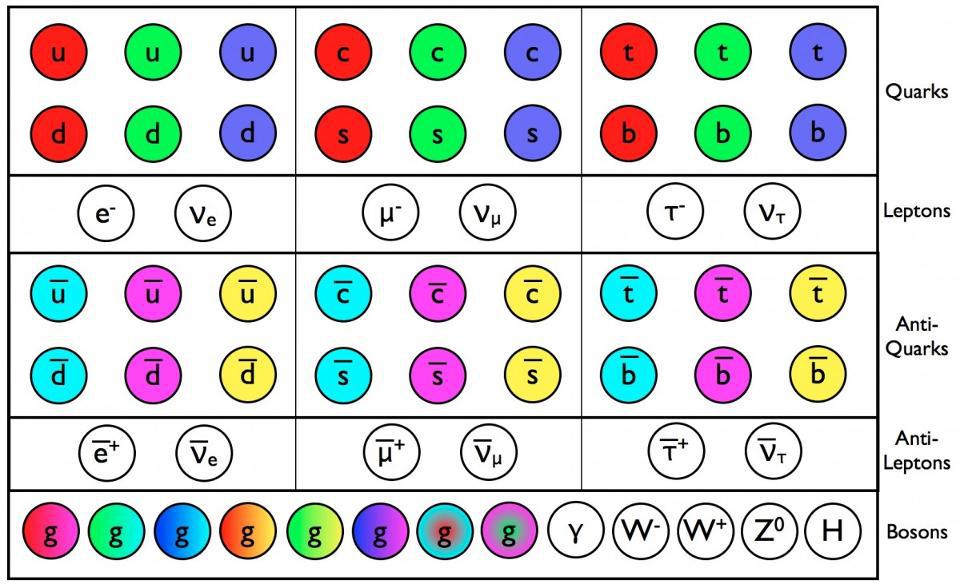
The full Standard Model, then, can be expressed as SU(3) ⊗ SU(2) ⊗ U(1), but not in the way you might think. You might think, seeing this, that SU(3) = “the strong force,” SU(2) = “the weak force,” and U(1) = “the electromagnetic force,” but this is not true. The problem with this interpretation is that we know that the electromagnetic and the weak components of the Standard Model overlap, and cannot be separated out cleanly. Therefore, the U(1) part isn’t purely electromagnetic, and the SU(2) part isn’t purely weak; there has to be mixing in there. It’s more accurate to say that SU(3) = “the strong force” and that SU(2) ⊗ U(1) = “the electroweak part,” and that’s why the discovery of the W-and-Z bosons, plus the Higgs boson, were so important.

The group structure of the Standard Model, SU(3) x SU(2) x U(1), can be embedded in a number of larger groups, including SU(5) and SO(10). In terms of Dynkin diagrams, you must “erase” one dot to get the Standard Model back from SU(5), and two dots, in whatever your preferred order is, to get it back from SO(10). SO(10) also contains SU(5), and both contain numerous particles for which there is no evidence in our particle physics experiments.

It seems like an easy extension, logically, that if these groups, combined, describe the Standard Model and the forces/interactions that exist in our low-energy Universe, perhaps there’s some larger group that not only contains them all, but that under some set of high-energy conditions, represents a unified “strong-electroweak” force. This was the original idea behind Grand Unified Theories, which would either:

• restore a left-right symmetry to nature, rather than the chiral asymmetry found in the Standard Model,
• or, much like Kaluza’s original attempt at unification, necessitate the existence of new particles: the superheavy X-and-Y bosons, which couple to both quarks and leptons and demand that the proton be a fundamentally unstable particle,
• or demand both: a left-right symmetry and these superheavy particles, plus perhaps even more.

However, no matter what experiments we’ve performed under any arbitrary conditions — including the highest-energy ones seen in LHC data and from cosmic ray interactions — the Universe still remains fundamentally asymmetric between left-handed and right-handed particles, these new particles are nowhere to be found, and the proton never decays, with its lifetime having been established to be upward of ~10³⁴ years. That last limit, already is a factor of ~10,000 more stringent than Georgi-Glashow SU(5) unification allows.

The particle content of the hypothetical grand unified group SU(5), which contains the entirety of the Standard Model plus additional particles. In particular, there are a series of (necessarily superheavy) bosons, labeled “X” in this diagram, that contain both properties of quarks and leptons, together, and would cause the proton to be fundamentally unstable. Their absence, and the proton’s observed stability, provide strong evidence against the validity of this theory in a scientific sense.

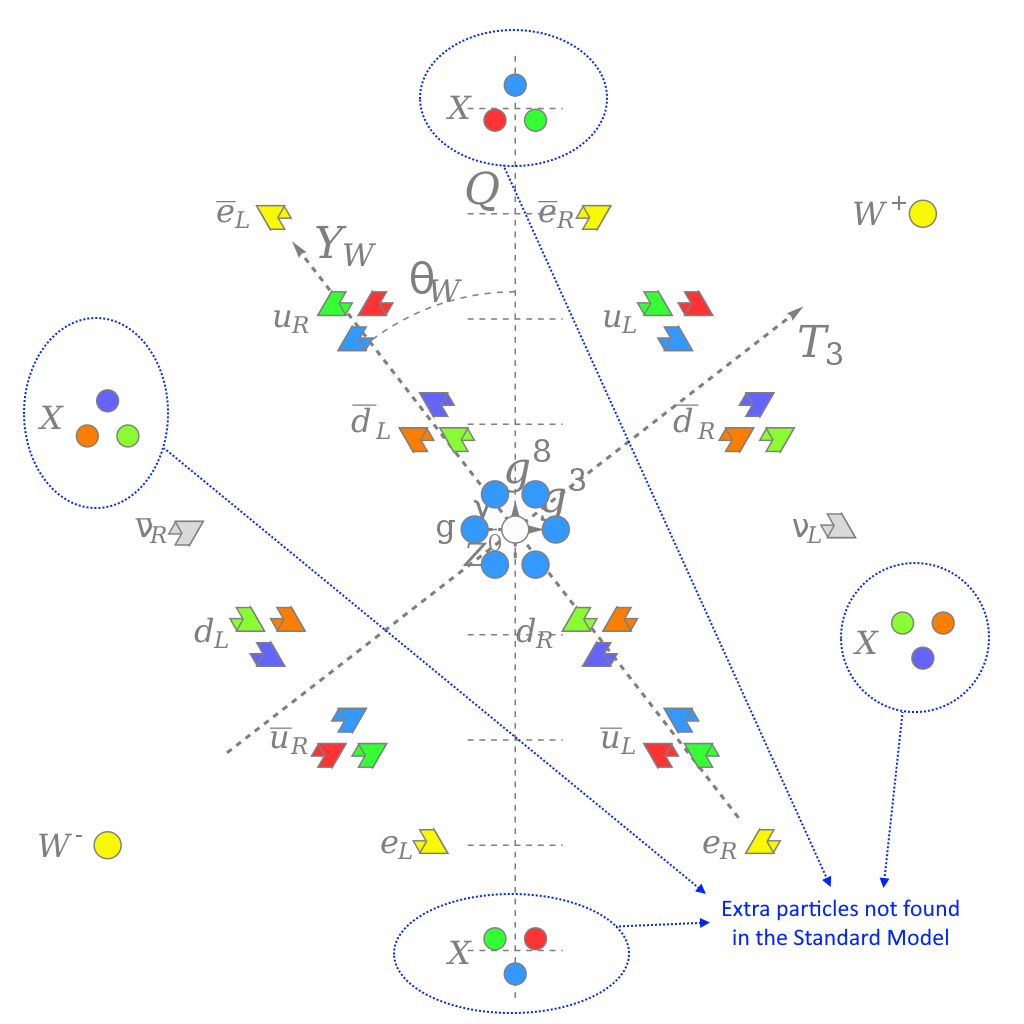
This is a suggestive line of thought, but when you follow it through to its conclusion, the new particles and phenomena that are predicted simply don’t materialize in our Universe. Either something is suppressing them, or perhaps these particles and phenomena aren’t a part of our reality.

Another approach that was tried was to examine the three quantum forces within our Universe, and to take a specific look at the strength of their interactions. While the strong nuclear, weak nuclear, and electromagnetic forces all have different interaction strengths today, at everyday (low) energies, it’s been known for a long time that the strengths of these forces change as we probe higher and higher energies.

At higher energies, the strong force gets weaker, while the electromagnetic and weak forces both get stronger, with the electromagnetic force getting stronger more rapidly than the weak force as we go to successively higher energies. If we only include the particles of the Standard Model, the interaction strength of these forces almost meets at a single point, but not quite; they miss by just a little bit. However, if we add new particles into the theory — which should arise in a number of extensions to the Standard Model, such as supersymmetry — then the coupling constants change differently, and might even meet, overlapping at some very high energy.

The running of the three fundamental coupling constants (electromagnetic, weak, and strong) with energy, in the Standard Model (left) and with a new set of supersymmetric particles (right) included. The fact that the three lines almost meet is a suggestion that they might meet if new particles or interactions are found beyond the Standard Model, but the running of these constants is perfectly within expectations of the Standard Model alone. The fact that the coupling constants may all meet at a point in supersymmetric (SUSY) scenarios may not mean very much for reality.

But this is a challenging game to play, and it’s easy to see why. The more you want things to “come together” in some way at high energies, the more new things you need to introduce into your theory. But the more new things you introduce into your theory, such as:

• new particles,
• new forces,
• new interactions,
• or new dimensions,

the more and more difficult it becomes to hide the effects of their presence, even in our modern, low-energy Universe.

For example, if you favor string theory, a “small” unification group like SU(5) or SO(10) are woefully inadequate. To ensure left-right symmetry — i.e., that particles, which are excitations of the string field, can move both counterclockwise (leftward) and clockwise (rightward) — you need to have bosonic strings move in 26 dimensions and superstrings moving in 10 dimensions. In order to have both, you need a mathematical space with a particular set of properties that accounts for the 16-dimensional mismatch. The only two known groups with the right properties are SO(32) and E₈ ⊗ E₈, which both require an enormous number of new “additions” to the theory.

The difference between a Lie algebra based on the E(8) group (left) and the Standard Model (right). The Lie algebra that defines the Standard Model is mathematically a 12-dimensional entity; the E(8) group is fundamentally a 248-dimensional entity. There is a lot that has to go away to get back the Standard Model from string theories as we know them; with fewer parameters and fewer assumptions, our presently understood Universe is much more simply described by the Standard Model and general relativity than any other description.

It’s true that string theory does offer a hope for a single theory of everything in one sense: these enormous superstructures that describe them, mathematically, do in fact contain all of General Relativity and all of the Standard Model within them.

That’s good!

But they also contain much, much more than that. General Relativity is a tensor theory of gravity in four dimensions: matter and energy deform the fabric of spacetime (with three space dimensions and one time dimension) in a very particular way, and then move through that distorted spacetime. In particular, there are no “scalar” or “vector” components to it, and yet, what’s contained within string theory is a ten dimensional scalar-tensor theory of gravity. Somehow six of those dimensions, as well as the “scalar” part of the theory, must all go away.

In addition, string theory also contains the Standard Model with its six quarks and antiquarks, six leptons and antileptons, and the bosons: gluons, W-and-Z bosons, the photon, and the Higgs boson. But it also contains several hundred new particles: all of which must be “hidden away” somewhere in our present Universe.

The string landscape might be a fascinating idea that’s full of theoretical potential, but it cannot explain why the value of such a finely-tuned parameter like the cosmological constant, the initial expansion rate, or the total energy density have the values that they do. Each “pocket” of the string landscape has its own unique vacuum expectation value, which corresponds to a value for a fundamental constant in the Universe.

It’s for this reason that searching for a “theory of everything” is a very difficult game to play: almost any modification you can make to our current theories is either highly constrained or already ruled out by existing data. Most of the other alternatives touting to be “theories of everything,” including:

• Erik Verlinde’s entropic gravity,
• Stephen Wolfram’s “new kind of science,”
• or Eric Weinstein’s Geometric Unity,

all suffer from not only these problems, they struggle mightily to even recover and reproduce what’s already known and established by present-day science.

All of which isn’t to say that searching for a “theory of everything” is necessarily wrong or impossible, but that it’s an incredibly tall order that no theory that presently exists has accomplished. Remember, in any scientific endeavor, if you want to replace the currently prevailing scientific theory in any realm, you must meet all three of these critical steps:

1. Reproduce all of the successes and victories of the present theory.
2. Explain certain puzzles that the present theory cannot explain.
3. And make new predictions that differ from the present theory, that we can then go out and test.

To date, even “step 1” can only be claimed if certain new puzzles that rear their heads in purported theories of everything are swept under the rug, and almost all such theories either fail to make a novel prediction or are already dead-in-the-water because what they predicted hasn’t panned out. It’s true that theorists are free to spend their lives on whatever endeavors they choose, but if you’re questing for a theory of everything, beware: the goal that you seek may not even exist in nature.