The Scientific Failure Of The Original Elegant Universe
Elegance, beauty, and mathematical precision makes for a compelling story and an exquisite model. But it doesn’t make it right.
Scientific theories, at their best, are simple, straightforward, full of predictive power, and contain an elegance or beauty all their own. Newton’s simple F = ma and Einstein’s E = mc² are simple equations that house profound truths and enable so much to be derived; the quark model and General Relativity are simple to describe but incredibly deep theories that govern the interactions of particles; ideas like supersymmetry, grand unification and string theory extend the known physical symmetries to even greater levels. Many physicists think the way to new, profound truths about existence is through more symmetries and greater elegance. By applying new avenues of mathematics to the Universe, we seek a deeper truth to reality than our current understanding. But the original “elegant Universe” model, Kepler’s Mysterium Cosmographicum, was symmetric, beautiful, and based in never-before-applied mathematics. In a great cautionary tale, it was also an enormous scientific failure.
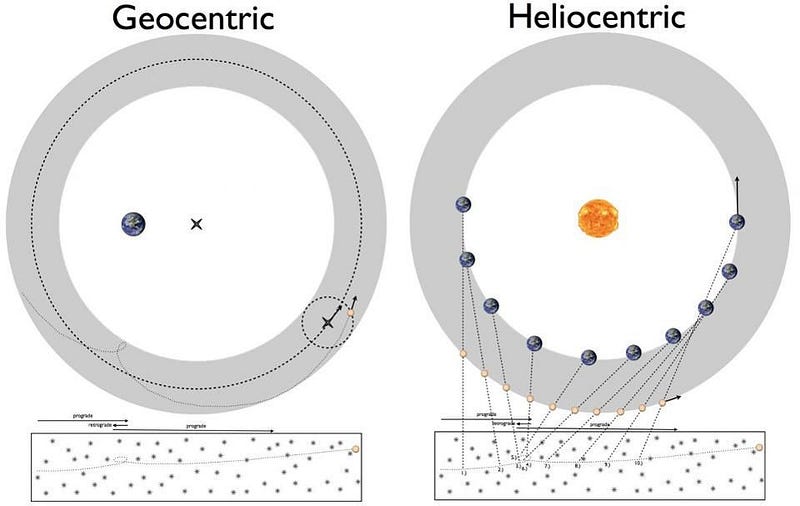
Prior to Kepler, there were three major systems describing the Universe:
- The Ptolemaic model, where the Earth was stationary, and everything orbited the Earth in a series of circles, using the math of equants, deferents, and epicycles.
- The Copernican model, where the Sun was stationary, and Earth was just one of six planets that orbited the Sun in a circular fashion, also using epicycles.
- The Tychonian model, where the Sun orbited the Earth and then all the other planets orbited the Sun, all in circles, all using epicycles.
Writing decades before Galileo rose to prominence, Kepler thought that the heliocentric ideas had promise, but they needed something more than just circles. They needed an elegant mathematical structure to support them. In a stroke of brilliance, at just 24 years of age, Kepler published what he thought was the most beautiful idea he ever had.
With six planets to orbit the Sun (none beyond Saturn would be discovered until nearly 200 years later), Kepler recognized that there must be six unique orbits: one for each of the planets. But why six? Why not more; why not fewer? And why did they have the spacings that we observed? The connection between these orbits and mathematics was his idea for the elegant Universe:
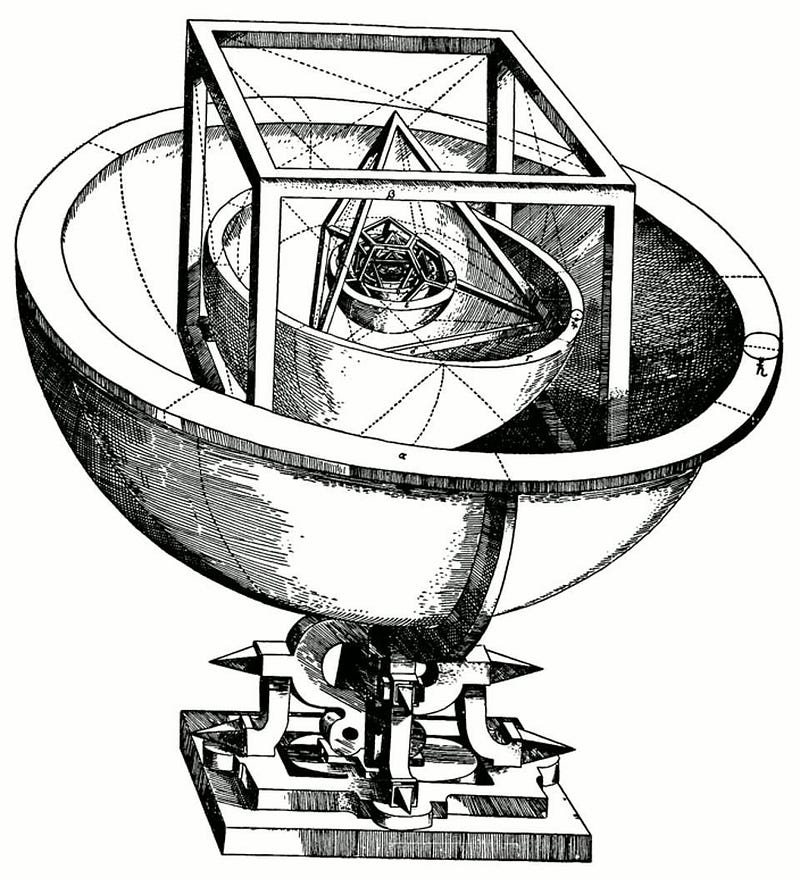
I propose to show that God, in creating the universe and arranging the spheres, had in view the five regular solids of geometry, and fixed by their dimensions the number, proportions and motions of the spheres.
You see, in three dimensions, there are exactly five solids that you can build out of regular polygons: no more, no less. Discovered by the ancient Greeks over 2,000 years prior and known as the five Platonic solids (though they predate Plato substantially), Kepler envisioned a series of nested spheres, circumscribed and inscribed around each of the five solids, resulting in six spherical orbits for the planets to move along.
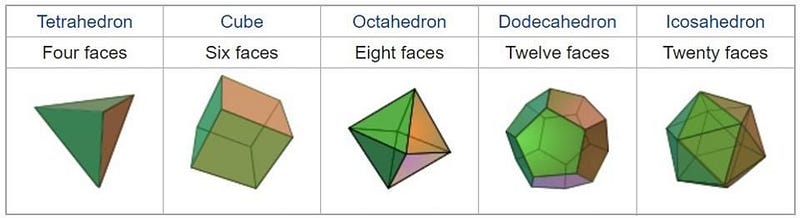
The sphere of Mercury would be the innermost one, inscribed within an octahedron, the regular polygon made up of eight equilateral triangles. Circumscribed around that is the sphere holding Venus, which itself is inscribed within an icosahedron, a 20-sided polygon made of equilateral triangles. Around that is Earth’s sphere, which is inscribed within a dodecahedron, which has 12 sides each made out of a pentagon. Circumscribing the dodecahedron is the sphere of Mars, which then itself is inscribed within the tetrahedron: a four-sided polygon where each side is an equilateral triangle. Around the tetrahedron is the sphere of Jupiter, which is inscribed within a cube: the final solid. At last, enclosing the cube is one final sphere, where the planet Saturn orbits.

Kepler’s idea was nothing short of brilliant, and each of the ratios for the planetary radii were predicted exactly by his model. The problem came when you compared them with observations. While the ratios for Mercury to Venus, Venus to Earth, and Earth to Mars lined up pretty well, the final two worlds failed to adhere to Kepler’s predicted ratios. In particular, it orbit of Mars, and its failure to conform to a circle of any type, was the downfall of Kepler’s model. Even though Kepler continued to work on it, even publishing a second edition more than 20 years later, his most remarkable contribution came from doing what most scientists can never bring themselves to do: abandoning their most cherished hypothesis.

NASA / JPL
The orbits of the planets in the inner solar system aren’t exactly circular, but they’re quite close, with Mercury and Mars having the biggest departures and the greatest ellipticities. Additionally, objects like comets and asteroids make ellipses as well and obey the rest of Kepler’s laws, so long as they’re bound to the Sun.
It wasn’t nested spheres that predicted planetary motion correctly, but ellipses. Kepler’s three laws, that planets move in ellipses around the Sun, that they sweep out equal areas in equal times, and that the ratio of the squares of the orbital period to the cube of the semimajor axis are a constant for any central mass, both contradicted and superseded his Mysterium Cosmographicum. The success of his elliptical orbits paved the way for Newton’s law of universal gravitation, and ushered in the science of astrophysics. Despite his undying love for his most brilliant idea, it was the less elegant model that better described our Universe. By leaving aside his own hopes and instead letting the data be his guide, he was able to make the advance that a lesser mind would have failed to discover.
There is a temptation towards reductionism in physics: to describe as much as possible with as little as possible. The idea that there exists a theory of everything, or a single theory that can predict and describe everything that can be predicted or described in the Universe to the maximum possible accuracy, is the ultimate dream of a great many scientists. Yet there is no guarantee, even in principle, that it’s possible for such a dream to come true. As famed physicist Lincoln Wolfenstein put it:
The lesson from Kepler is not that we must refrain from asking what seem to be fundamental questions; the lesson is that we cannot know whether there is any simple answer or where it may come from.
Elegance, beauty, and reductionism may offer some tremendous opportunities for successfully predicting new physical phenomena, but there’s no guarantee these predictions will be borne out in reality. When it comes to uncovering the next great breakthrough in fundamental science, our hopes and dreams that we’ll be closer to a unified theory of everything through mathematical beauty and additional symmetry is a common one, but is no sure thing. May we all be as open to whatever the data tells us as Kepler was, and be willing to follow it, no matter where it leads.
Ethan Siegel is the author of Beyond the Galaxy and Treknology. You can pre-order his third book, currently in development: the Encyclopaedia Cosmologica.