The Biggest Fundamental Questions That ‘42’ Really Is The Answer To

We’re still not sure what the ultimate question is. Here are 5 excellent candidates.
One of the most amusing stories in all of science fiction is Douglas Adams’ The Hitchhiker’s Guide to the Galaxy, where a supercomputer is tasked with uncovering “the answer.” Allegedly designed to give the answer to the ultimate question about life, the Universe, and everything, the computer spends 7.5 million years calculating what the answer would be, and finally spits it out: 42. Only, when the answer is finally revealed, no one can remember what “the ultimate question” actually was.
Fortunately, there are a number of fundamental questions in both math and physics that do have 42 as their answer. Could any of them have passed for the ultimate question about life, the Universe, and everything? Although no one can be sure — even in this fictional world — these five possibilities are among the most fascinating. Here are five fascination questions for which 42 truly is the correct answer.

1.) At how many degrees, offset from the Sun (or any light source), is a rainbow produced? There are many ways to create a rainbow: from raindrops to waterfalls to garden hoses to mist to the spray from bodies of water. Yet all of them have a few things in common. They all arise from light reflecting off of water droplets. They all originate in a direction that opposes the direction of a light source. And they all — so long as they’re created from droplets of fresh water — have a peak intensity that’s in an arc-like shape that’s offset 42° from the direction of the light source.
Every primary rainbow you’ve ever seen displays the same angle-of-arc. If there’s a rainbow that the Sun is creating, looking exactly opposite to the direction of the Sun and look for a circle (or portion of a circle) that’s offset from that direction by 42° will enable you to see it. The reason is simple physics: light behaves as a ray, the speed of light in water is different than the speed of light in air, and when light enters or leaves that medium, it always bends in a predictable way determined by the angle-of-incidence at the interface between the water and the air.
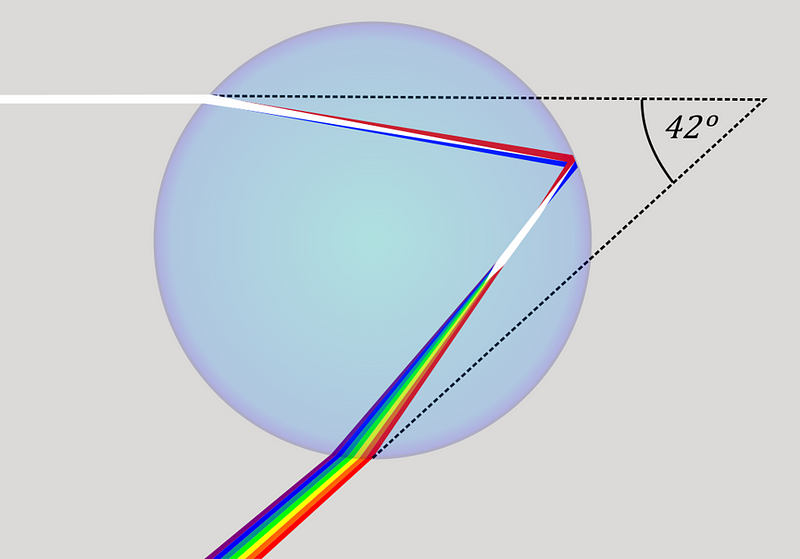
When light moves from air into water, different wavelengths bend at slightly different angles, causing the colors to disperse. When light strikes the back of the water droplet (and it’s a very good assumption that all droplets are perfectly spherical), it reflects at a known, predictable angle. And when it re-emerges back into the air, each wavelength moves off at a specific angle-of-offset from the original: from just under 41° to a little under 43° over the visible light spectrum, with the peak intensity occurring at 42°.
Any planet with a thin atmosphere, transparent to visible light, where light travels close to the speed of light in a vacuum and where pure water droplets exist in the atmosphere will see that same 42° rainbow phenomenon. However, it’s not truly universal: if the atmosphere has a non-negligible index of refraction, if droplets are elliptical instead of spherical, if they’re made of saltwater instead of freshwater, or if they’re made of a different substance entirely, the rainbow can occur at an entirely different angle.
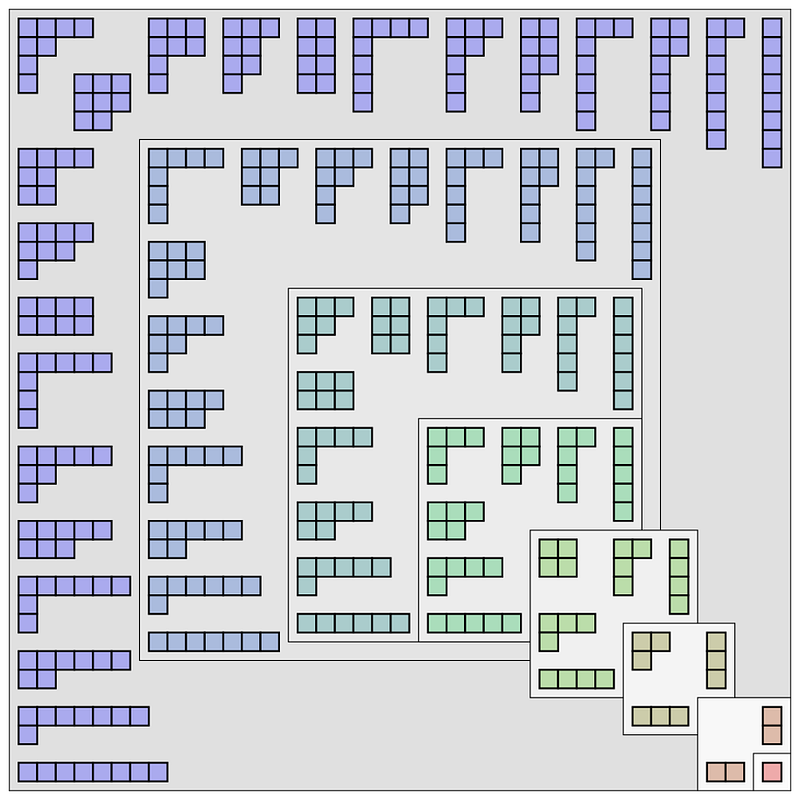
2.) What is the number of ways that you can partition the number 10? In mathematics, partitioning has a very special meaning: how many unique ways can you add up positive integers to create a certain number? For example, there are 7 ways to partition the number 5:
- 1 + 1 + 1 + 1 + 1,
- 1 + 1 + 1 + 2,
- 1 + 1 + 3,
- 1 + 2 + 2,
- 1 + 4,
- 2 + 3,
- 5.
For the number 10, with all the different ways to do it, there are a total of 42 unique ways to do it. Fascinatingly, this isn’t the only relationship between 10 and 42, as 10 can be written as 2¹ + 2³, while 42 can be written as 2¹ + 2³ + 2⁵. If we were to write these numbers in binary, “10” would become 1010, while “42” would become 101010. These numbers and these relationships play important roles in both mathematics and physics (particularly through group theory), with 42 having some fascinating properties completely independent of any measured physical phenomena.
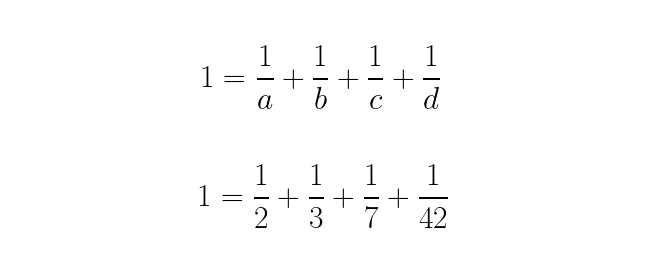
3.) What is the largest integer whose reciprocal, along with three other unique integer reciprocals, adds up to 1? Here’s a math puzzle for you: can you find four positive integers, like a, b, c, and d, where (1/a) + (1/b) + (1/c) + (1/d) = 1? It’s easy to do if you make certain choices. For example, if a, b, c, and d all equal 4, this is very simple. If you even allow two of these numbers to be equal, there are many possible solutions: a=2, b=4, and c=d=8; a=b=3, c=4, d=12; etc.
But if you insist that all four of these numbers must be different from one another, there are very few unique solutions. And the largest number that you can use to try and satisfy this equation that still gives you a solution? 42. If you let a=2, b=3, and c=7, then d=42 and the equation works. Interestingly enough, that’s not the only relationship between those four numbers, as 2, 3, and 7 are the prime factors of 42: 42 = 2 × 3 × 7. In even a purely mathematical sense, 42 has some fascinating properties.
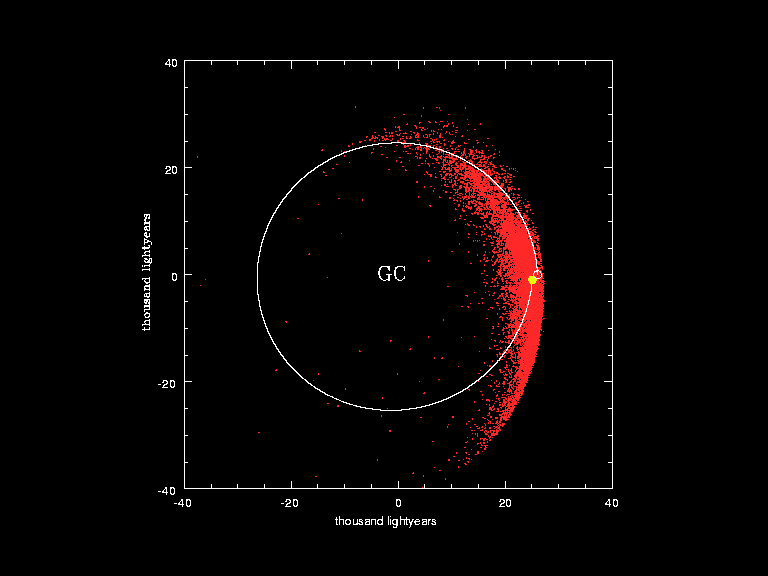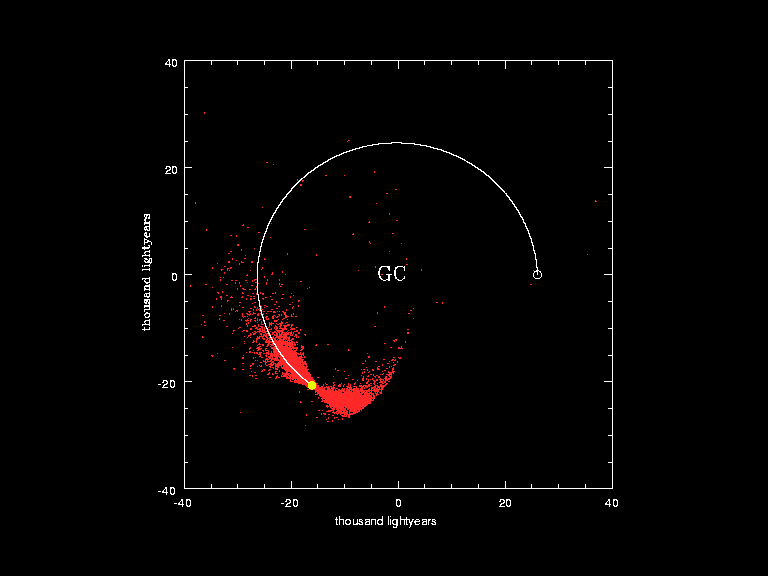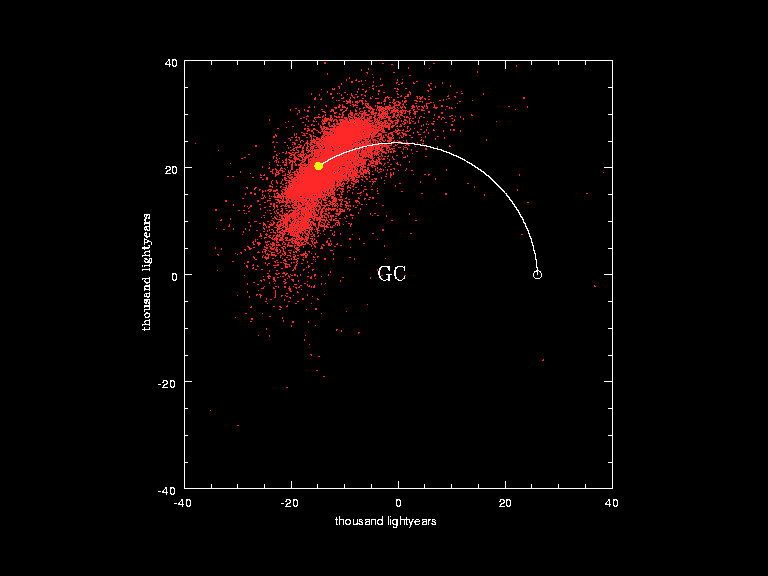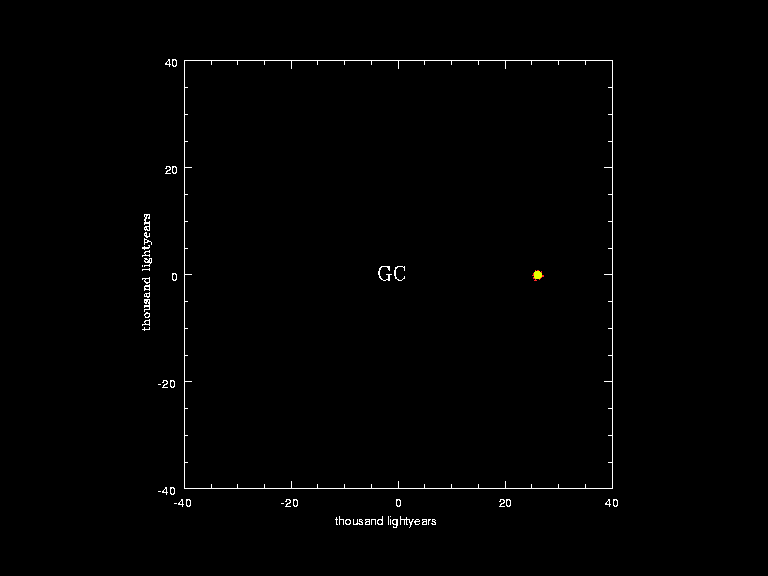
4.) How many times will the Sun orbit the Milky Way before catastrophically transforming into a red giant? This is one of the most fun facts about our Solar System, where the planets revolve around the Sun and the Sun revolves around center of the Milky Way. There’s only a finite amount of time that the Sun will live, with various milestones marking its critical transitions. It takes tens of millions of years for the proto-stellar nebula that gives rise to our Solar System to form our Sun, which officially becomes a star once nuclear fusion of hydrogen into helium ignites in its core.
After that, the Sun will chug along for billions of years until the core runs out of hydrogen fuel, at which point it will begin to swell into a red giant, burning hydrogen in a shell until the helium core ignites. During this phase, Mercury and Venus will certainly be engulfed, and it’s likely (but not certain) that the Earth will be swallowed as well. Icy worlds, like Triton, Pluto, and most of the Kuiper belt objects, will boil away almost entirely. This giant phase lasts for hundreds of millions of years while helium burns to completion. At that point, the Sun will blow off its outer layers, dying in a planetary nebula/white dwarf combination.

Yet, throughout all of these changes, the Sun and our Solar System will continue to orbit around the Milky Way’s center, completing a full orbit every ~250 million years or so. The time to return to our starting point is known as a galactic year, and has about a ~10% uncertainty on how long it actually takes. Meanwhile, in term of stellar evolution, we are quite confident that the Sun will last roughly 10–12 billion years from the moment nuclear fusion first ignites in its core until the red giant phase begins.
So, how many galactic years will the Sun (and Earth) experience before the Sun swells into a red giant and planet Earth is (likely) completely destroyed?
42.
Although justifiable estimates typically range from about 40 to 45 — driven largely by the uncertainty in how fast the Sun is orbiting around the Milky Way’s center — 42 is an answer that’s extremely consistent with the best data we have. It may yet turn out to be the exact answer to this question, although superior data will be required to know for certain.

5.) How fast is the Universe expanding today? Right now, we exist in the Universe precisely 13.8 billion years after the earliest stages of the hot Big Bang occurred. For all of cosmic time, the Universe has been expanding and cooling, and that means it’s been getting less dense. In the expanding Universe, the thing that determines your expansion rate is the density of all the different forms of energy combined, so an expanding Universe filled with matter and radiation will have the expansion inevitably slow down over time.
The expansion rate, today, is slower than it’s ever been at any time in the past, and continues to gradually slow down. If we wait for a long enough time, the matter and radiation density will drop to zero, with only dark energy — the energy inherent to space itself — remaining. By convention (and for no other reason), we typically report the expansion rate as a speed (how fast something appears to be moving) per unit distance (based on how far away it is from us): in units of kilometers-per-second, per megaparsec.
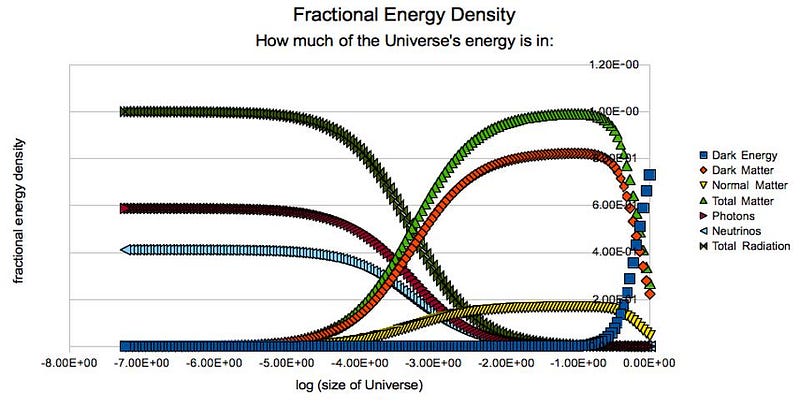
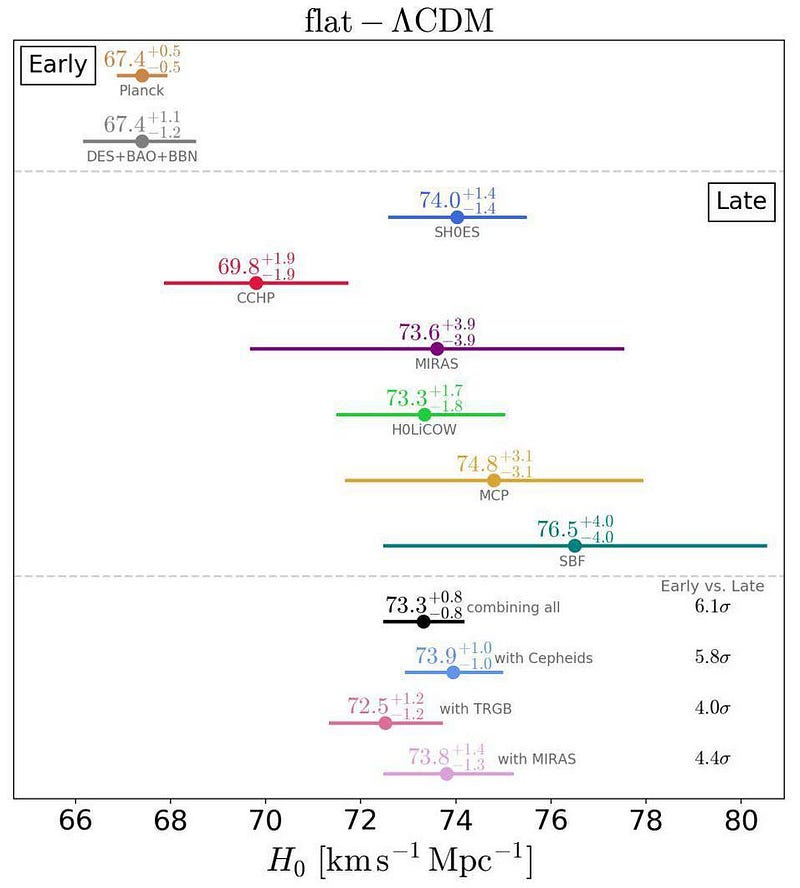
In those units, we have two classes of measurements that point to inconsistent values: measurements that are based on relics imprinted from early times, like fluctuations in the cosmic microwave background or galaxy clustering in the large-scale structure, and measurements that come from individual sources at late cosmic times, like supernovae or gravitational lenses. The first set of measurements yields a value of 67–68 km/s/Mpc, while the second yields a value of 73–74 km/s/Mpc. Figuring out what the resolution to this puzzle is — i.e., which group is correct, and why — is one of modern cosmology’s biggest challenges.
But if the first group is right, then perhaps the answer to the question of how fast the Universe is expanding really is 42. Not in kilometers-per-second-per-megaparsec, but if we used miles instead of kilometers. Doing that conversion, from kilometers into miles, transforms the first value of the expansion rate into 42 mi/s/Mpc, which could easily be construed as the answer to the biggest question in entire cosmos: how fast is the Universe expanding right now? Although more science will be required to solve this cosmic conundrum, “42” is well within the realm of possible, or even probable, answers.
All told, there are many questions that 42 is clearly the answer to, but only a few of those questions have fundamental, universal, or cosmic implications. If it truly is the answer to the ultimate question about life, the Universe, and everything, we owe it to ourselves to try and reconstruct just what that question might be. From mathematics to physics, five vital questions emerge that legitimately have 42 as their answer.
Rainbows always emerge offset at an angle of 42° relative to the light source that creates them.
The number 10 can be mathematically partitioned exactly 42 different ways.
42 is the largest number whose reciprocal, added with three other unique positive integers, sums to exactly 1.
42 is the number of galactic years that the Sun-Earth system will survive before it’s destroyed.
And 42 is the expansion rate of the entire Universe, in miles-per-second-per-megaparsec.
It really could be the answer to the ultimate question about life, the Universe, and everything. Now, we just have to figure out what that question actually is!
Starts With A Bang is written by Ethan Siegel, Ph.D., author of Beyond The Galaxy, and Treknology: The Science of Star Trek from Tricorders to Warp Drive.





