Ask Ethan: How do telescopes look back in time?
- You'll often see claims that telescopes are seeing galaxies as they were a specific amount of time in the past, and that the Big Bang occurred precisely 13.8 billion years ago.
- But one of the key lessons from Einstein's theory of relativity is that neither time nor space are absolute, but that every individual observer measures them uniquely.
- So how then, do we establish a notion of how far back in time we're looking when we see an object or phenomenon from far away in the distant Universe? It's a fascinating puzzle to solve.
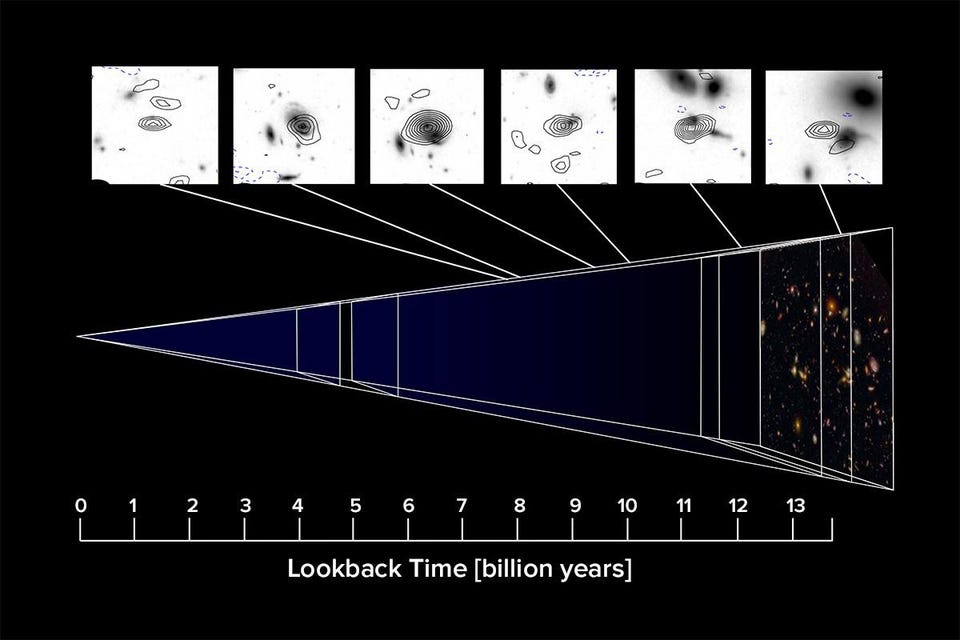
Whenever we observe anything in the Universe, we’re not seeing it as it is right now, at this exact moment we’re experiencing. Instead, we see it as it was a specific amount of time ago, as it takes a finite amount of time for the emitted signal to reach us and be both recorded and processed by either our senses or our equipment. For most signals that happen here on Earth, especially those that occur very close to us, this delay is negligible, and it’s an excellent approximation to ignore those minuscule differences. But for signals originating from the depths of space, the great cosmic distances between objects start to matter tremendously.
Is it too simple and naïve, then, to simply determine how far away an object is and use the known value of the speed of light to determine how “long ago” we’re seeing such an object? And what would Einstein have to say about all of this, anyway? That’s what Robert Allen wants to know, writing in to ask:
“What does it mean when astronomers say that telescopes such as [JWST] are seeing those galaxies ‘as they were billions of years ago?’ How can we even talk about the state of distant galaxies ‘now’ or ’10 billion years ago’ when special relativity prohibits establishing a temporal equivalence between inertial reference frames?”
It’s not a very easy question to answer, but it’s important to tackle it head on. Here’s what we know.

Prior to Einstein, there was this notion that space and time were absolute: they existed universally for every possible observer. No matter where you were, when you were, or how you were moving through the Universe, it was assumed that your notions of what “space” and “time” were would agree with everyone else’s.
We now know that cannot be true, for one simple reason: everyone, everywhere, and everywhen always agrees that the speed of light in a vacuum, c, is the same universal constant: 299,792,458 m/s.
Imagine that there are two identical copies of you, and you shine a light-emitting source like a flashlight in whatever direction you decide is “forward.” Now, imagine one copy of you remains stationary, while the other copy chases after the light as fast as they can. If time passed at the same rate for both of you, the copy that “chased the light” would observe a slower speed of light than the stationary copy! The only way to make sense of this, with a constant speed of light, is if time passes at a slower rate for the light-chasing observer than the stationary one, and if your perception of time changes, then your perception of space must change too: hence the concepts of time dilation and length contraction.

Things get even more intricate when we introduce gravitation into the picture. Instead of simply needing to adjust our notions of time and space for observers in relative motion and in different locations to one another, we also have to acknowledge the fact that spacetime itself isn’t a flat, constant entity, even in the absence of observers. Features that need to be taken into account include:
- the effects of massive objects, which cause time to dilate, space to curve, and light to redshift/blueshift (among other effects) dependent on how close or far away they are from the mass in question,
- the effects of the expanding Universe, which change the amount of space that light must travel through on its journey from the emitting source to the observing destination, as well as stretching the wavelength of light along its journey,
- and the effects arising from how the positions of all the various sources of matter-and-energy move and evolve over time throughout the Universe in general, and along our lines-of-sight from the emitting source to the observer’s destination in particular.
Although there are other effects as well, these are the primary additions that must be included if we want to take that leap from special relativity, which doesn’t incorporate gravitation, to General Relativity, which does.

It’s too great of a task to presume that we can know enough about the Universe — particularly given how vast space is, how large the separations between intergalactic objects are, and how little of what’s out there we can actually observe — to reliably calculate all of these effects for each object that we observe. But what we can do is, with the parameters we can measure, determine how much each of the possible effects that could occur would actually change the answers we attempt to derive.
For example, we can measure the relative speeds of objects that are clustered closely together in space: stars within the same galaxy, galaxies within the same galaxy group or cluster, the nearest galaxies to our own, etc. When we do, we find that they’re in motion relative to one another; this motion reflects something we call peculiar velocity: motion relative to some rest frame.
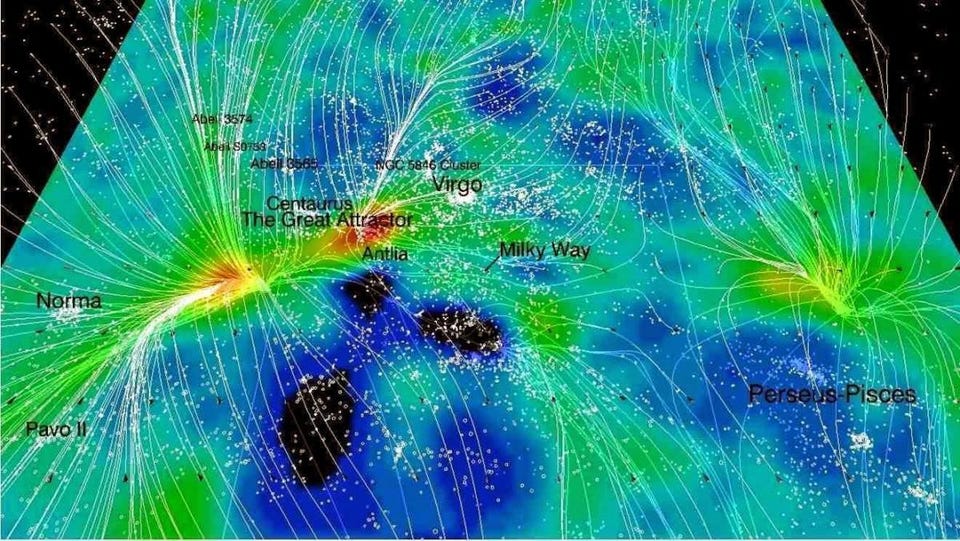
The peculiar velocities we measure typically depend on the overall mass of the largest bound structure, as individual galaxies within rich galaxy clusters can have peculiar velocities that reach up to ~2-3% the speed of light (approaching 10,000 km/s), while stars bound together in low-mass galaxies might only move at speeds of ~1 km/s relative to one another.
You can ask, for any object moving at any speed, “If I didn’t know this object’s speed, and simply mis-measured it by the amount it was actually moving, how much would that alter my estimate for how long ago the light from it was emitted?” In other words, if we assume an object is at rest, but in reality, it’s moving with a peculiar velocity of 10,000 km/s, how much would we be miscalculating the amount of time it took for light to travel from the source to the observer?
The answer, it turns out, isn’t an absolute amount of time, but rather a percentage of the total time the light had been traveling: about 0.056%. For an object whose light has been traveling for one billion years, that corresponds to an error of about ±560,000 years. With such a small contribution relative to the overall effect, we can safely ignore this effect.

Other corrections fare similarly. You can ask about gravitational redshift: the fact that when light passes through a highly curved region of space — one with a significant amount of mass all clumped together in a single dense location — light that passes through the region where curvature is the strongest will be delayed relative to light that passes through a lesser-curved (or uncurved) region.
We’ve actually had the opportunity to make a direct measurement of this effect, thanks to the power of gravitational lensing. When you have a massive enough clump of matter together in one region of space, the light from a background source is going to be bent by the presence and distribution of that mass. The mass, from the perspective of an observer looking at the background source, behaves as a lens: it can distort the light’s path, magnify it, and stretch it into odd, elongated shapes. If the alignment of the source and this mass are just right, it’s possible to even see multiple images of the same source.
In a paper published in 2021, a supernova was observed in a very distant lensed galaxy: AT 2016jka. Four images of the same galaxy could all be seen, and in three of the images, over a span of about ~6 months, the same supernova could be seen occurring at three different times.

Based on the geometry of the lens and other properties that we were able to infer, we can predict when the four images will display the same supernova once again on repeat: in the year 2037. With a time delay of ~21 years, that enables us to quantify just how much impact gravitational lensing — that is, the amount that curved space due to the presence of clustered masses — can have on light that travels through the Universe. Given that it’s a massive galaxy cluster doing the lensing, one of the most massive single, bound objects in the Universe, we can fully expect that almost all instances of the light we observe will be delayed by amounts far less than even ~1000 years.
For very nearby objects, effects like the curvature of space (which causes gravitational lensing) and peculiar velocities (which lead to special relativity’s time dilation) can be significant, and so measuring masses and velocities can be important. But on larger cosmic scales, there’s only one effect that’s dominant: the expanding Universe. As soon as light is emitted and leaves the gravitational influence of the bound structure that it’s a part of, like a galaxy or group/cluster of galaxies, it enters the intergalactic medium: the space between the galaxy. As it travels toward its ultimate destination, the observer, its wavelength not only gets stretched by the expanding Universe, but it must traverse a larger distance than it would have needed to through a static, non-expanding Universe.

This is not, as it might initially seem, a hopelessly complicated system. There are a few things that are relatively easy to measure with modern astronomical tools, including:
- how bright a distant object appears to be,
- how large, in terms of angular size, a distant light source appears to be,
- and how much, in terms of a percentage, the wavelength of the observed light is redshifted due to the expansion of the Universe.
That last point is essential, but easy to do with the science of spectroscopy. All throughout the Universe, the laws of physics are the same. This means that if you have an atom, ion, or molecule, the electron transitions that exist between the various energy levels will come at specific, calculable, measurable values, and those values will be the same for every such atom, ion, or molecule of that same species throughout the cosmos.
All you have to do is measure multiple emission or absorption lines from any distant light source, identify which atom or ion or molecule they come from, and then calculate how much the light has been stretched — or redshifted — from the originally emitted wavelength. Because, especially at large distances, the other effects can safely be neglected, you can use the redshift you measure to determine how far away an object is, and how long this light must have traveled through the expanding Universe.

When we see an object whose light has been stretched by a specific amount, we can “map” that onto how long the light has been traveling through the expanding Universe. If we also know what our Universe is made of — i.e., a mix of normal matter, dark matter, radiation, neutrinos, and dark energy — we can then translate that time into a distance, which enables us to know, at this moment, if we could travel instantaneously from one location to another, how many light-years away that object is. Here are some examples:
- Light arriving from 100 million years ago corresponds to an object that’s presently 101 million light-years away.
- Light arriving from 1 billion years ago corresponds to an object presently 1.036 billion light-years away.
- Light arriving from 5 billion years ago corresponds to an object presently 6.087 billion light-years away.
- Light arriving from 10 billion years ago corresponds to an object presently 16.03 billion light-years away.
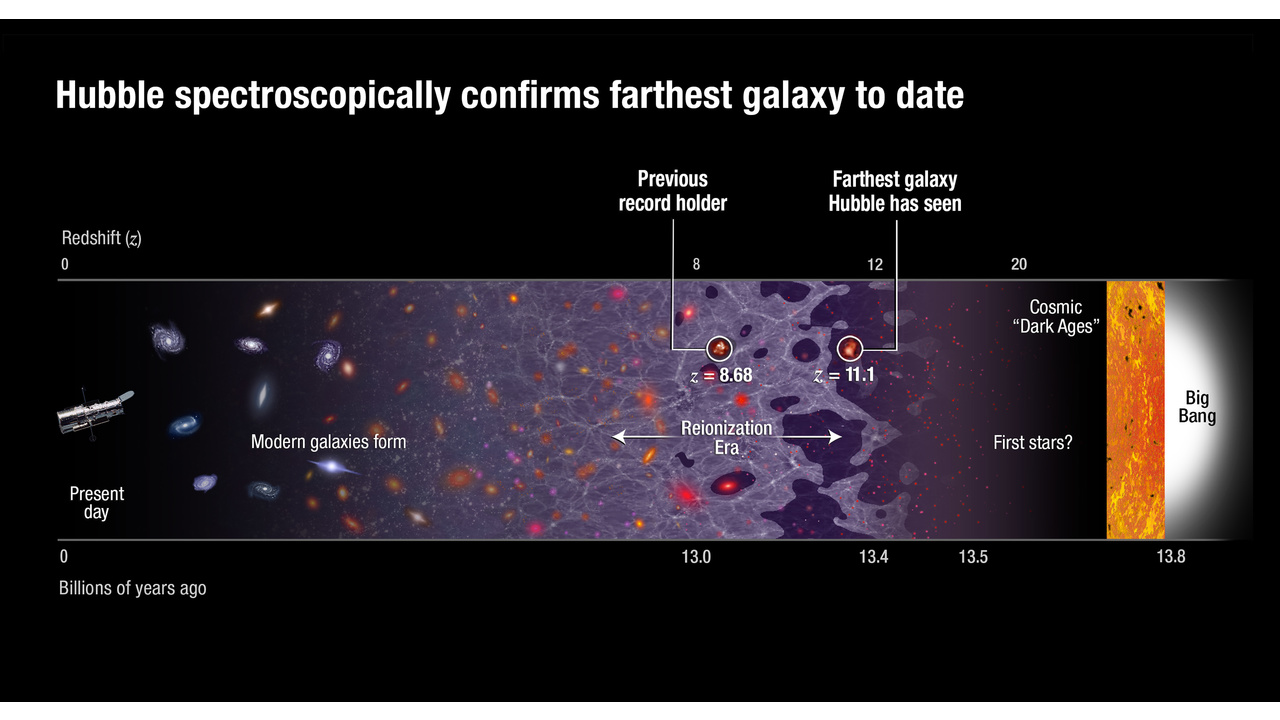
- And light arriving from 13.78 billion years ago corresponds to an object presently 41.6 billion light-years away.
At the absolute limit of the hot Big Bang, which occurred an estimated 13.8 billion years ago, we can see its leftover glow: the cosmic microwave background. Given what we know about what makes up the Universe, that “surface” that we see, in all directions, is approximately 46 billion light-years away.

The key point is not that “Relativity says there’s no such thing as simultaneity, and therefore we cannot define how much time has passed as light has traveled from one location to another.” Instead, the point is that events that appear to be simultaneous to one observer — at one moment, in one location, moving at one particular speed — won’t necessarily be simultaneous to any other observer. But using the laws of both special and general relativity, we can calculate by precisely what amount different observers, even within an expanding Universe, will disagree.
When we calculate distances and times, we’re using one particular reference frame: the reference frame in which the Big Bang’s leftover glow, the cosmic microwave background, appears to be at rest, or at the same exact temperature in all directions. As far as we can tell, aside from the dominant effect of the expanding Universe, the motion of objects within the Universe only occurs at a few hundred or thousand km/s, leading only to a fraction-of-a-percent correction to our estimates for ages and distances no matter which object we examine. Other effects, like distortions due to gravitational clumping and clustering, is even less significant.
All we have to do is choose the perspective of any observer that we can imagine, and we can determine precisely where and when, relative to them, any cosmic event that we can see has occurred.
Send in your Ask Ethan questions to startswithabang at gmail dot com!