The quantum reason behind the solidity of matter

Here on planet Earth, as well as in most locations in the Universe, everything we observe and interact with is made up of atoms. Atoms come in roughly 90 different naturally occurring species, where all atoms of the same species share similar physical and chemical properties, but differ tremendously from one species to another. Once thought to be indivisible units of matter, we now know that atoms themselves have an internal structure, with a tiny, positively charged, massive nucleus consisting of protons and neutrons surrounded by negatively charged, much less massive electrons. We’ve measured the physical sizes of these subatomic constituents exquisitely well, and one fact stands out: the size of atoms, at around 10^-10 meters apiece, are much, much larger than the constituent parts that compose them.

Protons and neutrons, which compose the atom’s nucleus, are roughly a factor of 100,000 smaller in length, with a typical size of only around 10^-15 meters. Electrons are even smaller, and are assumed to be point-like particles in the sense that they exhibit no measurable size at all, with experiments constraining them to be no larger than 10^-19 meters across. Somehow, protons, neutrons, and electrons combine together to create atoms, which occupy much greater volumes of space than their components added together. It’s a mysterious fact that atoms, which must be mostly empty space in this regard, are still impenetrable to one another, leading to enormous collections of atoms that make up the solid objects we’re familiar with in our macroscopic world.

So how does this happen: that atoms, which are mostly empty space, create solid objects that cannot be penetrated by other solid objects, which are also made of atoms that are mostly empty space? It’s a remarkable fact of existence, but one that requires quantum physics to explain.

Although human beings are made of cells, at a more fundamental level, we’re made of atoms. All told, there are close to ~10^28 atoms in a human body, mostly hydrogen by number but mostly oxygen and carbon by mass.

If you want an example of a solid object, look no further than yourself: a human being. Although you’re a collection of atoms — approximately 10²⁸ of them if you’re a full-grown adult — you’re still a solid object: you have a definitive volume and shape, and only through puncturing or severing the bonds that hold your very atoms together can another object that’s also made of atoms “pass through” you. Right now, there’s a good chance that you’re in contact with other solid objects: clothing, shoes, the floor, a chair, etc. Somehow, even though they’re mostly empty space, and even though they’re all made of the same basic constituents, atoms that are a part of you remain a part of you, and atoms that are a part of the other objects you’re in contact with remain a part of those objects.

It’s as though something is compelling the atoms that compose you to remain a part of you, while refusing to incorporate and admit atoms that are a part of some other object. Even if you were to press your thumb as hard as you could into the seat of the chair that you’re sitting on, the atoms of the chair will remain a part of the chair and the atoms of your thumb will remain a part of your thumb; these two collections of atoms will never pass through one another the way that X-rays might pass through your body’s atoms. Ever since we learned what atoms are made of, and determined that the size of the atom is much, much larger than the physical size of its constituents, we’ve been compelled to wonder why this is so.

Although, by volume, an atom is mostly empty space, dominated by the electron cloud, the dense atomic nucleus, responsible for only 1 part in 10^15 of an atom’s volume, contains ~99.95% of an atom’s mass. Reactions between internal components of a nucleus can be more precise and occur on shorter timescales, as well as at different energies, than transitions restricted to an atom’s electrons.

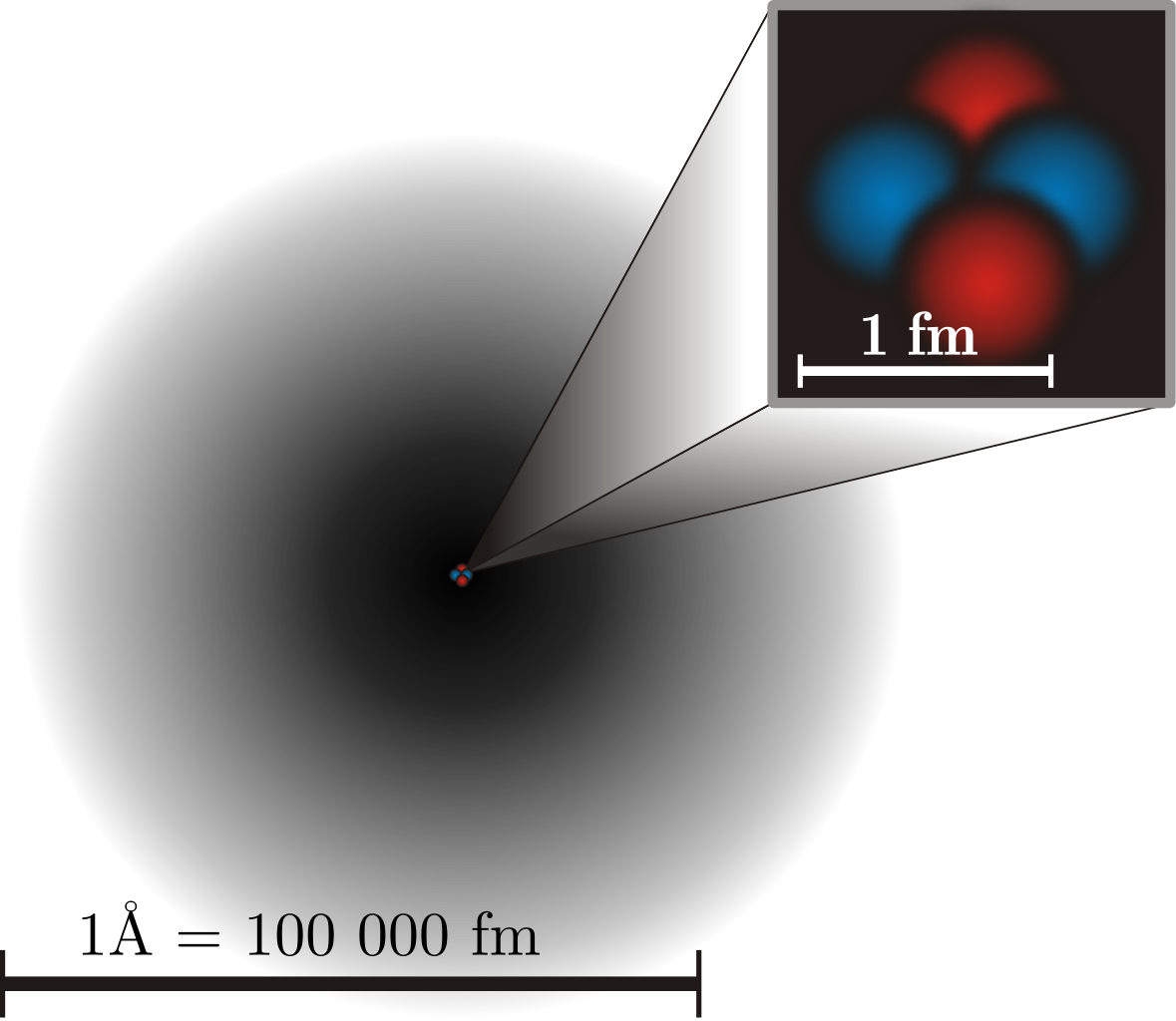
An atom, after all, is a quantum mechanical object with a massive, positively charged nucleus that’s surrounded by a very low mass, negatively charged cloud of electrons around it. While early pictures of the atom displayed a similar structure to our Solar System, we now know it’s far more accurate to view the electrons as cloud-like in nature rather than as point-like. There’s a tremendously fundamental reason for this: the fact of quantum uncertainty, and that all quanta, including electrons, exhibit wave-like behavior. In particular, every particle of matter can be described as a wave, with a characteristic wavelength scale determined by its momentum.

It’s this view of the electron, surrounding the nucleus with only a discrete set of energy levels available to it, that we typically appeal to when we talk about the size of atoms. Atoms that are more massive — i.e., that have larger numbers of protons and neutrons in their nucleus — have more electrons in orbit around them, as the number of electrons in a neutral atom always matches the number of protons in the nucleus. Because of the nature of atom-based matter, and how electrons fill atomic shells before moving on to occupy the next available energy levels, atoms with greater numbers of electrons, and with greater numbers of filled atomic shells, are generally larger in size than atoms with fewer electrons and fewer filled shells.

Although, at a fundamental level, the Universe is made up of point-like quantum particles, they assemble together to create objects of finite sizes and masses, occupying specific amounts of volume. This artist’s illustration shows several electrons orbiting an atomic nucleus, where the electron is a fundamental particle, but the nucleus can be broken up into still smaller, more fundamental constituents. Whether there are structures on scales smaller than the presently known subatomic particles remains to be discovered.

It’s these properties of atoms and of electrons that enable the chemistry that is the hallmark of Earth’s complexity. Atoms bind together based on the interactions between the electrons around their atomic nuclei, forming molecules, ions, and all sorts of intricate structures. In a great number of cases, these can build up to form macroscopic structures, where many of these structures take on solid, definitive, unchanging shapes. At their core, they may simply be large collections of atoms all bound together, but it’s the type of atom, the arrangements of those atoms, and the bonds they form with one another that all add up to determine the properties of the macroscopic object we wind up considering.

However, for any molecule, no matter how large, the story of its constituent electrons winds up being very similar to the story of even a single atom. Electrons fill the lowest-energy shells within it, with the most loosely-held electrons primarily determining the physical and chemical properties of the overall object/molecule in question. Some objects pick up electrons from their surroundings easily; other objects have their electrons easily stripped away; some objects bind together with other objects very easily to form even larger, more complex bound states. Yet, at their cores, it’s the electrons that do or don’t fill the energy levels that ultimately determine the properties of the object most significantly of all.

The atomic orbitals in their ground state (top left), along with the next-lowest energy states as you progress rightward and then down. These fundamental configurations govern how atoms behave and exert interatomic forces.

And yet, when you bring two different objects together — say, your body and the chair you’re sitting in — the atoms that compose each object remain part of each individual object under most circumstances. The two objects never pass through one another, even though they’re mostly empty space. You might think that there are two reasons for this:

• quantum uncertainty, which causes electrons to spread out over a larger volume of space,
• and electrostatic repulsion, which enables all like-charged particles, like negatively charged electrons, to repel each other.

Put these two ingredients together, and you might assume that you’ve got a recipe for atoms to create solid, independent objects.

The quantum uncertainty inherent to electrons makes them occupy a large (compared to the size of an atom’s nucleus) volume, and when you bind atoms together, those electron clouds then occupy even greater regions of space. Similarly, because the electrons occupy the outermost parts of these atoms and molecules, the act of bringing distinct objects close together means their electrons get very close to one another. Since like charges repel, and all electrons have the same negative charge inherent to them, this creates a story for how objects composed of atoms could come to be solid on macroscopic scales.

From macroscopic scales down to subatomic ones, the sizes of the fundamental particles play only a small role in determining the sizes of composite structures. Whether the building blocks are truly fundamental and/or point-like particles is still not known, but we do understand the Universe from large, cosmic scales down to tiny, subatomic ones. The scale of electrons, quarks, and gluons is the limit to how far we’ve ever probed nature: down to scales of ~10^-19 meters, where these structures remain point-like.

Unfortunately, this explanation fails completely. The combination of quantum uncertainty and electrostatic repulsion absolutely cannot account for the experience of “solid matter” here in our everyday life.

It turns out that this is related to the question of why matter is stable at all. It has to be a quantum mechanical reason; it was known way back in the 19th century that no system made up of charged particles can be stable under the laws of classical electromagnetism alone. With the advent of statistical mechanics, we came to recognize that there’s a ground-state energy, or a lowest-energy state, that any system of particles can possess. This is important, because any matter-based object is also a system of particles.

If those particles are electron-like, in the sense that they obey the statistics that electrons and particles like it do, that lowest-energy state is proportional to the number of particles in the system. However, if those particles aren’t electron-like (fermions) and are instead photon-like (bosons), the energy of that state is much greater: proportional not to the number of particles in the system but to that number raised to the 7/5 power. (First shown by Freeman Dyson in 1967, and later rigorously proven by Joseph Conlon and Elliott Lieb.) The enormous value of that energy, which still follows the rules of quantum uncertainty and electrostatic repulsion, teaches us that those two factors, alone, cannot explain the solidity or stability of matter.

This diagram displays the structure of the standard model (in a way that displays the key relationships and patterns more completely, and less misleadingly, than in the more familiar image based on a 4×4 square of particles). In particular, this diagram depicts all of the particles in the Standard Model (including their letter names, masses, spins, handedness, charges, and interactions with the gauge bosons: i.e., with the strong and electroweak forces). It also depicts the role of the Higgs boson, and the structure of electroweak symmetry breaking, indicating how the Higgs vacuum expectation value breaks electroweak symmetry and how the properties of the remaining particles change as a consequence. Neutrino masses remain unexplained.

Instead, we’re compelled to look at the difference between those two classes of particles: fermions (named after Enrico Fermi) and bosons (named after Satyendra Bose). Bosons — particles like the photon, gluon, and other particles with integer spin — follow the math you’re used to. You put one boson into a system, and you get one boson in the lowest-energy state. Put a second boson in there, and you’ve got two bosons in the lowest-energy state. Put a third boson in there, and soon there will be three bosons in the lowest energy state. And so on, until you can hear the Count’s voice from Sesame Street cackling, “Ah, ah, ah,” in your head.

Fermions, however, don’t. Particles with half-integer spin, like electrons, protons, and neutrons, obey a very different set of rules. Put one fermion into a system, and it will drop to the lowest-energy state. But put a second fermion in there, and it can only drop to the lowest-energy state if it’s a quantum state that’s unoccupied by the previous fermion(s) in there. The more fermions you add, the more “crowded” the system gets, meaning that the only way to pile more fermions in there is to have them occupy progressively higher and higher energy levels within that system. This rule for fermions was determined by Wolfgang Pauli, and the principle that underlies it — the Pauli Exclusion Principle — is one of the great unavoidable facts of our quantum Universe.

The Pauli exclusion principle prevents two fermions from coexisting in the same quantum system with the same quantum state. It only applies to fermions, however, like quarks and leptons. It does not apply to bosons, and hence there is no limit to, say, the number of identical photons that can coexist in the same quantum state. It’s why fermion-containing stellar remnants, like white dwarfs and neutron stars, can hold themselves up against gravitational collapse, as the Pauli Exclusion Principle limits the volume that a finite number of fermions can occupy.

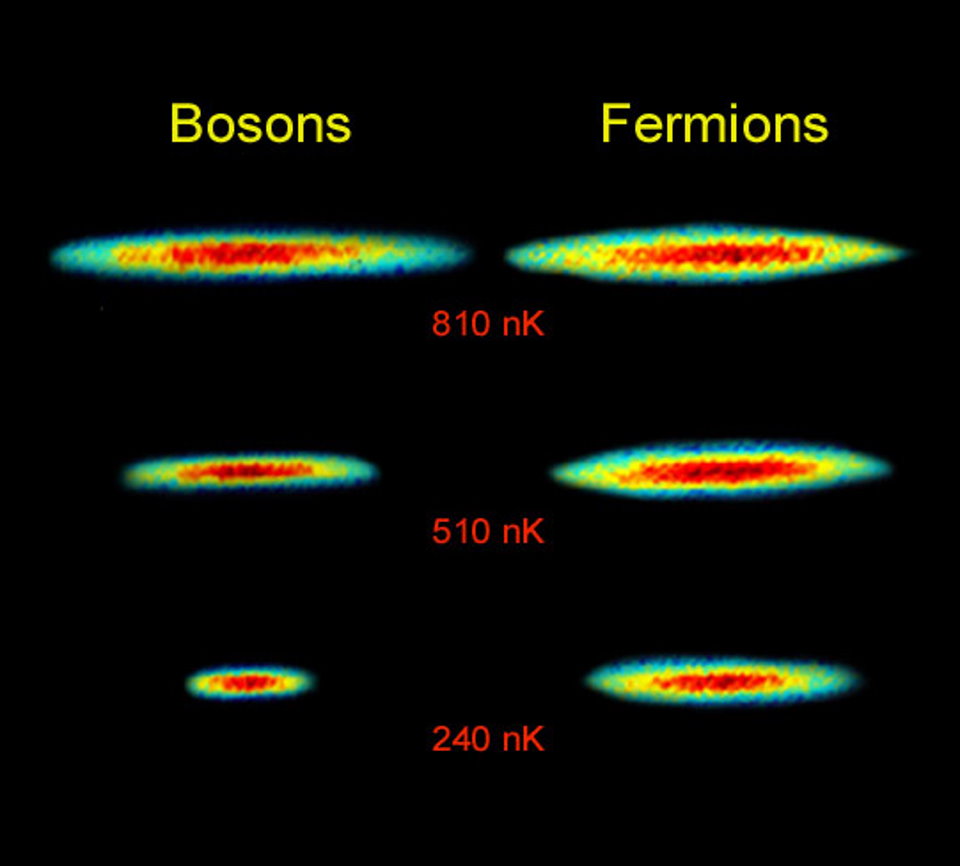
All of that is fine and dandy for each individual quantum system. But now, what happens when you bring two systems, or two objects, that are each made of atoms into contact with one another? Sure, there’s still quantum uncertainty and there’s still electrostatic repulsion, but now there’s a third critical factor at play: the Pauli exclusion rule that applies to electrons. When you push your thumb down onto the seat of your chair, the electrons in your thumb are already occupying all the lowest-energy states that are available to them. Similarly, the electrons in the chair are already occupying all the lowest-energy states available to them.

This means that the act of “pushing” your thumb into the chair is equivalent to trying to push those occupied electrons into the same quantum state as one another: to have their energy levels overlap. But those levels are full; you can’t fit anymore electrons in there! The chair’s electrons would have to be bumped up to greater energies in order to move into (or through) your thumb, and your thumb’s electrons would have to be bumped up to greater energies in order to move into (or through) your chair. No matter how strong you are, you simply don’t have enough strength in your body to overcome the Pauli Exclusion Principle in this fashion.

And that, quite simply, is how you get the property of “impenetrability” that’s inherent to solid objects.

The energy levels and electron wavefunctions that correspond to different states within a hydrogen atom, although the configurations are extremely similar for all atoms. The energy levels are quantized in multiples of Planck’s constant, but the sizes of the orbitals and atoms are determined by the ground-state energy and the electron’s mass. Only two electrons, one spin up and one spin down, can occupy each of these energy levels owing to the Pauli exclusion principle, while other electrons must occupy higher, more voluminous orbitals. When you drop from a higher energy level to a lower one, you must change the type of orbital you’re in if you’re only going to emit one photon, otherwise you’ll violate certain conservation laws that cannot be broken.

What happens, then, if you push as hard as you possibly can? It turns out that it’s actually easier to break bonds between atoms than it is for atoms to pass through one another, meaning that you’re likely to either break your chair (or break your thumb) long before you overcome the Pauli Exclusion Principle. It’s this very reason why, when you take a very sharp object, like a sharpened knife, it will “cut through” the bonds that bind atoms together, rather than simply pass through the objects that they come into contact with. The electron may be extremely humble as far as particles go, but due to its status as a fermion, it has the incredible property of forbidding all other identical fermions (i.e., other electrons) from occupying the quantum state that it happens to be in.

This type of pressure, known as degeneracy pressure, even keeps the cores of planets, stars, and stellar remnants like white dwarfs and neutron stars from collapsing. Literally the only places in the Universe where the Pauli Exclusion Principle no longer applies to objects made from atoms are black holes: where there’s so much matter condensed into such a small region of space that even light itself is forbidden from escaping from that region. That very same principle prevents atoms, despite the fact that they’re mostly empty space, from passing through each other, and in turn that gives matter its “solidity” that we’re so familiar with.

A white dwarf, a neutron star, or even a strange quark star are all still made of fermions. The Pauli degeneracy pressure helps hold up the stellar remnant against gravitational collapse, preventing a black hole from forming. Inside the most massive neutron stars, an exotic form of matter, a quark-gluon plasma, is thought to exist, with temperatures rising up to ~1 trillion (10^12) K inside.

The Pauli Exclusion Principle doesn’t only explain why matter is solid, but also why it occupies the amount of space that it does. Again: it isn’t just the uncertainty principle and electrostatic repulsion that’s responsible for volume; if matter were made of bosons, it wouldn’t occupy space in the same fashion that it does when it’s made of fermions. As I wrote earlier this year:

“The hydrogen atom is small because its electron is in the lowest-energy state allowable, the ground state, and only has one electron. Heavier atomic nuclei, however — like carbon, oxygen, phosphorus, or iron — have more protons in their nuclei, requiring greater numbers of electrons within them. If the lower-energy quantum states are all full of electrons, then subsequent electrons must occupy higher-energy states, leading to larger electron orbits (on average) and “puffier” atoms that occupy greater volumes. […] The more protons you have at the core of your atom, the more electrons you have orbiting within the outskirts of your atom. The more electrons you have, the greater the number of energy states that must be occupied. And the higher the energy state of the highest-energy electrons within your atom, the greater the amount of physical volume your atom must occupy.”

As long as matter is made up of fermions, it’s impenetrable to other objects that are also made up of the same type of fermionic matter. To those of you who thought that the Pauli Exclusion Principle wasn’t such a big deal, remember this: if it weren’t for that principle, and the fermionic nature of matter, something as simple as “sitting in a chair” would be a physical impossibility!

The author acknowledges Matt Strassler’s excellent book, Waves in an Impossible Sea, for recounting the cause of, and story behind, the experience of matter being solid and impenetrable.