Ask Ethan: Does quantum computation occur in parallel universes?

Quantum computation is, simultaneously, a remarkable scientific achievement with the potential to solve an array of problems that currently are wholly impractical to solve, and also a breathless source of wild, untrue claims that completely defy reality. In 2021, there were claims that Google’s quantum computing team developed a time crystal that violated the laws of thermodynamics. (The first part is true, the second is not.) In late 2022, a team claimed to demonstrate the existence of wormholes using a quantum computer, which was incorrect across the board. And now, here in 2024, Google has introduced a new quantum chip, Willow, that the founder and lead of Google’s Quantum AI states proves the existence of parallel universes.

Do you sense a pattern here? Are you a little suspicious of such a wild claim? Well, you should be. Whitney Clavin certainly is, as she wrote to me to ask:

“Have you seen all this crazy talk about Google’s quantum computing breakthrough providing evidence for the multiverse?! Google said this! I think you need to write a story dispelling this.”

Honestly, I am so pleased that, in an era where the news largely consists of stories where a prominent, authoritative person or group makes an outrageous claim, people are still asking the one and only question that actually matters: what’s the actual truth, here?

Please allow me to tell you.

The way solid-state storage devices work today is by the presence or absence of charged particles across a substrate/gate, which inhibits or allows the flow of current, thereby encoding a 0 or a 1. In principle, we can move from bits to qubits by having, instead of a gate with a permanent charge, a quantum bit that reads out only either a 0 or 1 when measured, but that can exist in a superposition of states while operations are being performed on it.

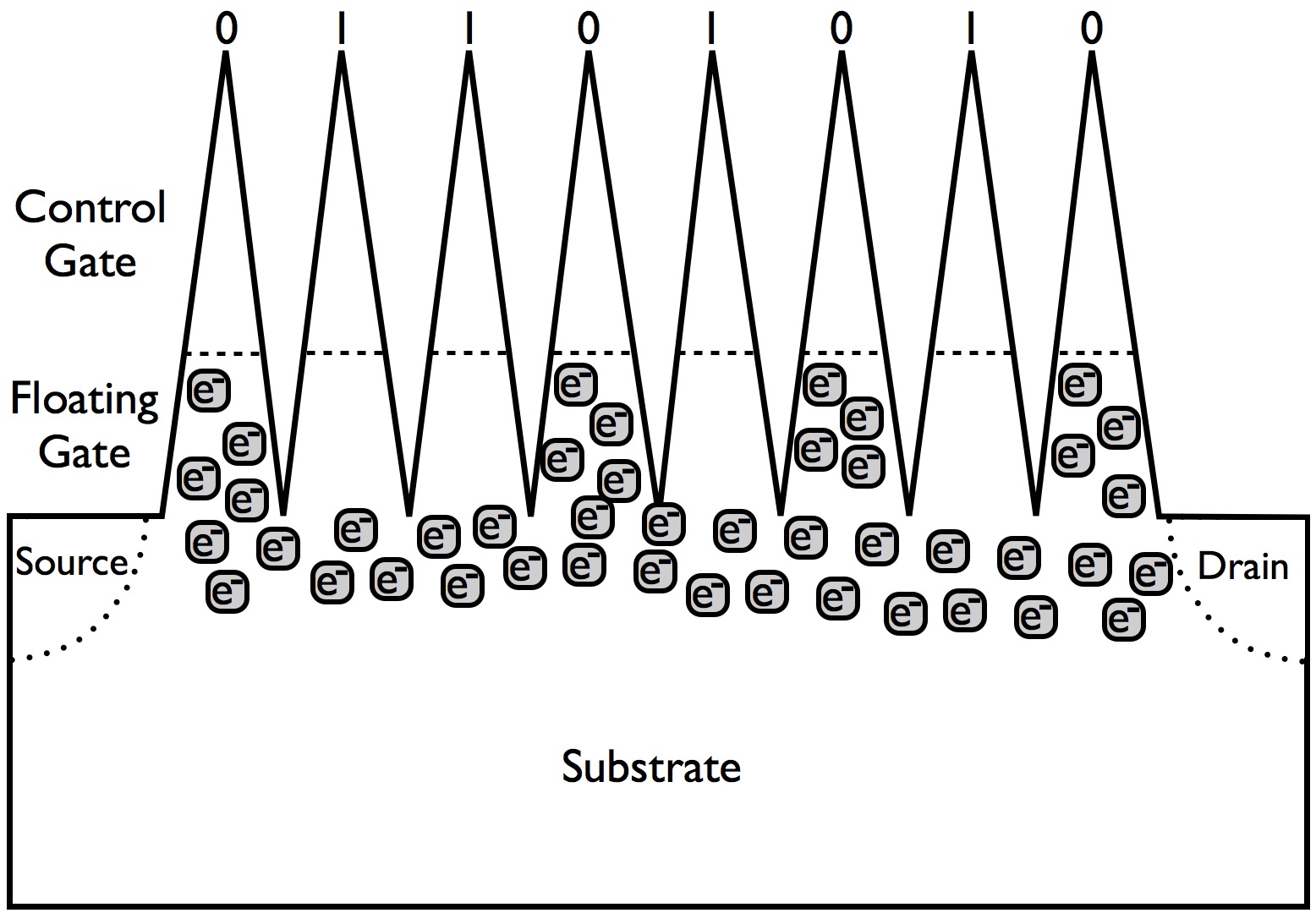
First off, quantum computers are real, and they really do hold tremendous potential to help us efficiently solve a wide class of problems that conventional — or classical — computers cannot efficiently solve. Note that the word efficiently has been emphasized, because one of the big myths about quantum computers is that they can potentially solve problems that classical computers cannot; that is not true. Any problem that can be simulated on a quantum computer can also be simulated on a classical computer; this is the core of a very famous notion in computer science: the Church-Turing thesis.

The big, fundamental difference between quantum and classical computers is simply this:

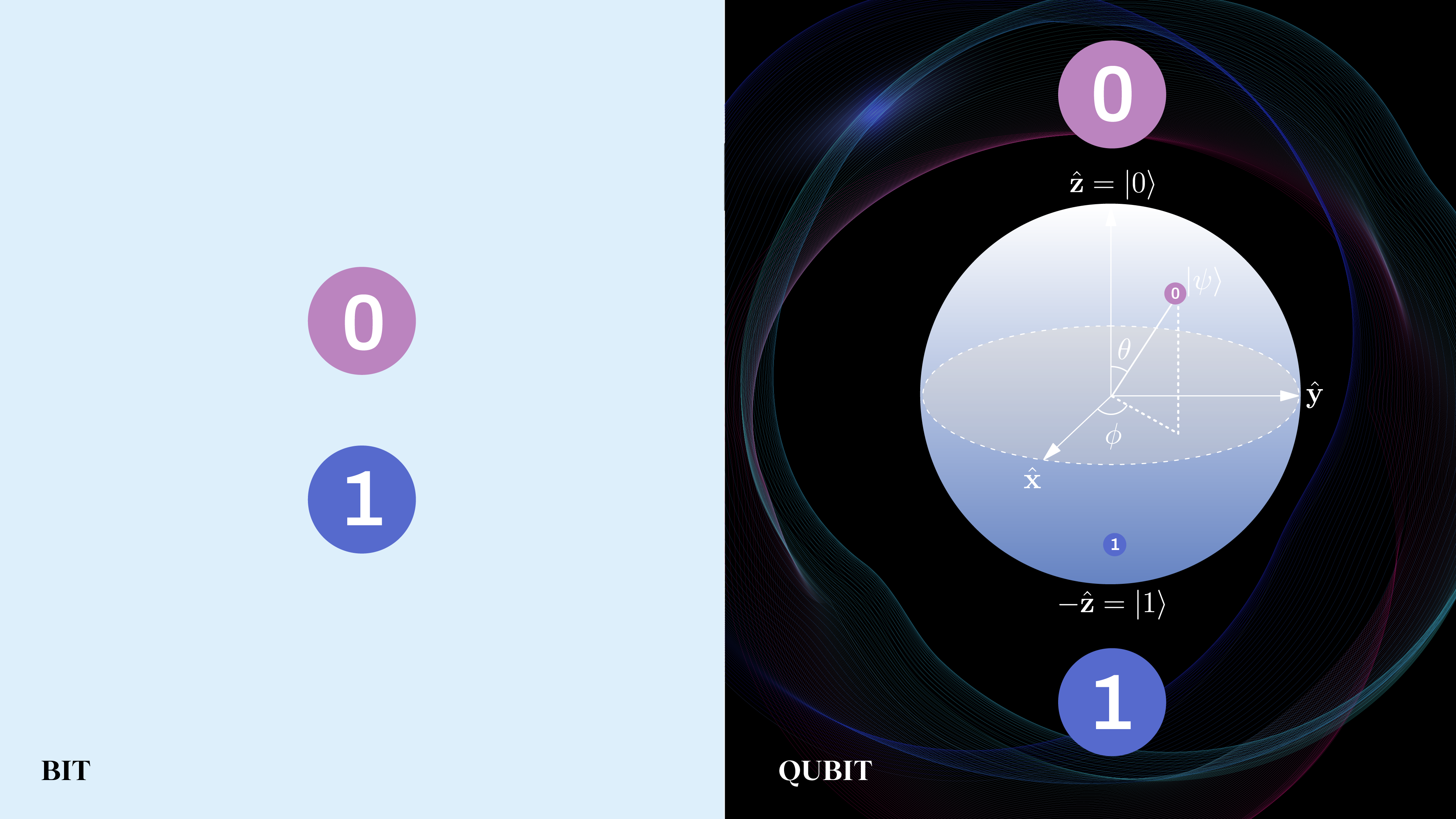
• whereas classical computers are based on bits, where all of your information is always in a binary (i.e., either a “0” or a “1”) state, both when you measure it and at the in-between times when you’re performing your computations,
• quantum computers are based on qubits, where your information always appears in a binary (“0” or “1”) state when you measure it, but at the in-between times, when you’re performing computations on it, it can exist in an indeterminate state, where it can exist in an intermediate state that’s a superposition of “0” and “1” simultaneously.

Whereas classical computers only compute using “bits,” quantum computers compute using “qubits,” giving them an extra degree of flexibility — and power — that classical computers lack.

On the left, a classical “bit” is illustrated: a two-state system that can have either “0” or “1” as its value. On the right, a quantum two-state system, or qubit, is shown. When you make a measurement, you’ll always observe either a “0” or a “1” in practice, but when you perform operations on that qubit, you act on the indeterminate state represented by the arrow shown on the sphere.

For most types of computations, these extra capabilities are completely useless. If you want to perform functions like addition or subtraction, multiplication or division, logical functions like IF, AND, OR, NOT, and so on, a classical computer can perform these functions just as efficiently as a quantum computer can; there is no advantage to using quantum computation. However, there are some classes of computation that are what we call “computationally expensive” using classical computers; they’re:

• difficult to code and require a lot of sophisticated steps,
• require large numbers of bits to encode all of the necessary information,
• require a lot of computing power to execute those steps,
• and, as a result, require enormous computing times to arrive at the result.

If you can design an algorithm (or step-by-step method) for performing a computational task, you can program it into a classical computer.

Quantum computers can do everything a classical computer can, but they can do something extra, too: instead of relying on bits, which are a two-state classical system (where everything is either in a “0” or “1” state), they are a two-state quantum mechanical system: where only two outcomes can be measured (e.g., an electron whose spin is “up” or “down”, a radioactive atom whose state is either “undecayed” or “decayed,” a photon whose polarization is “left-handed” or “right-handed,” etc.), but but where the exact quantum state remains indeterminate until that crucial measurement is made.

A qubit can exist in a state that simultaneously possesses properties of both possible states. Here, a flux qubit, or a ring made of a superconducting material, can have electric current flowing in both clockwise and counterclockwise directions simultaneously, creating a superposition of both “up” and “down” states.

This allows for fundamentally new types of computational operations (sometimes called “quantum gates”) to be leveraged in the case of quantum computers, in addition to the classical computations that they can perform.

What sorts of computational problems, then, can be solved more efficiently by a quantum computer than by a classical computer?

The answer is that there are two such classes of problems:

1. useful problems that actually have some utility, which includes simulating precisely the types of quantum systems that rely on that two-state indeterminism,
2. and useless problems that were explicitly designed because they’re computationally “cheap” for computers that can leverage qubits, two-state indeterminism, and/or fundamentally quantum gates, but that are excessively computationally expensive for classical computers.

When (or if, because it hasn’t happened yet) we can use a quantum computer to solve a useful problem faster than any classical computer can solve it, we will have achieved a remarkable milestone: quantum advantage. (Or, sometimes, practical quantum advantage.) This is likely to first arise in fields such as materials science, high-energy physics, or quantum chemistry.

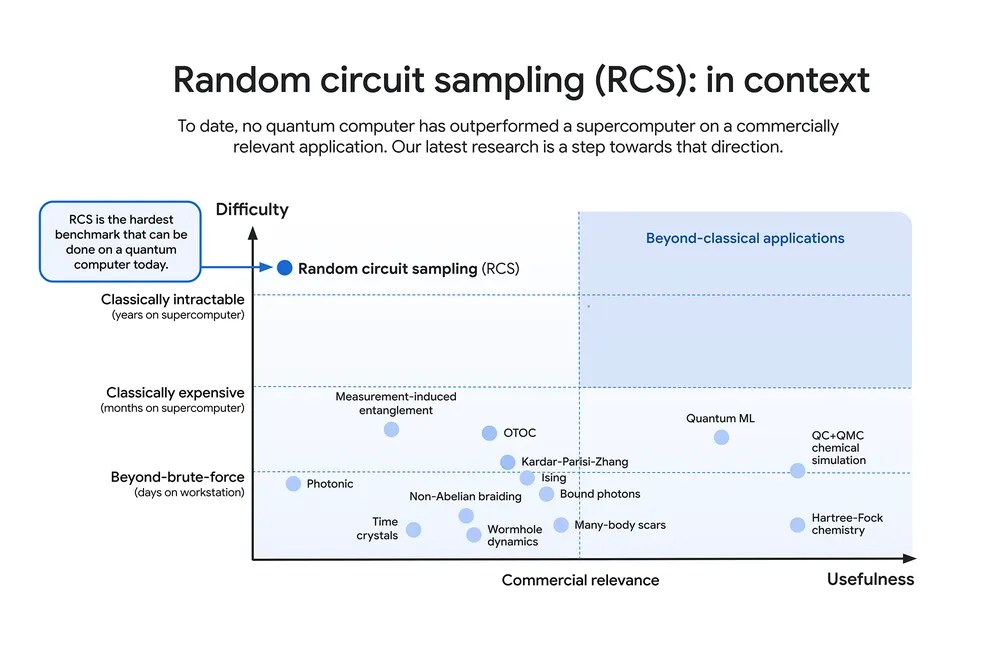
So far, however, we’ve only used quantum computers to solve fundamentally useless problems faster than classical computers: problems where quantum computers are efficient whereas classical computers aren’t, but that have no real-world utility or relevance. This demonstration has been called quantum supremacy, but is sometimes also called “quantum advantage” with no further caveats.

This rendition of a Sycamore processor mounted in a superconducting cryostat illustrates how Google’s quantum computer looked prior to the release of its Willow chip. Although qubits offer some computational advantage over classical computers, there is nothing that can be fundamentally simulated on a quantum computer that can’t also be simulated on a classical one. The goal of quantum computing is to achieve Quantum Advantage: Quantum Supremacy for a useful, practical problem.

The impractical form of quantum advantage — or quantum supremacy — was first achieved somewhere between 2017 and 2019, and has been demonstrated several times subsequently. There are three big difficulties that loom large along the road to practical quantum advantage, however.

• It’s very difficult to maintain a qubit’s quantum state; they only remain in these indeterminate states for short periods of time (tens of microseconds, at most) before an interaction with the environment leads to what’s known as quantum decoherence, ruining the “quantum-ness” of the quantum computer.
• It’s very difficult to maintain large numbers of qubits all working in tandem together; whereas modern classical computers leverage megabytes, gigabytes, terabytes, and petabytes of information (10⁶, 10⁹, 10¹², and 10¹⁵ bytes, respectively, where each byte is 8 bits), quantum computers have only now, with Google’s Willow, crossed over the 100 qubit threshold, with 105 qubits on a single quantum chip.
• And, perhaps as the greatest challenge, there’s the problem of quantum error-correction: the fact that no quantum circuit can be 100% reliable (they introduce errors), that the errors you get rise with the time needed to perform computations and the number of qubits in your circuit, and that some type of error-correction is needed to mitigate this problem.

Google’s Willow, although it’s impressively crossed the 100-qubit threshold on a single chip and performed a (fundamentally useless) calculation much more efficiently than any classical computer can, has solved a longstanding and difficult problem in quantum error-correction.

This graph shows whether problems are useful/not useful (x-axis) versus how difficult they are for classical computers to solve (y-axis). While random circuit sampling is the most difficult known task for a classical computer to achieve, it is also arguably the most useless application a quantum computer can be tasked with.

The more qubits you have, the more errors you get, right?

Not necessarily. Under certain conditions, as was demonstrated in 2023, having more physical qubits (but keeping the number of logical qubits low) can lead to vastly improved error-correction, enabling longer computational timescales before decoherence and, hence, permitting more powerful quantum computations overall.

With Willow, the Google team demonstrated that, in fact, quantum errors can be exponentially reduced as quantum computers scale up to greater and greater numbers of physical qubits. As the founder and lead of Google Quantum AI, Hartmut Neven, correctly noted:

“Willow can reduce errors exponentially as we scale up using more qubits. This cracks a key challenge in quantum error correction that the field has pursued for almost 30 years.”

That part is true, and honestly, remarkable. It’s a fantastic achievement that accelerates humanity’s progress along the road to, ultimately, some type of practical quantum advantage. We haven’t achieved that yet, however; the “benchmark” that Google’s Willow chip (and team) is touting is for a fundamentally useless problem that is notable only for how computationally expensive it is for a classical computer to perform: random circuit sampling. Sure, Willow has performed such a computation some ~10³⁰ times faster than a classical computer can, but it’s not a computation that’s in any way related to a practical use case, even in theory.

Although many claim that the advent of quantum computing will lead to a speed-up in computations across-the-board as compared to classical computers, this is wildly unlikely to be the case. Instead, the best computers will be hybrids: capable of leveraging the quantum portion for applications where Quantum Advantage can be achieved, but resorting to classical computing techniques for all other (i.e., most) applications.

If that were where the news ended, this would be a nice (and true) story about where we are on the road towards useful quantum computing. But, alas, like so many quantum computing stories that have hit the news before, this one comes along with a claim that can only be described as a white-hot searing lie, which is all the more enraging because Hartmut Neven himself has a PhD in physics (which he earned in 1996 from the Ruhr University Bocham), and should know better than to say the following:

“Willow’s performance on [the random circuit sampling] benchmark is astonishing: It performed a computation in under five minutes that would take one of today’s fastest supercomputers 10²⁵ or 10 septillion years. If you want to write it out, it’s 10,000,000,000,000,000,000,000,000 years. This mind-boggling number exceeds known timescales in physics and vastly exceeds the age of the universe. It lends credence to the notion that quantum computation occurs in many parallel universes, in line with the idea that we live in a multiverse, a prediction first made by David Deutsch.”

No.

No it doesn’t, and no it isn’t.

Quantum computation does not occur in many parallel universes; it does not occur in any parallel universes; it does not demonstrate or even hint at the idea that we live in a multiverse; and if David Deutsch agrees with this statement, then he is just as wrong as Neven is. (Which is completely, 100% wrong.)

The multiverse idea states that there are very large numbers of Universes like our own out there, and others whose properties might have extreme, fundamental differences. But in order for the many-worlds interpretation of quantum mechanics to be physically real, there must be a place (i.e., a real Universe) for these parallel outcomes to reside in, and unless inflation occurred for an infinite amount of time, the math doesn’t work out right to contain them.

There is a fundamental misunderstanding here about what parallel universes are, and it’s clearly mixed up in Neven’s head with an accompanying fundamental misunderstanding of what quantum mechanics is. There are two notions of parallel universes (or, as it’s sometimes called, the multiverse) that are relevant to our physical reality.

• There’s the inflationary multiverse, which notes that according to the theory of cosmic inflation — our theory of what preceded and set up the hot Big Bang — there isn’t just our observable Universe out there, nor merely an unobservable part to our Universe that extends beyond our cosmic horizon, but an extraordinarily large number of other “pockets” of space where inflation came to an end and triggered its own hot Big Bang, independent and separate from our own.
• There are also the parallel universes that comes along with the many-worlds interpretation of quantum mechanics. Instead of our conventional view of quantum mechanics, where reality persists in an indeterminate state (or superposition of states) of all possible outcomes until a critical measurement is made (or a critical interaction occurs), revealing just one (our) reality, the many-worlds interpretation hypothesizes that all possible outcomes actually do occur somewhere: in an infinite set of parallel universes. Moreover, with each new “measurement” (or interaction) that occurs, the timeline splits further, creating ever-increasing numbers of possible universes that we can never observe or interact with.

If each time a quantum decision were made, our timeline split to allow for two (and only two) possible outcomes, then the number of overall possibilities would increase incredibly rapidly, depending on which combinations of outcomes and what order-of-interactions are allowed. These possibilities cannot all fit within our physical, observable Universe, but the mathematical structure known as a Hilbert space can contain them all.

Quantum computing, of course, applies to neither of these. I suppose, if you wanted to be generous to Neven, you could interpret what he was saying as, “well, quantum computers are quantum systems, and since these different quantum interpretations are all physically equivalent to one another, the idea of parallel universes is consistent with my quantum computer,” which is — like quantum supremacy — true but useless.

However, because Neven explicitly stated, “It lends credence to the notion that quantum computation occurs in many parallel universes, in line with the idea that we live in a multiverse,” rather than the correct, “Our results are completely agnostic about the various interpretations of quantum mechanics, and say nothing meaningful about whether we live in a multiverse or not,” it’s hard to be that generous.

Instead, it’s likely that Neven has conflated the notion of a quantum mechanical Hilbert space, which is an infinite-dimensional mathematical space (specifically, a complex vector space) which is where quantum mechanical wavefunctions “live,” with the notion of parallel universes and a multiverse. You can have quantum mechanics work just fine, both physically and mathematically, without introducing even one parallel universe, much less an infinite number of them. You just need to both learn quantum mechanics, which Neven ought to know, and not fool yourself by conflating unrelated concepts, which Neven also ought to know.

The Many Worlds Interpretation of quantum mechanics holds that there are an infinite number of parallel universes that exist, holding all possible outcomes of a quantum mechanical system, and that making an observation simply chooses one path. This interpretation is philosophically interesting, but has no physical meaning if there isn’t enough “universe” out there to physically hold all of these possibilities within it.

It’s incredibly frustrating that a truly excellent step forward in the world of quantum computation — which enables quantum entanglement to be maintained over longer timescales and which significantly reduces the error rate of quantum computers — cannot simply be presented, even by the very team that made the advance, without packaging it alongside a howler of a statement that is true under absolutely no circumstances. This latest result has nothing to say about parallel universes, the multiverse, or the validity or invalidity of any of the still-viable interpretations of quantum mechanics.

Most importantly, it doesn’t require or even suggest that quantum computations occur anywhere other than here, right in our own Universe. Such a statement is just as foolhardy as saying that an electron that travels through a double-slit travels through that double slit in infinite parallel universes; sure, you can describe it that way, but you can describe it just as easily and successfully without appealing to anything beyond standard quantum mechanics.

Do parallel universes exist? Perhaps. Are there an infinite number of them? Also perhaps. Are they required for quantum computation, and is there any method by which quantum computers could reveal evidence for them? Absolutely not. While Hartmut Neven may be confused himself by what it all means, there’s no need to let him unnecessarily confuse you. Appreciate the result without the extraneous baggage; quantum computers have incrementally improved, and — on a completely unrelated front — parallel universes are still a fascinating but purely theoretical hypothesis and possibility.

Send in your Ask Ethan questions to startswithabang at gmail dot com!