How logic and reasoning can fail as scientific tools

- The conventional rules of logic are often used to explain practically every phenomenon in the Universe and have their roots in mathematics and deduction.
- However, they are based on certain assumptions that may not always apply in all circumstances, including notions such as cause-and-effect that don’t necessarily apply in our quantum reality.
- These three spectacular examples from the history of science show how even seemingly airtight logical arguments, like “reductio ad absurdum,” failed even great scientists in an absurd Universe.
Throughout history, there have been two main ways humanity has attempted to gain knowledge about the world: top-down, where we start with certain principles and demand logical self-consistency, and bottom-up, where we obtain empirical information about the Universe and then synthesize it together into a larger, self-consistent framework. The top-down approach is often credited to Plato and is known as a priori reasoning, with everything being derivable as long as you have an accurate set of postulates. The bottom-up approach, contrariwise, is attributed to Plato’s successor and great rival, Aristotle, and is known as a posteriori reasoning: starting from known facts and building up your model of reality from that foundation, rather than deriving them from overarching postulates.
In science, these two approaches go hand-in-hand. Measurements, observations, and experimental outcomes help us build a larger theoretical framework to explain what occurs in the Universe, while our theoretical understanding enables us to make new predictions, even about physical situations we haven’t encountered before. However, no amount of sound, logical reasoning can ever substitute for empirical knowledge. Time and time again, science has demonstrated that nature often defies logic, as its rules are more arcane than we’d ever intuit without performing the critical experiments ourselves. Here are three examples that illustrate how logic and reasoning are simply not enough when it comes to science.

1.) The nature of light. Back in the early 1800s, there was a debate raging among physicists as to the nature of light. For more than a century, Newton’s corpuscular, ray-like description of light explained a whole slew of phenomena, including the reflection, refraction, and transmission of light. The various colors of sunlight were broken up by a prism exactly as Newton predicted; the later discovery of infrared radiation by William Herschel aligned with Newton’s ideas perfectly. There were only a few phenomena that required an alternative, wave-like description that went beyond Newton’s ideas, with the double-slit experiment being chief among them. In particular, if you changed the color of the light or the spacing between the two slits, the pattern that emerged changed as well, something that Newton’s description couldn’t account for.
In 1818, the French Academy of Sciences sponsored a competition to explain light, and civil engineer Augustin-Jean Fresnel submitted a wave-like theory of light that was based on the work of Huygens — an early rival of Newton’s — to the competition. Huygens’ original work couldn’t account for the refraction of light through a prism, and so the judging committee subjected Fresnel’s idea to intense scrutiny. One of the members of the judging committee was physicist and mathematician Simeon Poisson, who through logic and reasoning, showed that Fresnel’s formulation led to an obvious absurdity.
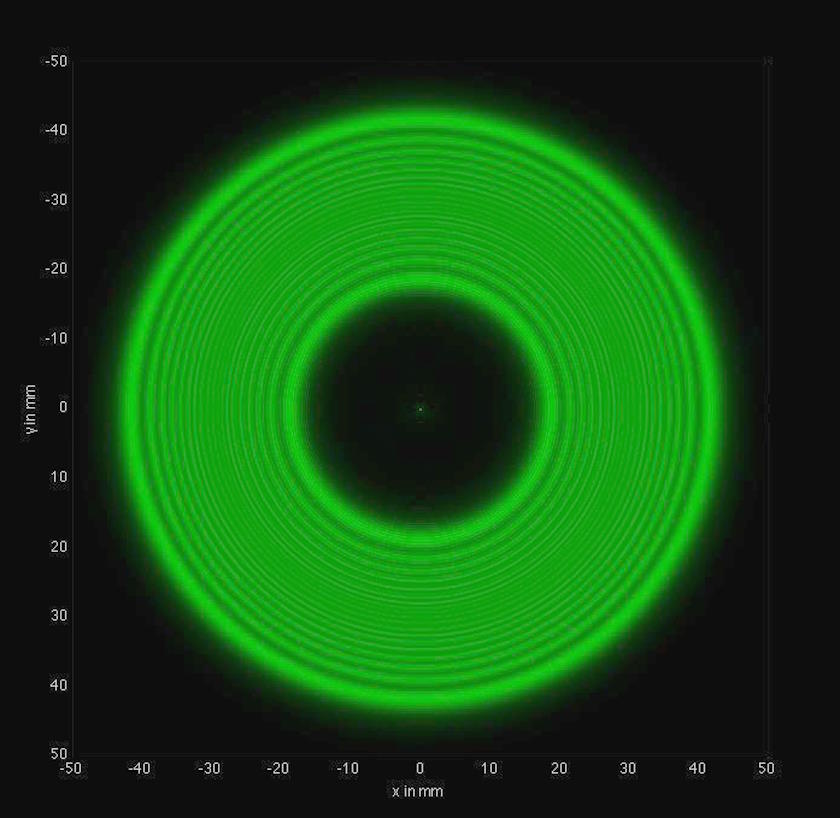
According to Fresnel’s wave theory of light, if a light were to shine around a spherical obstacle, you’d get a circular shell of light with a dark shadow filling the interior. Outside of the shadow, you’d have alternating light-and-dark patterns: an expected consequence of the wave nature of light. But inside the shadow, it wouldn’t be dark all throughout. Rather, according to the theory’s prediction, there would be a bright spot right at the center of the shadow: where the wave properties from the obstacle’s edges all constructively interfered. By showing that spherical wave patterns, if they emerged from the edge of the obstacle, would all interfere constructively at the center, the prediction implies that the central spot would be just as bright as if the obstacle weren’t even present at all!
That spot, as derived by Poisson, was clearly an absurd consequence of such a theory. Having extracted this prediction from Fresnel’s model, Poisson was certain he had, with one fell swoop of his pen, demolished the idea of the wave nature of light. If the theory of light-as-a-wave led to absurd predictions, Poisson reasoned, it must be false. Newton’s corpuscular theory had no such absurdity; it predicted a continuous, solid shadow behind the sphere, just as you would intuit.
But to Poisson’s surprise, the head of the judging committee — François Arago — chose to intervene. Not persuaded by Poisson’s calculations, Arago insisted on performing the “absurd” experiment himself.

Although this contest, and the follow-up experiment, occurred well before the invention of the laser (forbidding the use of coherent light, which could not be obtained otherwise), Arago was able to split light into its various colors and choose a monochromatic section of it for the critical experiment. He fashioned a small, spherical obstacle that the light could pass around, and shone this monochromatic light in a cone-like shape around it. Lo and behold, right at the center of the shadow, the bright spot of light that was predicted could easily be seen.
Moreover, with extremely careful measurements, a faint series of concentric rings could be seen around the central spot as well: a further vindication of the wave theory of light. Even though Fresnel’s theory led to absurd predictions, the experimental evidence, and the Spot of Arago, showed that nature obeyed these absurd rules, not the intuitive ones that arose from Newtonian reasoning. Only by performing the critical experiment itself, and gathering the requisite data from the Universe directly, could we come to understand the physics governing optical phenomena.
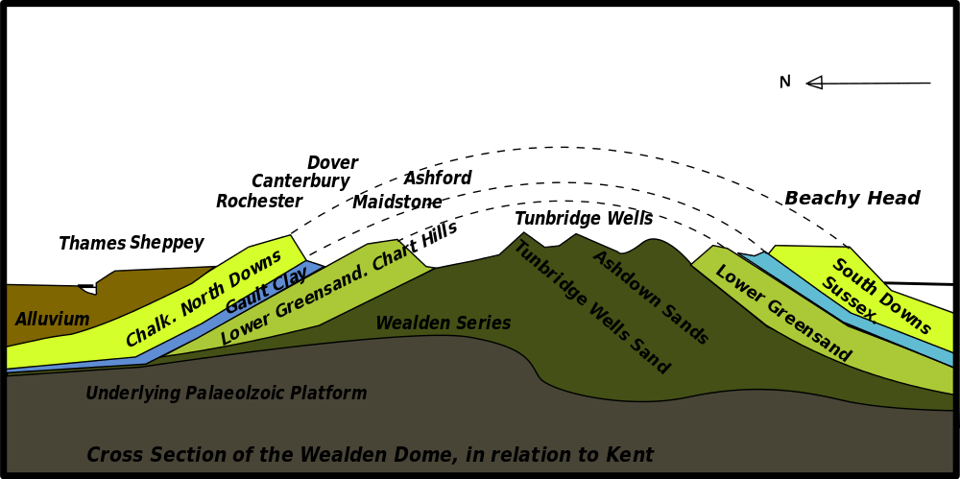
2.) Darwin, Kelvin, and the age of the Earth. By the mid-1800s, Charles Darwin was well into the process of revolutionizing how we conceive of not only life on Earth, but of the age of the Earth as well. Based on the current rates of processes like erosion, uplift, and weathering, it was clear that the Earth needed to be hundreds of millions — if not billions — of years old to explain the geological features that we were encountering. For instance, Darwin calculated that the weathering of the Weald, a two-sided chalk deposit in southern England, required at least 300 million years to create for the weathering processes alone.
This was brilliant, on the one hand, because a very old Earth would provide our planet with a long enough timeframe so that life could have evolved to its present diversity under Darwin’s rules: evolution through random mutations and natural selection. But the physicist William Thomson, who would later become known as Lord Kelvin, recognized this long duration to be absurd. If it were true, after all, the Earth would have to be much older than the Sun, and therefore the long geological and biological ages that Darwin required for the Earth must be incorrect.
Kelvin’s reasoning was very intelligent, and posed an enormous puzzle for biologists and geologists at the time. Kelvin was an expert in thermodynamics, and knew many facts about the Sun. This included:
- the Sun’s mass,
- the Sun’s distance from the Earth,
- the amount of power absorbed by the Earth from the Sun,
- and how gravitation, including gravitational potential energy, worked.
Kelvin worked out that gravitational contraction, where a large amount of mass shrinks, over time, was likely the mechanism by which the Sun shone. Electromagnetic energy (from, say, electricity) and chemical energy (from, say, combustion reactions) gave lifetimes of the Sun that were far too short: under a million years. Even if comets and other objects “fed” the Sun over time, they couldn’t produce a longer lifetime. But gravitational contraction could give the Sun its needed power output with a lifetime of 20–40 million years. That was the longest value he could obtain, by far, but it was still too short to give biologists and geologists the timescales they needed. For decades, biologists and geologists had no answer to Kelvin’s arguments.

As it turned out, though, their estimates for the ages of the Earth — both from the perspective of the timescales required for geological processes and the time necessary for evolution to give us the diversity of life we observe today — were not only correct, but conservative. What Kelvin didn’t know was that nuclear fusion powered the Sun: a process entirely unknown during Kelvin’s time. There are stars that get their energy from gravitational contraction, but those are white dwarfs, which are thousands of times less luminous than Sun-like stars, and shine for far longer than any Sun-like star can under the power of nuclear fusion.
Even though Kelvin’s reasoning was sound and logical, his assumptions about what powered the stars, and hence, his conclusions about how long they lived, were flawed. It was only by uncovering the physical process that underpinned these luminous, heavenly orbs that the mystery was solved. Yet that premature conclusion, which rejected the geological and biological evidence on the grounds of absurdity, plagued the scientific discourse for decades, arguably holding back a generation of progress.

3.) Einstein’s greatest blunder. In late 1915, a full decade after putting his theory of special relativity out into the world, Einstein published a new theory of gravity that would attempt to supersede Newton’s law of universal gravitation: general relativity. Motivated by the fact that Newton’s laws couldn’t explain the observed orbit of the planet Mercury, Einstein embarked to create a new theory of gravity that was based on geometry: where the fabric of spacetime itself was curved owing to the presence of matter and energy.
And yet, when Einstein published it, there was an additional term in there that practically no one anticipated: a cosmological constant. Independent of matter and energy, this constant acted like a large-scale repulsive force, preventing matter on the largest scales from collapsing into a black hole. Many years later, in the 1930s, Einstein would recant it, calling it “his greatest blunder,” but he originally included it in the first place because, without it, he would have predicted something completely absurd about the Universe: it would have been unstable against gravitational collapse.

This is true: if you start with any distribution of stationary masses under the rules of general relativity, it will inevitably collapse to form a black hole. The Universe, quite clearly, has not collapsed and is not in the process of collapsing, and so Einstein — realizing the absurdity of this prediction — decided that he had to throw this extra ingredient it. A cosmological constant, he reasoned, could push space apart in exactly the fashion needed to counteract the large-scale gravitational collapse that would otherwise occur.
Although Einstein was correct in the sense that the Universe wasn’t collapsing, his “fix” was an enormous step in the wrong direction. Without it, he would have predicted (as Friedmann did in 1922) that the Universe must be either expanding or contracting. He could have taken Hubble’s early data and extrapolated the expanding Universe, as Georges Lemaître did in 1927, as Howard Robertson did independently in 1928, or as Edwin Hubble himself did in 1929.
As it happened, though, Einstein wound up deriding Lemaître’s early work, commenting, “Your calculations are correct, but your physics is abominable.” Indeed, it was not Lemaître’s physics, but Einstein’s seemingly logical and reasonable assumptions, and the conclusions that came out of them, that were abominable in this instance.

Look at what all three cases have in common. In every instance, we came into the puzzle with a very good understanding of what the rules were that nature played by. We noticed that if we imposed new rules, as some very recent observations seemed to imply, that we’d reach a conclusion about the Universe that was clearly absurd. And that if we had stopped there, having satisfied our logical minds by making a reductio ad absurdum argument, we would have missed out on making a great discovery that forever changed how we made sense of the Universe.
The important lesson to take away from all of this is that science is not some purely theoretical endeavor that you can engage in by divining the rules from first principles and deriving the consequences of nature from the top-down. No matter how certain you are of the rules governing your system, no matter how confident you are in what the pre-ordained outcome will be, the only way we can gain meaningful knowledge of the Universe is by asking quantitative questions that can be answered through experiment and observation. As Kelvin himself so eloquently put it, perhaps learning the ultimate lesson from his earlier assumptions,
“When you can measure what you are speaking about, and express it in numbers, you know something about it; but when you cannot measure it, when you cannot express it in numbers, your knowledge is of a meager and unsatisfactory kind.”