LIGO’s Lasers Can See Gravitational Waves, Even Though The Waves Stretch The Light Itself

If you think about the way a gravitational wave detector works, you might encounter a paradox. Here’s the solution.

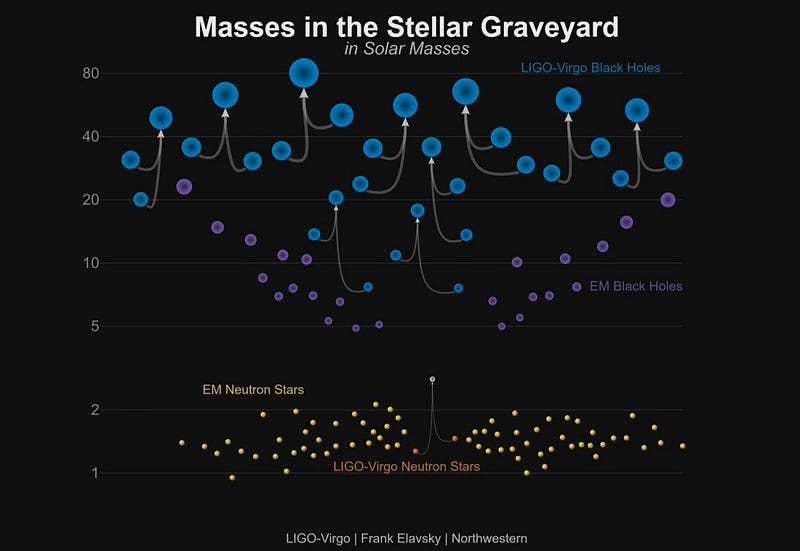
One of the greatest scientific achievements in all of human history was at last achieved just a few years ago: the direct detection of gravitational waves. Although they were an early prediction teased out of Einstein’s General Relativity put out all the way back in 1915 it took a full century for them to be directly discovered.

The way we accomplished this dream is through a remarkable design shared by the LIGO, Virgo, and KAGRA detectors:

• splitting light so that it travels down two mututally perpendicular laser-arms,
• reflecting that light back-and-forth multiple times in rapid succession,
• and then recombining the beams to see an interference pattern.

When a sufficiently strong gravitational wave passes through with the right frequency to be detected, the arms alternately expand and contract, altering the interference pattern. But won’t the light expand and contract, too? The surprising answer is “no,” and this is the reason why.

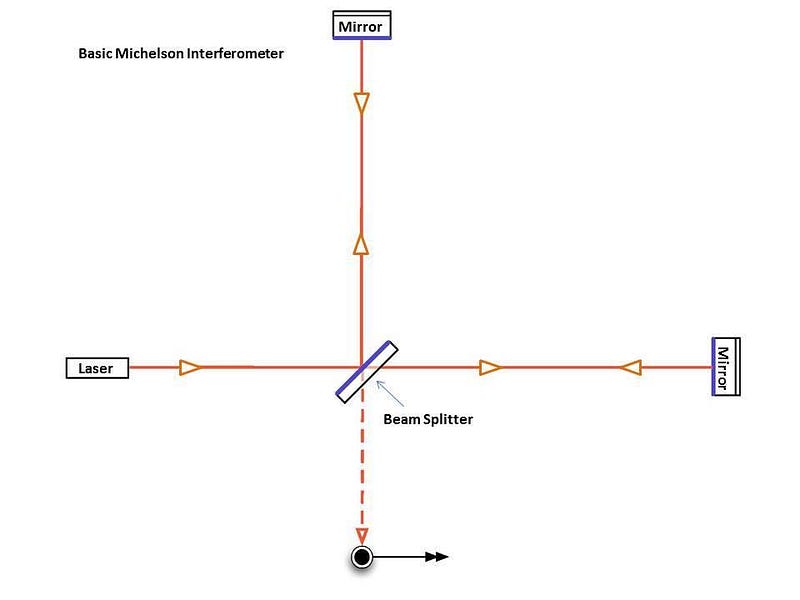
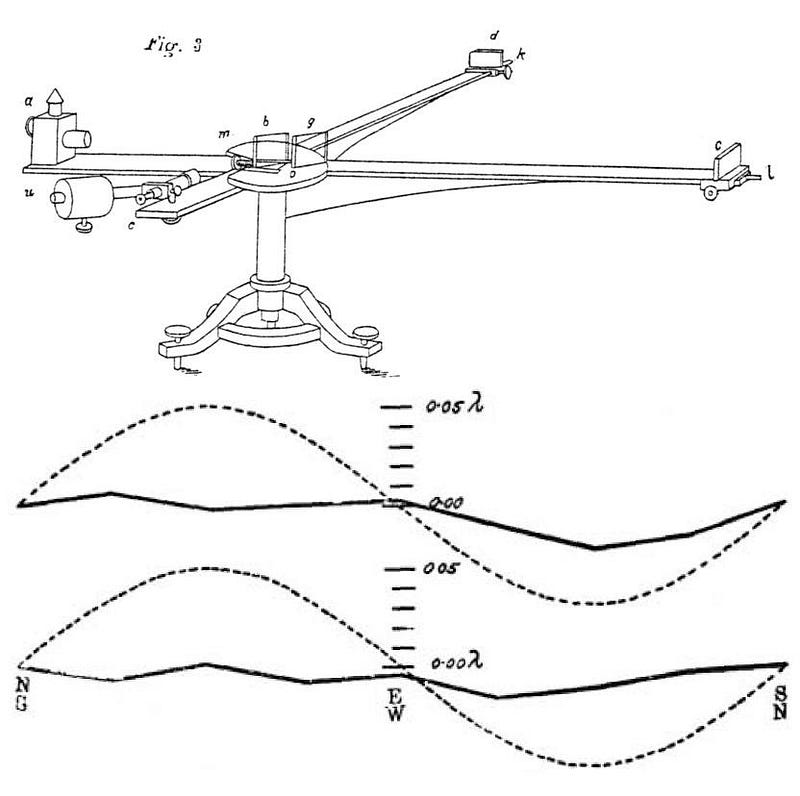
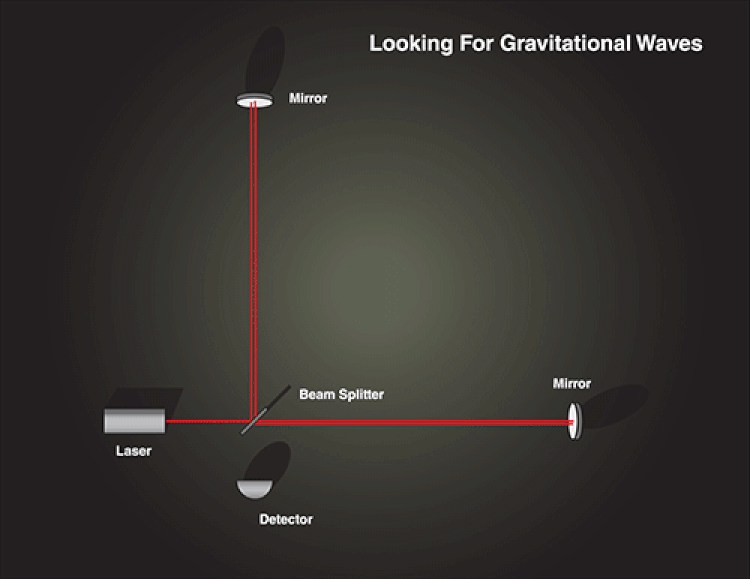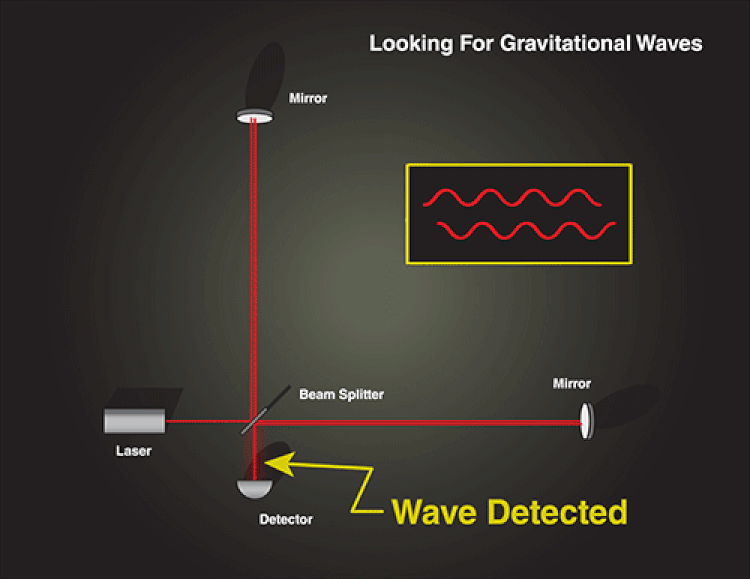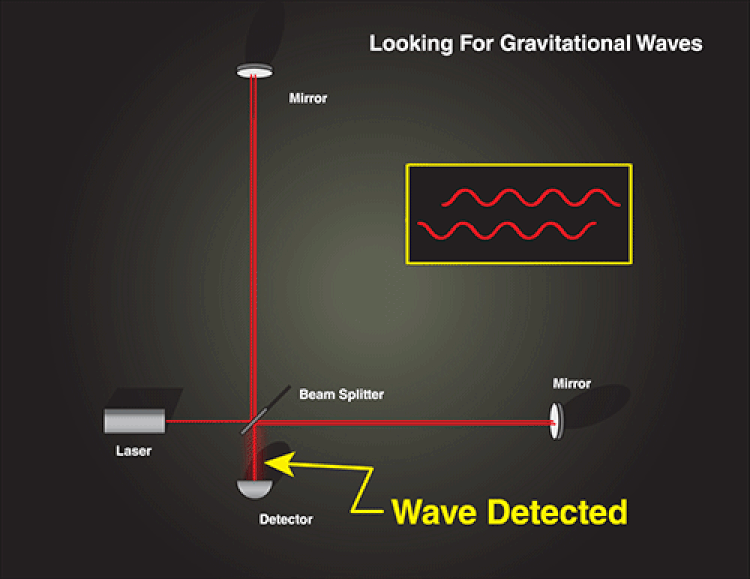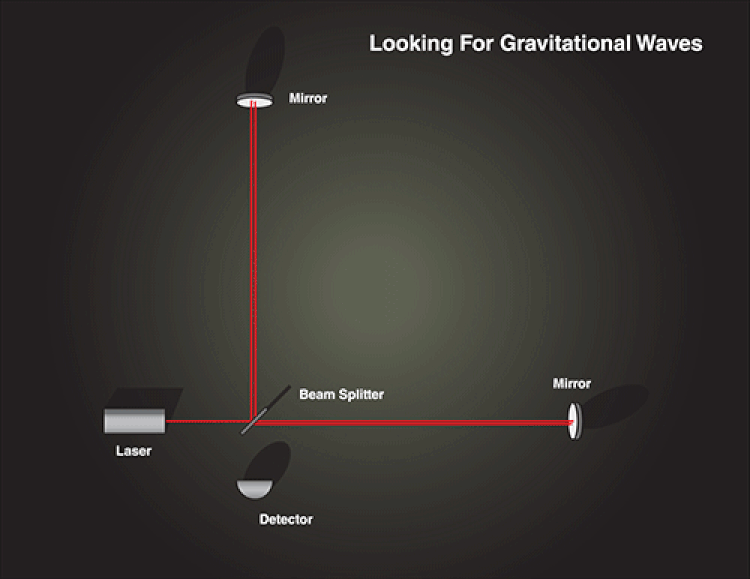
The above diagram shows off what a Michelson interferometer is: a very old device that was designed for an entirely different purpose. In 1881, Albert Michelson sought to detect the aether, which was hypothesized to be the medium that light waves traveled through. Before Special Relativity arrived, all waves were assumed to need a medium to travel through, like water waves or sound waves.

Michelson built such an interferometer using the reasoning that the Earth was traveling through space — around the Sun — at about 30 km/s. Since the speed of light was 300,000 km/s, he estimated that he’d see the interference pattern produced by the interferometer that depended on what angle the apparatus was aligned at with respect to the Earth’s motion.

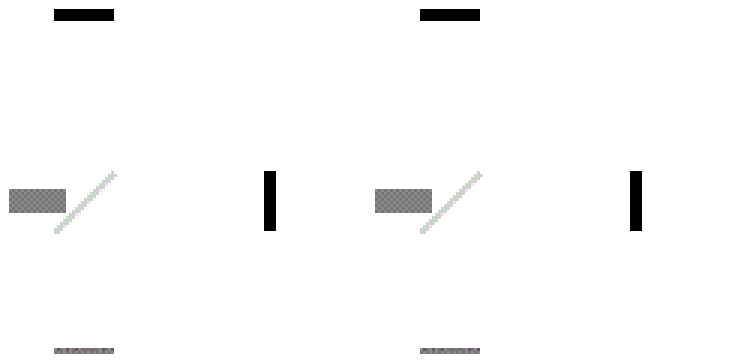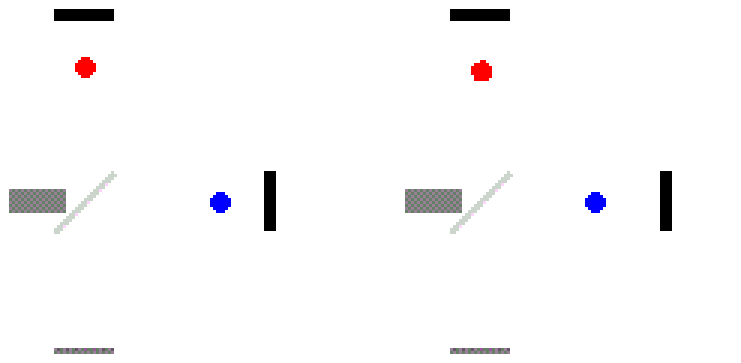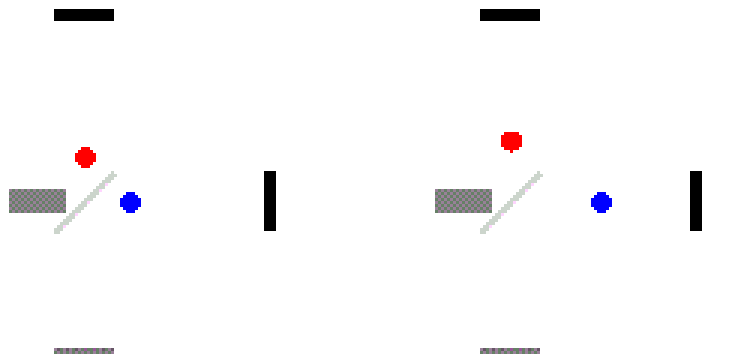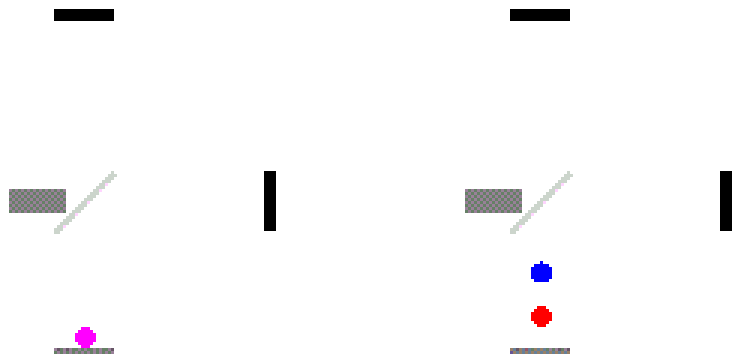
By 1887, he had performed the experiment to much better precision than the expected magnitude of the effect: about 40 times better. Yet he only ever achieved a null result, which demonstrated that the aether didn’t exist, not at least the way physicists were thinking about it. Michelson was awarded the Nobel Prize in Physics in 1907, arguably the only time that the prize was given for an experimental “null result.”

This provided evidence that the speed of light is the same for all observers, independent of any other motion along, opposed to, perpendicular to, or at any arbitrary angle relative to the direction the light propagates in. As long as the interference pattern is created in one particular orientation, it should be unchanged regardless of how you orient your detector.

However, lengthening or shortening one arm, relative to the other, will change the path length, and will therefore change the interference pattern that we see. If one were to move the mirror on the far end either closer to or farther away from the near end, there will be a slight change in the peak-trough-peak-trough pattern that the wave makes. But if you keep your apparatus stable, with constant arm lengths, that pattern should not change at all.

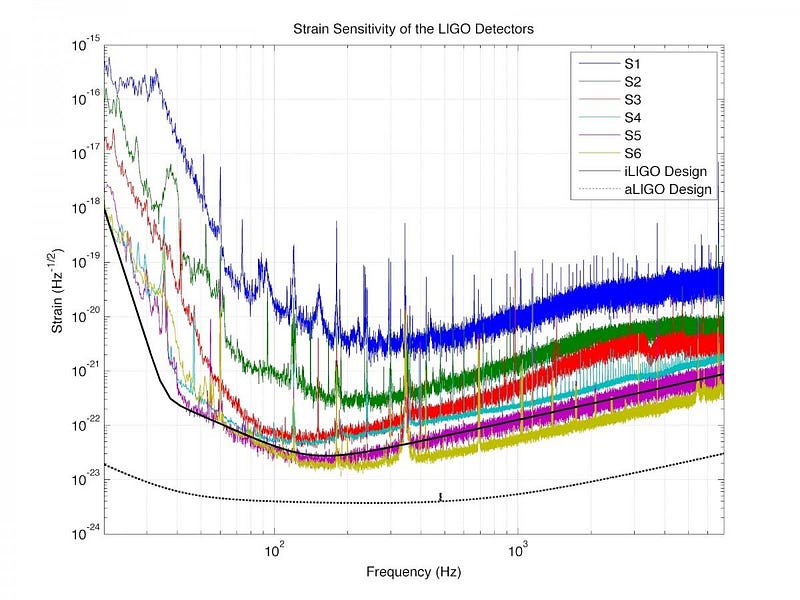
In order to set up a gravitational wave experiment in the first place, these are the conditions you need to meet. You must configure and calibrate your detector properly, account for noise from all sources, and bring your sensitivity level down to a point where it could conceivably detect the tiny arm-length changes that a gravitational wave would induce. After decades of effort, the LIGO collaboration was the first gravitational wave detector to reach a noise threshold that could lead to a physical, observable effect.

You might have heard that light is a wave: an electromagnetic wave. Light consists of in-phase, oscillating, mutually perpendicular electric and magnetic fields, and those fields interact with any matter that couples to electromagnetism in its vicinity.

Similarly, there’s a gravitational analogue: gravitational waves. These ripples move through space at the same speed as light, c, but don’t produce detectable signatures that arise from an interaction with particles. Instead, they alternately stretch-and-compress the space they pass through in mutually perpendicular directions. As a gravitational wave passes through a region of space, any volume of space experiences an expansion in one dimensions accompanied by a rarefaction (or compression) in the perpendicular direction. The wave then oscillates with a frequency and amplitude, like any other wave.

This is the reason why our gravitational wave detectors have been constructed with perpendicular arms: so that when a wave passes through them, the two different arms will experience different effects. When a gravitational wave passes through, one arm compresses while the other expands, and then vice versa.

Accounting for the curvature of the Earth, LIGO, Virgo, and KAGRA detectors are all at angles to one another. With all of them operational at once, no matter what the incoming wave’s orientation is, multiple detectors will be sensitive to the gravitational wave signal. As long as the wave itself passes through the detector — and there is no known way to shield yourself from a gravitational wave — it should affect the path length of the arms in a detectable fashion.

But this is where the puzzle comes in: if space itself is what’s expanding or compressing, then shouldn’t the light moving through the detectors be expanding or compressing too? And if that’s the case, shouldn’t the light travel the same number of wavelengths through the detector as it would have if the gravitational wave had never existed?

This seems like a real problem. Light is a wave, and what defines any individual photon is its frequency, which in turn defines both its wavelength (in a vacuum) and its energy. Light redshifts or blueshifts as the space it’s occupying stretches (for red) or contracts (for blue), but once the wave has finished passing through, the light returns to the same wavelength it was back when space was restored to its original state.

It seems as though light should produce the same interference pattern, regardless of gravitational waves.

And yet, the gravitational wave detectors really work! Not only do they work, but they’ve identified the explicit signatures of black hole-black hole mergers, allowing us to reconstruct their masses pre-merger and post-merger, their distances, their locations in the sky, and to many other properties.

The key to understanding this is to forget about wavelength and to focus on time. Yes, wavelength really is dependent on how space changes as a gravitational wave passes through; those redshifts and blueshifts are real. But what doesn’t change is the speed of light in a vacuum, which is always 299,792,458 m/s. (And the laser cavities for these gravitational wave machines offers the best human-created vacuum of all-time.) If you compress one of your arms, the light-travel time shortens; if you expand it, the light-travel time lengthens.

And, as the relative arrival times change, we can see an oscillatory pattern emerge in how the (reconstructed) interference pattern shifts over time during a real gravitational wave event.

When the two perpendicular beams, which were separated at the start of each laser pulse, reunite in the detector, they create the critical interference pattern we observe. If there’s a difference in arm length at any point, then there will be a difference in the amount of time these beams have been traveling, and hence the interference pattern will shift.

This is why we use beams rather than individual photons. If a pair of photons are emitted simultaneously and travel down the perpendicular arms, the one that sees the shortest cumulative path-length will arrive first: before its partner photon, which will see a longer cumulative path length.

But waves are continuous sources of light. Even though the arrival time differs by just ~10^-27 seconds, that’s enough to cause the two waves, initially tuned to cause the interference pattern to disappear, to appear in a spectacularly oscillating mismatch, producing the critical signal.

You might still be worried about the redshift and blueshift effects of the light, but they can be ignored for two reasons.

1. Even though the light’s wavelength changes during its journey, all light of all wavelengths, at least in a vacuum, travel at the same speed.
2. Even though the light’s wavelength changes from point-to-point, those changes are transient; when they arrive at the detector, at the same point in space, they’re going to be the same wavelength once again.

This is the key, important point in all of this: red light (of long wavelengths) and blue light (of short wavelengths) both take the same amount of time to traverse the same distance.

The fact is that when a gravitational wave passes through a detector, it changes the relative path-length of the two mutually perpendicular arms. The change in path length changes the required light-travel-time of each quantum of light, which results in different arrival times and causes a shifting in the interference pattern that results. As both arm lengths change together, in phase, we can use that information to reconstruct properties of the gravitational waves generated at the distant source.

The critical component to understanding how it works is that one beam of light spends slightly longer in the apparatus, and so when it arrives at the detector, it’s slightly out-of-phase with its counterpart. That tiny time shift, arising from the fact that LIGO’s (and Virgo’s, and KAGRA’s) arms compress by about 0.01% the width of a proton, is presently being used to find dozens of new merger events during the current Run III. Gravitational wave is now a robust, observational science, and now you know how its detectors actually work!