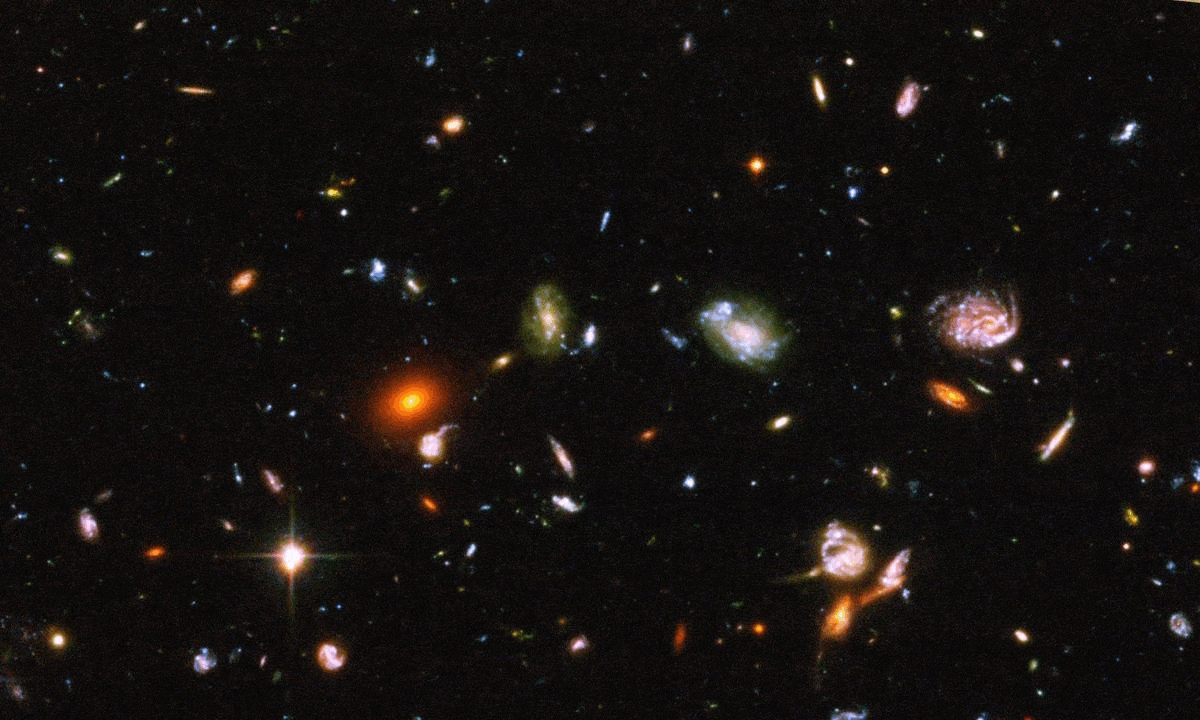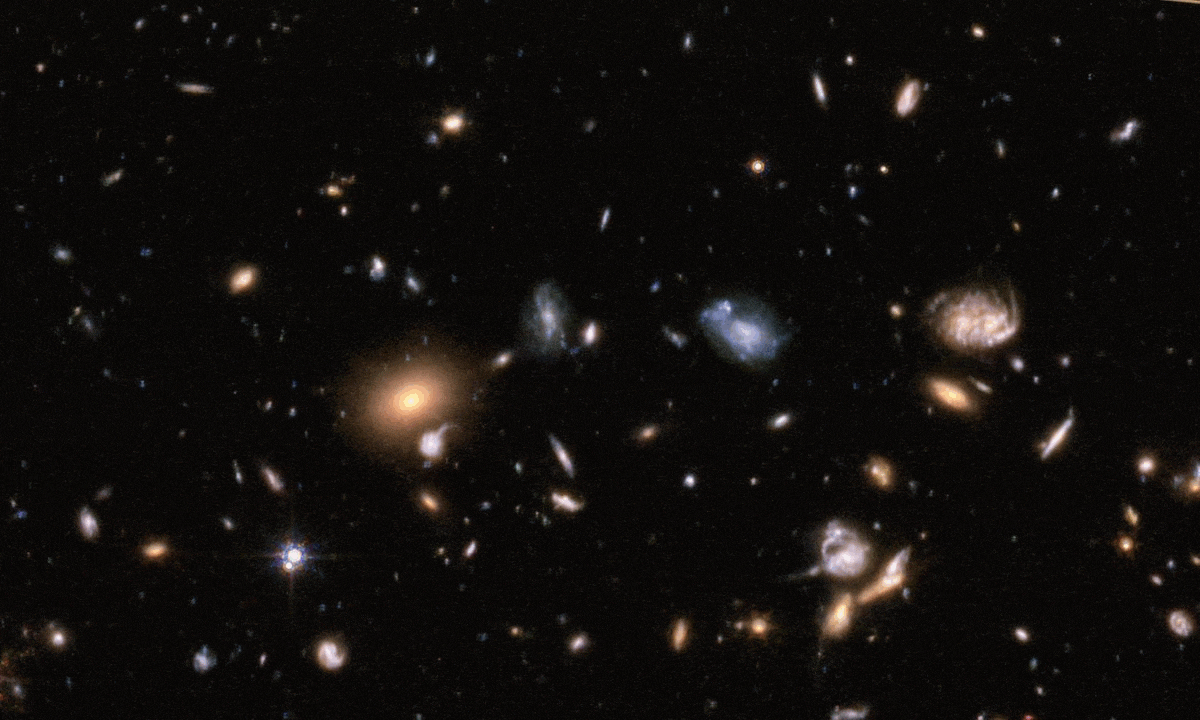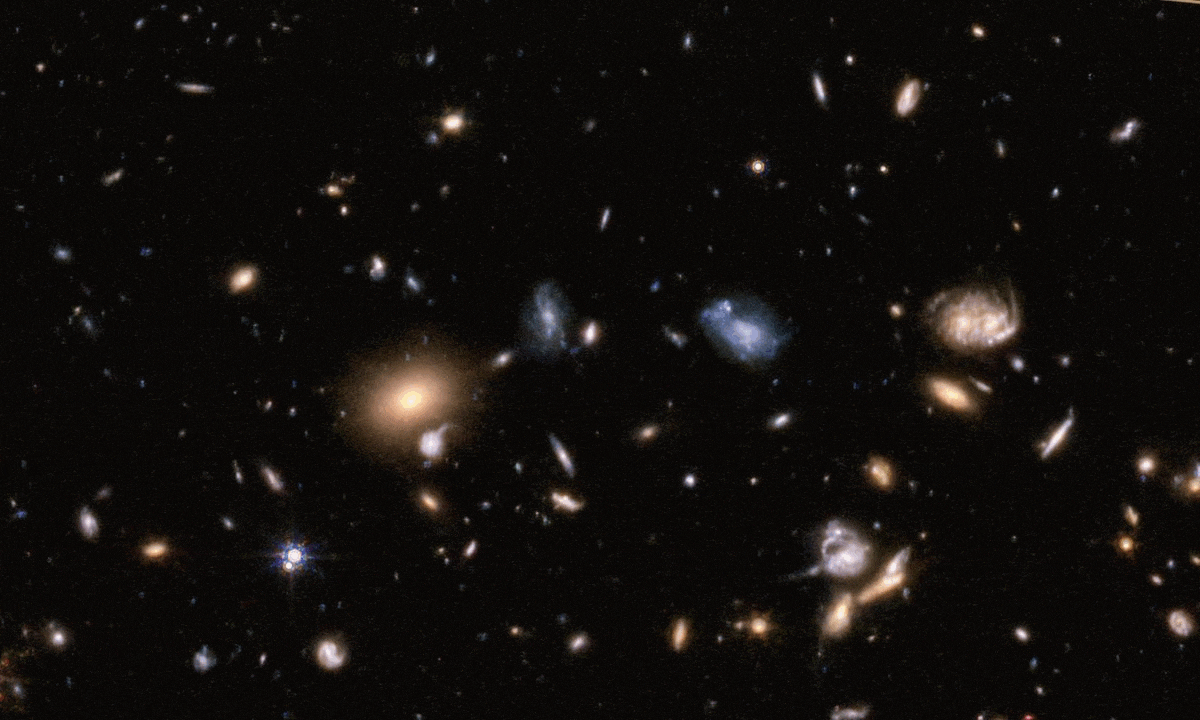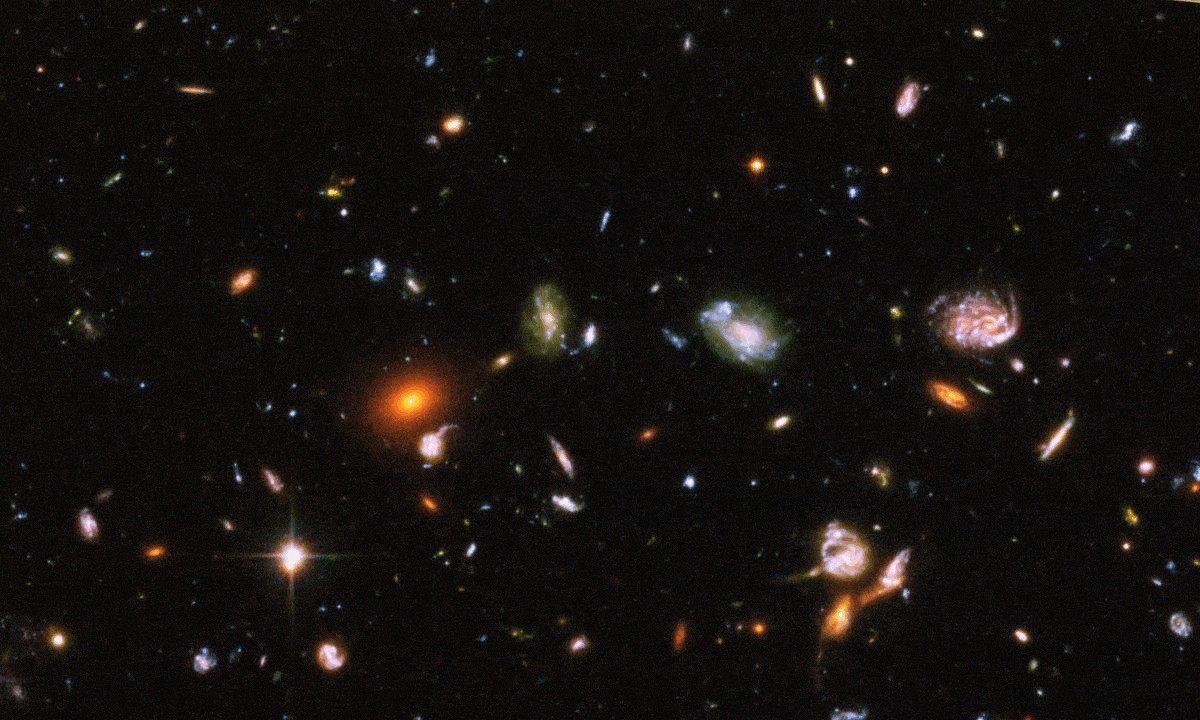How Quantum Physics Allows Us To See Back Through Space And Time

If it weren’t for a subatomic quantum rule, our Universe would be vastly different.

In many ways, our views of the distant Universe are the closest things we’ll ever get to having a time machine. While we cannot travel back through time, we can do the next best thing: view the Universe not as it is today, but rather as it was a significant amount of time ago. Whenever light is emitted from a distant source — like a star, galaxy, or quasar — it first needs to traverse the vast cosmic distances separating that source from ourselves, the observer, and that takes time.

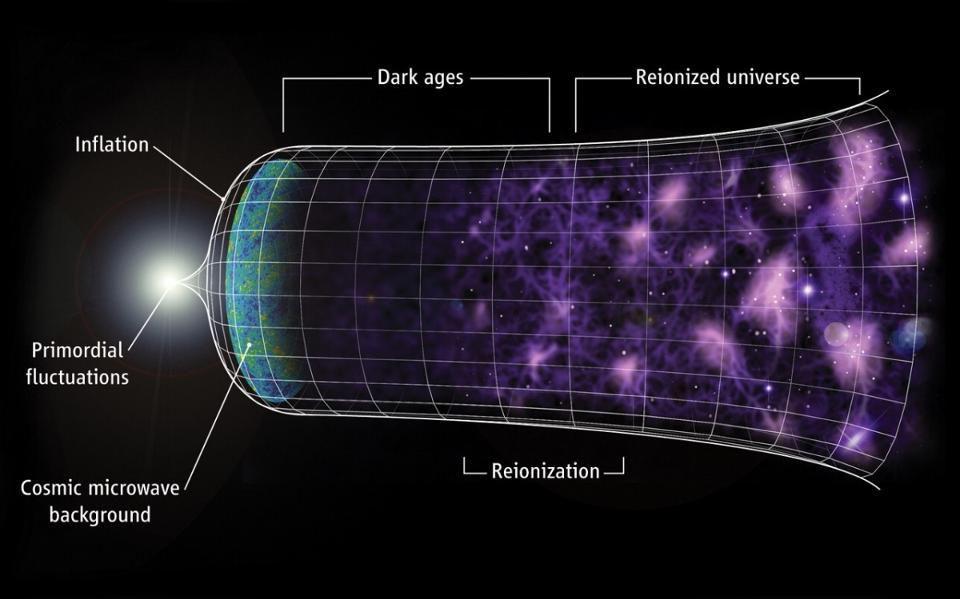
Even at the speed of light, it can take billions or even over ten billion years for those signals to arrive, meaning that the farther away we see a distant object, the closer back in time towards the Big Bang we’re looking. The earliest light we can see, however, comes from a time before any stars or galaxies: when the Universe’s atomic nuclei and electrons combined to form neutral atoms. Yet it’s only a very specific quirk of quantum physics that allows us to see the Universe as it was so long ago. Without it, the earliest signals wouldn’t exist, and we’d be unable to look as far back through space and time as we can today. Here’s how quantum physics allows us to see so far back in space and time.

To understand where the earliest observable signal in the Universe comes from, we have to go way back in time: to the earliest instants of the Big Bang. Back when the Universe was hot, dense, almost perfectly uniform, and filled with a mix of matter, antimatter, and radiation, it was expanding incredibly rapidly. In these earliest moments, there were regions of the Universe that were slightly denser than average and regions that were slightly less dense than average, but only by ~1 part in 30,000.

If it were up to gravity alone, the overdense regions would grow, attracting more of the surrounding matter than the average or underdense regions, while the underdense regions would give up their matter to its denser surrounding regions. But the Universe isn’t governed only by gravity; the other forces of nature play an important role. Radiation, for example — particularly in the form of photons — is extremely energetic in the early Universe, and its effects on how matter evolves are important in a number of ways.

First off, matter (and antimatter), if it’s electrically charged, will readily scatter off of photons. This means that any quantum of radiation, anytime it encounters a charged particle, will interact and exchange energy with it, with encounters being more likely with low-mass charged particles (like electrons) than high-mass ones (like protons or atomic nuclei).

Second off, as matter attempts to gravitationally collapse, the energy density of that region rises above this average. But radiation responds to those higher energy densities by flowing out of those high-density regions into the lower density ones, and this leads to a sort of “bounce,” where:

• densities rise,
• photon pressure increases,
• photons flow out,
• the density drops,
• causing the photon pressure to drop,
• causing photons and matter to flow back in,
• increasing the density,

and the cycle continues. When we talk about the fluctuations we see in the cosmic microwave background, they follow a particular pattern of “wiggles” that corresponds to these “bounces,” or acoustic oscillations, occurring in the plasma of the early Universe.

But there’s a third thing happening concurrently with all of these: the Universe is expanding. When the Universe expands, its density drops, since the total number of particles within it stays the same while the volume increases. A second thing, however, happens as well: the wavelength of every photon — every quantum of electromagnetic radiation — stretches as the Universe expands. Because a photon’s wavelength determines its energy, with longer wavelengths corresponding to lower energies, the Universe also cools off as it expands.

A Universe that gets less dense and cools from an initially hot and dense state will do a lot more than just gravitate. At high energies, every collision between two quanta will have a chance to spontaneously create particle/antiparticle pairs; as long as there’s enough energy available in each collision to create massive particles (and antiparticles) via Einstein’s E = mc², there’s a chance it will happen.

At early times, this happens copiously, but as the Universe expands and cools, it stops happening, and instead when particle/antiparticle pairs meet, they annihilate away. When the energy drops to low enough values, only a tiny excess of matter will remain.

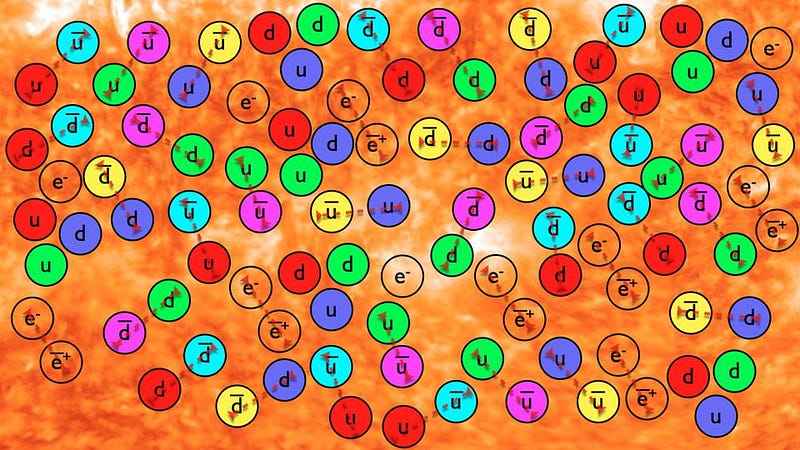
As the Universe continues to expand and cool — and as the density and temperature both drop — a number of other important transitions happen. In order:

• quarks and gluons form stable, bound states: protons and neutrons,
• neutrinos, which previously interacted copiously, no longer collide with other particles,
• the last of the antimatter pairs, electron and positrons, annihilate away,
• the photons cool off sufficiently so that the first stable nuclear fusion reactions occur, creating the light elements in the immediate aftermath of the Big Bang,
• the oscillating dance between normal matter, dark matter, and radiation takes place, leading to the particular pattern of fluctuations that will later grow into the Universe’s large-scale structure,
• and, finally, neutral atoms can stably form, as the photons have cooled enough that they no longer immediately blast electrons off of the nuclei they’d bind to.

It’s only until this final step is complete — a step taking over 100,000 years — that the Universe becomes transparent to the light present within it. The ionized plasma that existed previously absorbs and re-emits photons continuously, but once neutral atoms form, those photons simply free-stream and redshift with the expanding Universe, creating the cosmic microwave background we observe today.

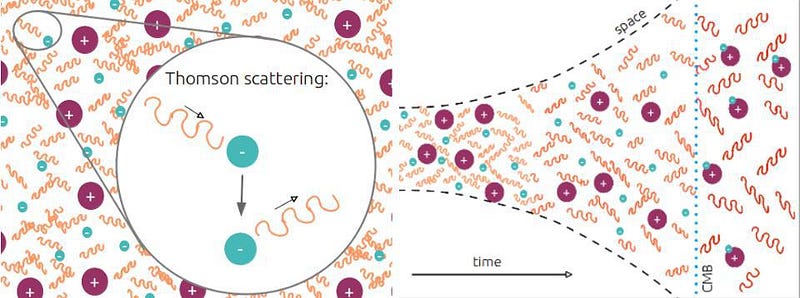
That light, on average, comes to us from a time corresponding to ~380,000 years after the Big Bang. This is incredibly short compared to our Universe’s history of 13.8 billion years, but is very long compared to the earlier steps, which occur over the first fraction-of-a-second to the first few minutes after the Big Bang. Because photons outnumber atoms by more than a billion-to-one, even a tiny number of super-energetic photons can keep the entire Universe ionized. Only when they cool to a specific threshold — corresponding to a temperature of about ~3000 K — can these neutral atoms finally form.

But there’s an immediate problem with that final step, if you think about it.

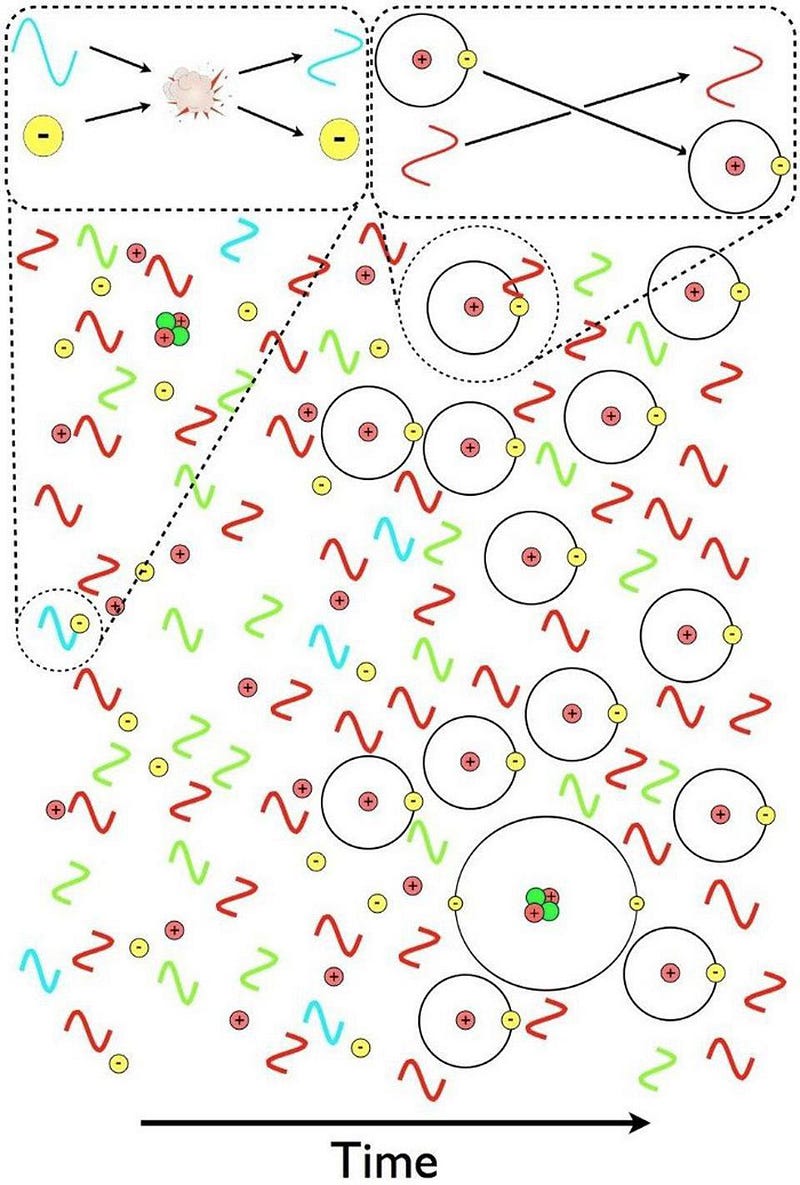
When electrons bind to atomic nuclei, they’ll cascade down the various energy levels in a chain reaction. Eventually, those electrons will make their most energetic transition: to the ground state. The most common transition that occurs is from the second-lowest energy state (called n=2) to the lowest state (n=1), in which case it emits an energetic, Lyman-series photon.

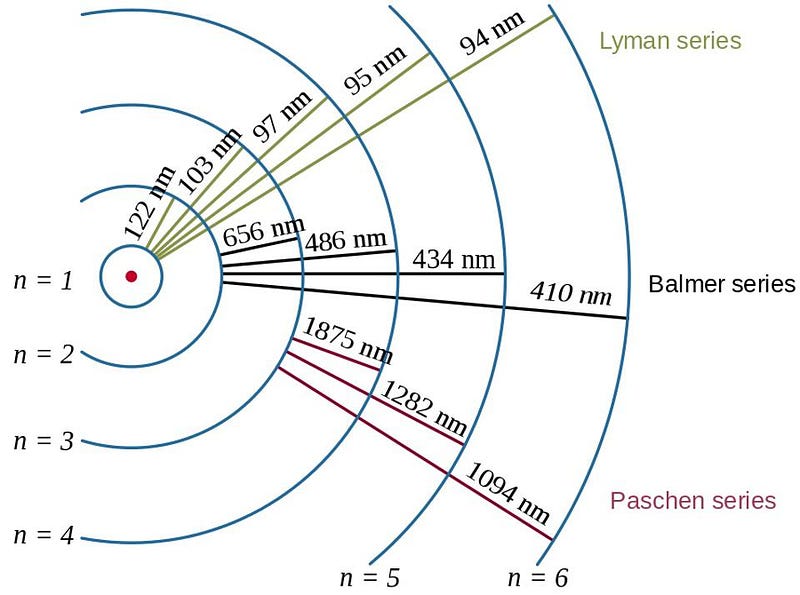
Why is this a problem? We needed the Universe to cool below about ~3000 K so that there wouldn’t be enough energetic photons to re-excite those ground-state electrons back to an excited state, where they’d be easy to ionize. So we waited and waited and waited, and finally, a few hundred thousand years after the Big Bang, we got there. At that time, electrons bind to nuclei, they cascade down their various energy levels, and finally make a transition down to a ground state.

That energetic, final transition causes the emission of a high-energy, Lyman-series photon. Now, if you’ve begun to form neutral atoms all over the Universe, you can calculate how far that Lyman-series photon travels before smashing into a neutral atom, and compare that to the amount of redshifting that will occur for that photon. If it redshifts by a great enough amount, its wavelength will lengthen and atoms won’t be able to absorb it. (Remember, atoms can only absorb photons of particular frequencies.)

When you do the math, however, you find that the overwhelming majority of photons produced by these transitions to the ground state — about 99,999,999 out of every 100,000,000 — simply get reabsorbed by another, identical atom, which then can very easily become ionized.

This implies something rather disturbing: we waited all this time for the Universe to become electrically neutral, and then when it does, we calculate that practically every atom that does so will itself be responsible for re-ionizing a different atom of the same type.

You might think that this means we just need to wait for a sufficient amount of time, and then enough of these transitions will occur with a sufficiently long time passing between when those photons are emitted and it encounters another atom. That’s true, but the time it would take for the Universe to become electrically neutral wouldn’t be ~380,000 years if this were the way it happened. Instead, it would take more like ~790,000 years for this transition to occur, where the Universe would have dropped all the way down to more like ~1900 K in temperature.

In other words, the simplest way you’d attempt to form neutral atoms — the way it happens naturally when the ions in our Universe recombine today — cannot be the main mechanism for how it occurred in the early Universe.

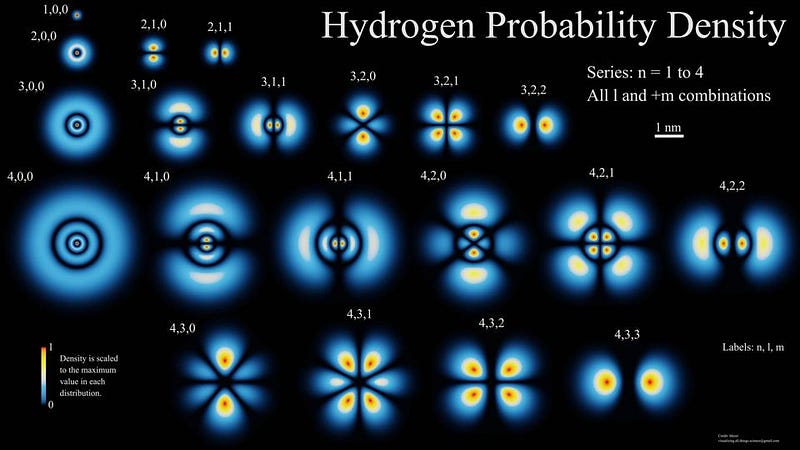
So how does it happen, then? You have to remember that the lowest-energy state for an electron in an atom, the n=1 state, is always spherical. You can fit up to two electrons in that state, and so hydrogen — the most common element in the Universe — always has one electron in the n=1 state when it gets there.

However, the n=2 state can fit up to eight electrons: there are two slots in a spherical state (the s-orbital) and two slots in each of the x, y, and z directions (the p-orbitals).

The problem is that transitions from one s-orbital to another are forbidden, quantum mechanically. There’s no way to emit one photon from an s-orbital and have your electron wind up in a lower energy s-orbital, so the transition we talked about earlier, where you emit a Lyman-series photon, can only occur from the 2p state to the 1s state.

But there is a special, rare process that can occur: a two-photon transition from the 2s state (or the 3s, or 4s, or even the 3d orbital) down to the ground (1s) state. It occurs only about 0.000001% as frequently as the Lyman-series transitions, but each occurrence nets us one new neutral hydrogen atom. This quantum mechanical quirk is the primary method of creating neutral hydrogen atoms in the Universe.

If it weren’t for this rare transition, from higher energy spherical orbitals to lower energy spherical orbitals, our Universe would look incredibly different in detail. We would have different numbers and magnitudes of acoustic peaks in the cosmic microwave background, and hence a different set of seed fluctuations for our Universe to build its large-scale structure out of. The ionization history of our Universe would be different; it would take longer for the first stars to form; and the light from the leftover glow of the Big Bang would only take us back to 790,000 years after the Big Bang, rather than the 380,000 years we get today.

In a very real sense, there are a myriad of ways that our view into the distant Universe — to the farthest reaches of deep space where we detect the earliest signals arising after the Big Bang — that would be fundamentally less powerful if not for this one quantum mechanical transition. If we want to understand how the Universe came to be the way it is today, even on cosmic scales, it’s remarkable how subtly dependent the outcomes are on the subatomic rules of quantum physics. Without it, the sights we see looking back across space and time would be far less rich and spectacular.

Starts With A Bang is written by Ethan Siegel, Ph.D., author of Beyond The Galaxy, and Treknology: The Science of Star Trek from Tricorders to Warp Drive.