How far away are the stars?

Out there in space, blazing just a scant 150 million kilometers away lies the brightest and most massive object in our Solar System: the Sun. Shining hundreds of thousands of times as bright in Earth’s skies as the next brightest object, the full Moon, the Sun is unique among Solar System objects for producing its own visible light, rather than only appearing illuminated because of reflected light. However, the thousands upon thousands of stars visible in the night sky are all also self-luminous, distinguishing themselves from the planets and other Solar System objects in that regard.

But how far away are they?

Unlike the planets, Sun, and Moon, the stars appear to remain fixed in their position over time: not only from night-to-night but also throughout the year and even from year-to-year. Compared to the objects in our own Solar System, the stars must be incredibly far away. Furthermore, in order to be seen from such a great distance, they must be incredibly bright.

It only makes sense to assume, as many did dating back to antiquity, that those stars must be Sun-like objects located at great distances from us. But how far away are they? It wasn’t until the 1600s that we got our first answers: one each from Robert Hooke, Christiaan Huygens, and Isaac Newton. Unsurprisingly, those early answers didn’t agree with one another, but who came closest to getting it correct? The story is as educational as it is fascinating.

The stars that are closest to Earth will appear to shift periodically with respect to the more distant stars as the Earth moves through space in orbit around the Sun. Before the heliocentric model was established, we weren’t looking for “shifts” with a ~300,000,000 kilometer baseline over the span of ~6 months, but rather a ~12,000 kilometer baseline over the span of one night: Earth’s diameter as it rotated on its axis. The distances to the stars are so great that it wasn’t until the 1830s that the first parallax, with a 300 million km baseline, was detected. Today, we’ve measured the parallax of over 1 billion stars with ESA’s Gaia mission.

The first method: Robert Hooke

The simplest, most straightforward and direct way to measure the distances to the stars is one that dates back thousands of years: the notion of stellar parallax. The idea is the same one as the phenomenon behind the game we all play as children, where you:

• close one eye,
• hold your thumb up at arm’s length from you,
• then switch which eye is closed and which one is open,
• and watch your thumb shift relative to the objects farther away in the background.

Whenever you have two different vantage points to look from (such as each of your two eyes), objects that are close by will appear to “shift” relative to the objects that are farther away. This phenomenon, known as parallax, could theoretically be used to measure the distances to the closest among the stars.

Assuming, that is, that they’re close enough to appear to shift, given the limitations of our bodies and our equipment. In ancient times, people assumed the Universe was geocentric, and so they attempted to observe parallax by looking at the same stars at dawn and at dusk, seeing if a baseline distance of Earth’s diameter between the two observing points would lead to an observable shift in any stars. (They do not.) But in the 1600s, after the work of Copernicus, Galileo, and Kepler, scientist Robert Hooke thought the method might now bear fruit.

This drawing shows Robert Hooke’s zenith telescope, constructed in the late 1660s and used to attempt to measure the position of the zenith star at his location, Gamma Draconis, and any variations in its position with respect to a plumb line, which would indicate a stellar parallax.

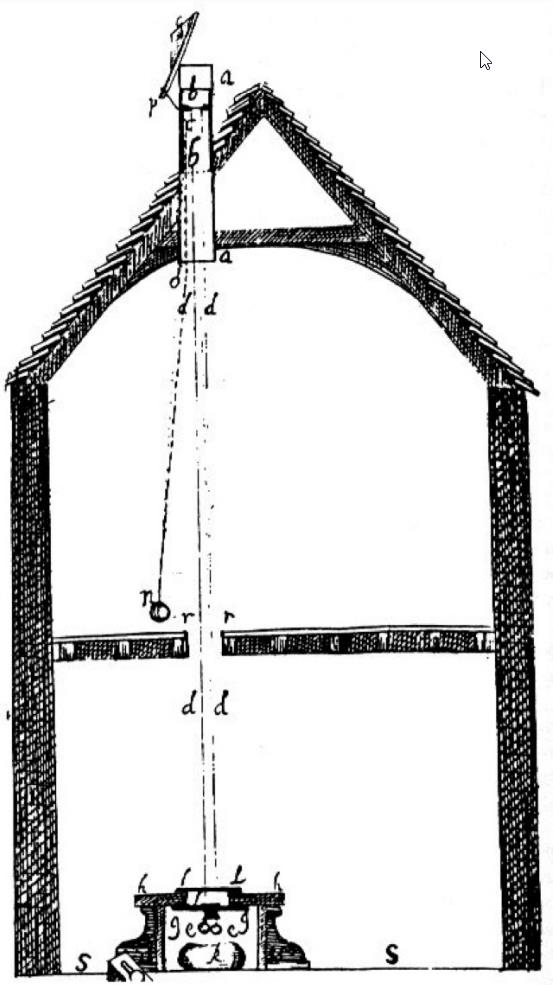
In the late 1660s, Hooke went for it. He knew that atmospheric refraction (or the bending of light rays due to Earth’s atmosphere) might be a problem, so to minimize that effect, he built what’s known as a zenith telescope: a telescope that looked straight up overhead, minimizing the amount of Earth’s atmosphere that light would need to travel through. Measuring the position of Gamma Draconis — the zenith star as visible from London, England — Hooke took multiple observations of the star over the course of the year, looking for any apparent shift in its position from “true zenith,” to the best precision his instruments could muster.

He recorded four measurements beginning in 1669, and noticed a variation that he claimed was observable with the precision of his instruments: 25 arc-seconds, or about 0.007 degrees. He published his results in An Attempt to Prove the Motions of Earth by Observations in 1674, wherein he wrote:

“Tis manifest then by the observations … that there is a sensible parallax of Earth’s Orb to the fixt Star in the head of Draco, and consequently a confirmation of the Copernican System against the Ptolomaick [Ptolemaic] and Tichonick [Tychonic].”

The inferred distance to Gamma Draconis, according to Hooke, works out to about 0.26 light-years, or 16,500 times the Earth-Sun distance.

The way that light spreads out as a function of distance means that the farther away from a power source you are, the energy that you intercept drops off as one over the distance squared. This also illustrates, if you view a certain specific angular area (illustrated by the squares) from the perspective of the original source, how larger objects at greater distances will appear to take up the same angular size in the sky. Each time you double your distance between a source and observer, the brightness you observe gets quartered. In general, photons (and all light) propagate spherically outward away from the emitting source.

The second method: Christiaan Huygens

Many astronomers, throughout the 17th century and even earlier, had an idea for how to estimate the distances to the stars:

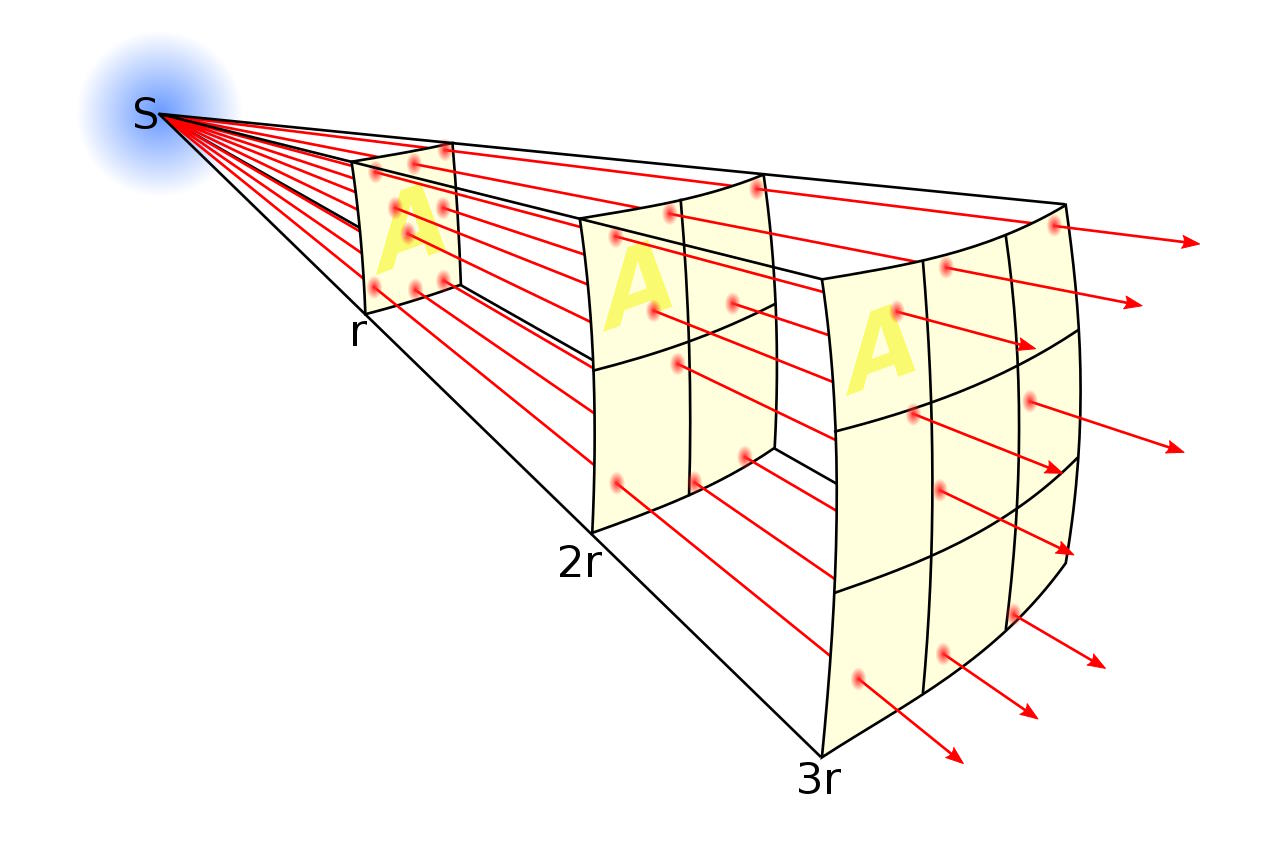
• assume that the Sun is a typical star, with a typical intrinsic brightness and size,
• measure the relative brightness of the Sun to a star,
• and then use the fact that brightness falls off as one-over-the-distance-squared (an inverse square law, as shown above) to calculate how much farther away the stars are than the Sun is.

The problem that they all faced, however, was the difficulty of that second step. Given that the Sun is so incredibly bright and the stars — even the brightest among them — are so incredibly faint, that a fair comparison seemed practically impossible.

That’s where Huygens came in. He began with a long, opaque, large-aperture tube, and viewed the brightest star in the night sky through it: Sirius. He then fastened a light-blocking brass disk over the edge of the tube, but drilled a number of holes in it: for use during the daytime. Huygens realized that if he could drill holes that were smaller and smaller, only allowing a tiny, minuscule fraction of the Sun’s light through, he would eventually create a hole so small that it would have the same brightness to his eyes as Sirius did the night before.

By holding up an opaque surface with a tiny hole poked in it, you can reduce the brightness of the Sun. However, even the tiniest hole one can create will still result in a much brighter “pinprick” of light than any star in the night sky will deliver to your eye: a problem that Christiaan Huygens had to reckon with in his 1698 attempt to estimate the distances to the stars.

Unfortunately for Huygens, even the smallest hole he was able to drill in his brass disk left him with a pinprick of light that was far, far brighter than any of the stars he saw. What he did, then, was to insert, into the smallest of the holes he drilled, tiny glass beads that would further fainten the sunlight that filtered through it, reducing its brightness by still greater amounts.

Compared to the full, unfiltered light from the Sun, Huygens calculated that he had to reduce its brightness by a factor of 765.3 million (765,300,000) in order to match the same brightness that Sirius would possess at night. Because brightness falls off as one over the distance squared, that means the square root of that number would tell him how much farther away the star in question (Sirius) would be as compared to the Earth-Sun distance: a factor of 27,664.

That works out to 0.44 light-years, or 27,664 times the Earth-Sun distance. It turns out that Sirius isn’t quite Sun-like, but intrinsically is about 25.4 times brighter than the Sun. If Huygens had known that fact, he would have computed the distance to be 2.2 light-years: somewhat closer to the actual distance of 8.6 light-years, which wasn’t bad for an estimate made back in 1698!

An illustration of the method of Gregory, later used by Newton, to estimate the distance to the stars based on the observed brightness of the planets, which themselves reflect sunlight.

The third method: Isaac Newton

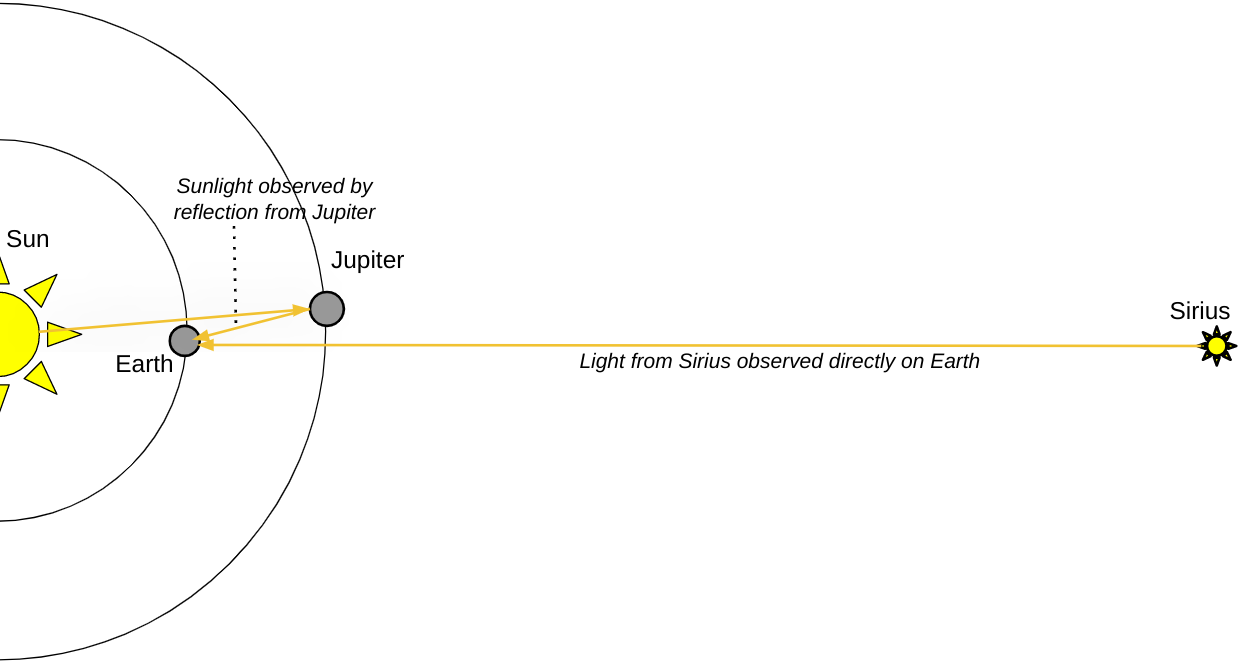
Way back in 1668, a contemporary and friend of Isaac Newton, James Gregory, wrote a treatise entitled Geometriae pars universalis, where he came up with an ingenious method that, quite arguably, was superior to Huygens’ method for measuring the relative brightness of the Sun to the stars: to use a planet as an intermediary. If you can find a planet in our Solar System whose brightness matches the brightness of a star precisely, and you observe that planet at that particular instant, then all you have to do is:

• calculate how far the light had to travel and “spread out” from the Sun before hitting the planet,
• know how much of the sunlight that strikes the planet gets reflected,
• know the diameter (i.e., physical size) of the planet he was observing, and
• then calculate how the reflected light from the planet spreads out before it reaches your eyes.

Gregory did a preliminary calculation himself, but warned that it would be untrustworthy until better estimates of Solar System distances were known.

Although Gregory (perhaps more famous, historically, for designing the Gregorian telescope) would die young (at the age of 36) in 1674, Newton possessed a copy of his book and was quite familiar with it, and worked out a more precise version of Gregory’s calculations, perhaps as early as 1685 by some estimations. It was only after Newton’s death in 1727, however, that his final manuscript was collected and published, seeing the light of day in 1728 under the title of The System of the World (De mundi systemate), even though it was originally intended to be the third volume of his much more famous Principia Mathematica.

This animation switches between a visible light (Hubble) view of Saturn and its main rings and the infrared (JWST) view of the same sight, albeit a little bit closer to Saturnian equinox. Both images are dominated by reflected light, where the different wavelengths highlight different features in Saturn’s atmosphere and rings. Although Newton knew the size of and distance to Saturn, he had no way of knowing its reflectivity.

The advantages to using Gregory’s methods were clear:

• you could observe Sirius and whatever planet you chose for comparison simultaneously, rather than having to rely on your memory from hours earlier to compare brightnesses,
• you could observe them under similar observing conditions,
• and, in the aftermath of Newton’s laws and with Newton’s reflecting telescope, it would be possible to both know the distance to the planets and also their physical size at that distance.

Although Gregory performed his initial estimates using Jupiter as a calibration point, Newton instantly recognized that Saturn, being the most distant known planet from the Sun at the time, would provide a better baseline. (Although Jupiter always appears brighter than Sirius and Saturn always appears fainter than Sirius.) Based on observations by John Flamsteed in 1672, Newton knew that Saturn was about 9-to-10 times farther away from the Sun than Earth, and was also about 10 times larger, in diameter, than Earth is.

What Newton didn’t know, however, was how reflective Saturn was (i.e., what its albedo was; he guessed it reflected 50% of the light that struck it), and he also didn’t know — just like Huygens — how intrinsically bright Sirius was (he assumed it was identical to the Sun). His answer was larger than that of either Huygens or Hooke: about 300,000 times the Earth-Sun distance, or in modern terms, about 4.7 light-years.

This image shows Sirius A and B, a bluer and brighter star than our Sun and a white dwarf star, respectively, as imaged by the Hubble space telescope. Sirius A, the main star, is an A class star (as opposed to our Sun being a G class star): twice as massive as the Sun, some ~4000 K hotter than the Sun at its photosphere, and about 25 times as intrinsically luminous as our Sun.

Evaluating the three methods

Three scientists; three methods; three different answers. But how far away were the stars, really?

Huygens’s and Newton’s methods, while very clever given the limited instrumental capabilities available to them during their lives, suffered from a big problem: you needed to know something intrinsic about the brightness of the stars you were observing relative to the Sun, which is information that astronomers would not possess until the 20th century. Whereas Huygens underestimated the distance to Sirius even after you account for its larger intrinsic brightness than the Sun, if you apply that same correction to Newton’s method, it turns out that he significantly overestimates the distance to Sirius; Gregory’s original, admittedly unreliable estimate (of 83,190 times the Earth-Sun distance, or 1.32 light-years) actually turned out to be better than Newton’s, because if you correct for the actual intrinsic brightness of Sirius, it yields a distance estimate of 6.6 light-years: a difference of just 23% from the true value!

Hooke, on the other hand, may have used the best method that still applies in our modern era, but grossly misinterpreted what he was observing. As science historian Thony Christie documents, scientist James Bradley went through a painstaking attempt to reproduce Hooke’s experiment using multiple high-precision telescopes constructed explicitly for this purpose in 1725, using both his own house and the house of Samuel Molyneaux, his neighbor, for independent verification. Again, they went to observe that same star that Hooke observed: Gamma Draconis.

When the observer of a distant object is in motion, their motion causes the apparent positions of objects to shift relative to their actual positions: a phenomenon predicted much later than it was observed by Einstein’s relativity and the Lorentz transformations. The phenomenon of this apparent shift is known as stellar aberration, and it was this effect, not stellar parallax, that accounted for the perceived motions of stars in the sky over the course of the year in the 1600s and 1700s.

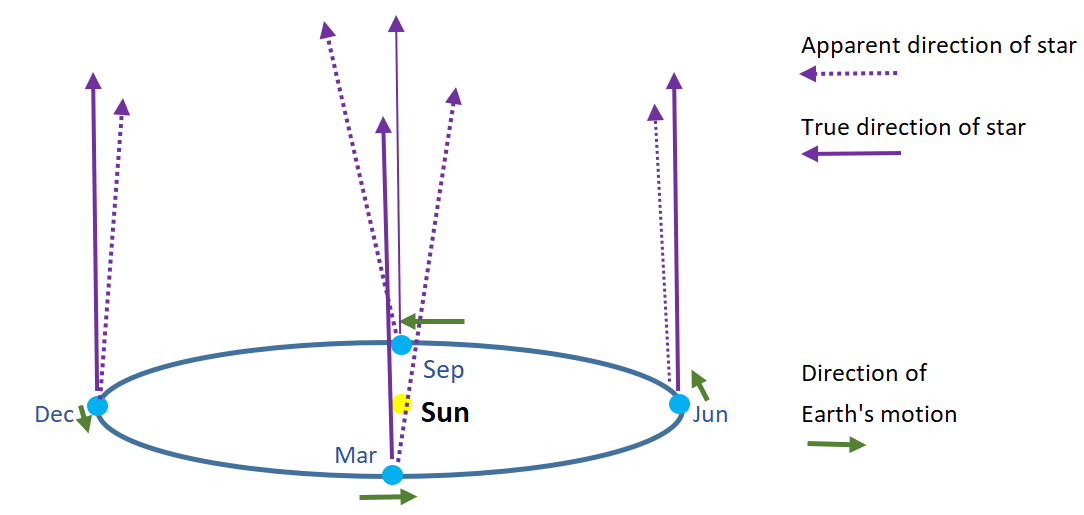
Fascinatingly, Bradley actually did observe that the star’s position was seen to change, albeit slightly, over the course of a year. In fact, the star traced out a tiny ellipse, which is the shape you might expect, since the Earth orbits around the Sun in an elliptical path: something that had been known since the time of Kepler in the early 1600s. But Bradley, careful as he was, noted that this couldn’t be due to stellar parallax for an important reason: the changes in position were in the wrong direction! As Christie writes,

“Bradley knew that this was not parallax because the changes in position were in the wrong directions, when according to the parallax theory the star should have moved south it moved north and vice versa. Bradley could not believe his own results and spent another year meticulously repeating his observations; the result was the same.”

What could be causing this motion? Unbeknownst to Bradley at the time, he had just discovered the phenomenon of stellar aberration: where celestial objects appear to shift position based on the motion of the observer. In the case of Gamma Draconis as seen from Earth, the motion of the observer is largely driven by the motion of the Earth around the Sun at a speed of around ~30 km/s, or about 0.01% the speed of light. Although it was sufficient to prove that Earth does, indeed, orbit around the Sun, it was no detection of parallax at all.

61 Cygni was the first star to have its parallax measured and published (back in 1838), but also is a difficult case due to its large proper motion. These two images, stacked in red and blue and taken almost exactly one year apart, show this binary star system’s fantastic speed. If you want to measure the parallax of an object to extreme accuracy, you’ll make your two ‘binocular’ measurements simultaneously, to avoid the effect of the star’s motion through the galaxy. Gaia is exceptionally good at characterizing the orbits of nearby stars with small separations from their companion, but faces more challenges with more distant, wider binary systems.

Parallax wouldn’t be detected until the 1830s, when three separate astronomers — Thomas Henderson, Friedrich Bessel, and Wilhelm Struve — looking at three different stars (Alpha Centauri, 61 Cygni, and Vega, respectively) all detected an actual motion throughout the year, definitively measuring stellar parallax. Although Henderson made his observations first, in 1833, he didn’t publish his results until 1839. Meanwhile, Struve had preliminary but unreliable data about Vega that he published in 1837, and wouldn’t publish a superior measurement until 1840. Meanwhile, Bessel published his high-quality data in 1838, and is generally regarded as the discoverer of the first stellar parallax.

The true game-changing invention would be the development of photography as applied to astronomy, which led to the first photographs of the Moon and Sun in the 1840s and, eventually, the first photograph of a star in 1850. Being able to compare photographs, initially by eye and now in a computerized fashion, has led to the modern measurement of more than a billion stellar parallaxes with the European Space Agency’s Gaia satellite. Parallax, not brightness measurements, are the way to actually measure the distance to the stars.

Of the three early estimates made, however, Hooke’s claimed “parallax” distance was by far the worst. While Huygens and Newton were within an order of magnitude of the correct answer (once one corrects for intrinsic stellar brightness), Hooke’s measurements were off by more than a factor of 1000! The star Gamma Draconis, despite being relatively bright, is actually quite far away: at over 150 light-years distant, its parallax was not detected until the Hipparcos Catalogue was published in 1997. Although, as humans, we tend to value getting the right answer regardless of the method used, in science, it’s the procedure that one follows — and the reproducibility of the answer — that truly matters.