Einstein Wins Again! General Relativity Passes Its First Extragalactic Test

The result validate Einstein on a whole new scale, and pose serious problems for alternative, modified theories of gravity.
In 1915, Albert Einstein put forth a new theory of gravity: General Relativity. Instead of every mass in the Universe instantly reaching across to every other mass and exerting an attractive force, the new concept of a cosmic fabric — spacetime — would curve in response to matter and energy. As the matter and energy moved through this spacetime fabric, the fabric would curve in response: not infinitely fast, but at the speed of light. And the matter and energy, moving through this curved space, would be told how to move by the fabric of space itself.
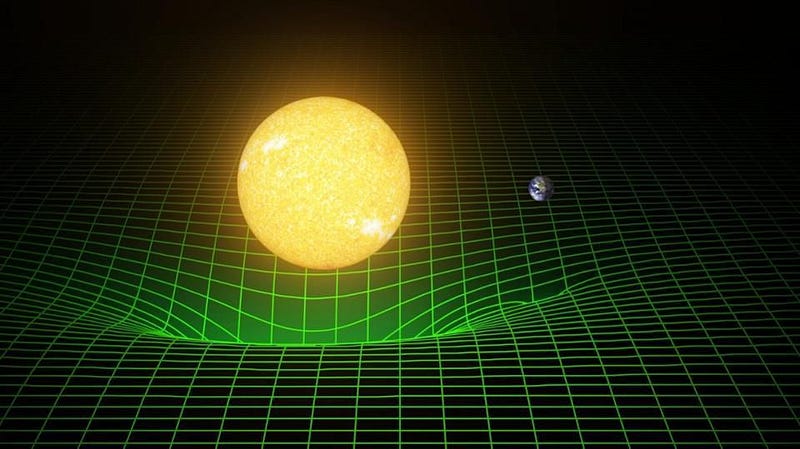
This revolutionary picture has been put to the test on Earth, in space, and wherever we’re able to look. Yet the only place we’ve ever sent missions capable of performing these tests are in our own Solar System; every test beyond requires a set of assumptions. Despite all our measurements of galaxies, clusters, gravitational lensing, and the large-scale structure of the Universe, we’ve never been able to directly test General Relativity, unambiguously, on scales beyond the Solar System.
There have been too many confounding variables, like dark matter, to know whether General Relativity is right and dark matter is truly real. Until we can perform an unambiguous, direct test of General Relativity on galactic-or-larger scales, modified gravity alternatives will be impossible to rule out.
In order to test General Relativity as a theory of gravity, you need to find a system where the signal you’ll see differs from other theories of gravity. This must at least include Newton’s theory, but should, ideally, include alternative theories of gravity that make distinct predictions from Einstein’s. Classically, the first such test that did this was right at the edge of the Sun: where gravity is strongest in our Solar System.
As light from a distant star passes close to the limb of the Sun, it should bend by a very specific amount, as dictated by Einstein’s theory. The amount is twice that of Newton’s theory, and was verified during the total solar eclipse of 1919. Since then, a number of additional tests have been performed to great precision. Each and every time, Einstein’s theory has been validated, and alternatives emerge defeated. Yet on scales larger than the Solar System, the results have always been inconclusive.

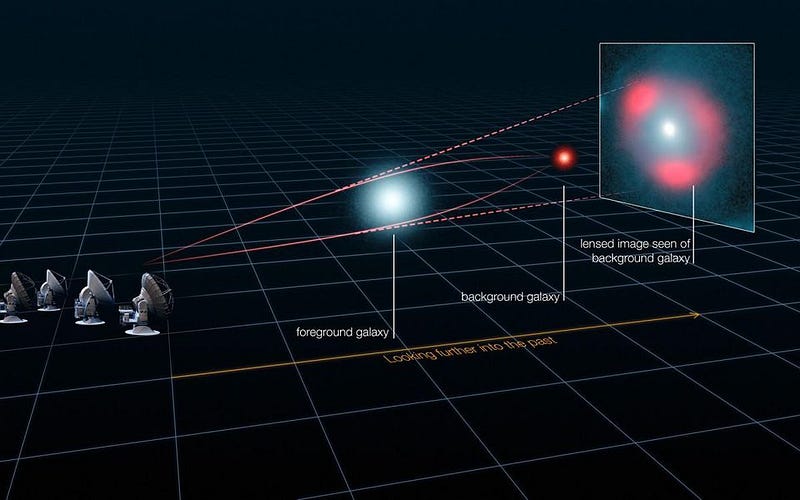
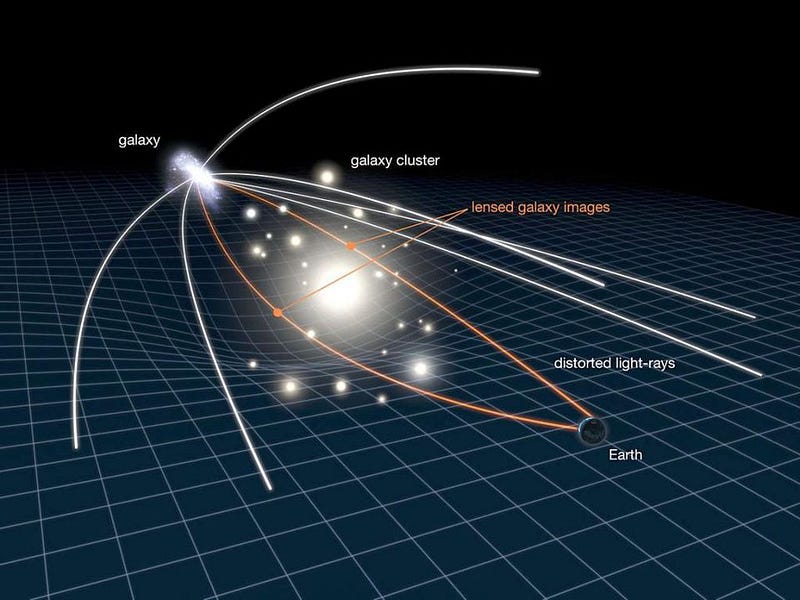
Until today. We’ve finally taken that first step towards verifying General Relativity on those large, cosmic scales, where gravity is often the only force that matters. Every galaxy or galaxy cluster in the Universe, owing to gravity, distorts the space it occupies. As a result, the light from background sources, relative to our line-of-sight, gets:
- stretched,
- distorted,
- magnified,
- and can appear in multiple images.
This effect of gravitational lensing, which occurs in both strong and weak variants, represents the greatest hope we have of testing General Relativity on scales larger than the Solar System. For the first time, a team of scientists led by Tom Collett performed a precise extragalactic test of General Relativity, and Einstein’s theory passed with flying colors.

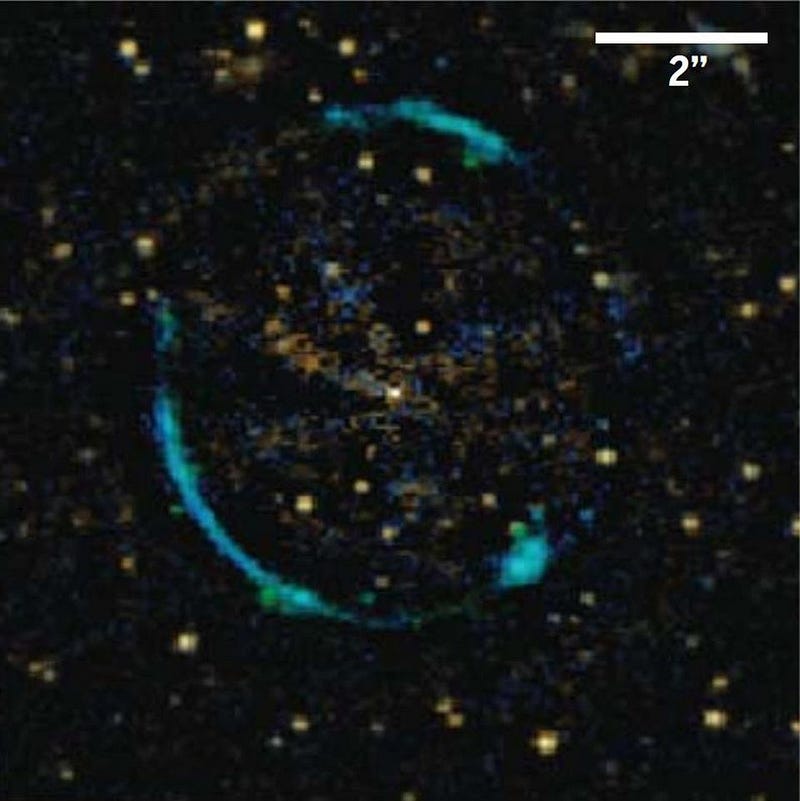
If you wanted an ideal laboratory, you’d pick a single, massive galaxy that acted like a strong lens. The galaxy would be relatively close by, so that we could both resolve the mass distribution (and individual stellar motions) inside of it. Additionally, a nearby galaxy would be relatively unaffected by the expansion of the Universe. And finally, it would exhibit the characteristic arcs and multiple images characteristic of strong lensing. In their paper, the team of Collett et al., using the Hubble Space Telescope, found a galaxy that met all of these criteria: ESO 325-G004, known as E325 for short.
As you can see, the galaxy contains a beautiful Einstein Ring, one of the surefire signatures of a strong lensing signal.

The lens itself is close by, at a meager distance of only 500 million light years. The background galaxy that gets stretched into a ring, however, has been traveling for more than 10 billion years before reaching our eyes. The fact that the lens is so close allows us to, with an observatory like Hubble or a large ground-based telescope, resolve measurements of the average motions of the stars in regions about 400 light years wide inside of it. With those measurements, we can place extremely tight constraints on how the mass is distributed in 3D inside E325.
Furthermore, because the ring appears in the inner portion of the galaxy, dark matter is unimportant; the normal matter dominates at this small radius. And to top it all off, there are extended arcs seen in E325, allowing us to constrain the mass profile of the lens. In other words, it’s the perfect laboratory for testing the validity of General Relativity on the scale of an individual galaxy.
The way you perform the test is to compare two different potentials that appear in the metric of spacetime: the Newtonian gravitational potential and the curvature potential. In General Relativity, these two potentials are equal, so their ratio, known as γ, is equal to 1. In many alternative theories, however, the ratio of the two potentials is scale-dependent, so we’d expect to observe something different from γ = 1. Pretty much every no-dark-energy model of the Universe (along with a number of models with no-dark-matter) has a ratio that’s different from γ = 1.
So if we can measure this parameter from a single galaxy, like E325, we’ll have our first robust measurement of whether General Relativity, on scales larger than the Solar System, is favored or disfavored.
The Very Large Telescope, part of the European Southern Observatory, has an instrument on it called MUSE, for the Multi Unit Spectroscopic Explorer. MUSE can obtain spatially resolved spectroscopic data across the lens, where light is broken up into individual wavelengths and analyzed. From that information, you can extract how quickly the stars are moving relative to one another on scales down to just 100 parsecs, which is 20 times as fine as the size of the Einstein ring.
From all of the MUSE and Hubble data, they can not only reconstruct the dynamical mass of the galaxy E325, they can make a best-fit model of a variety of properties of the galaxy. This includes a mass-to-light ratio for the stars, a dark matter halo, and a central, supermassive black hole. All told, once they understand the other parameters, they can compare the rest of the data to get a best-fit value for γ, and see whether it’s equal to 1, like General Relativity predicts, or different.
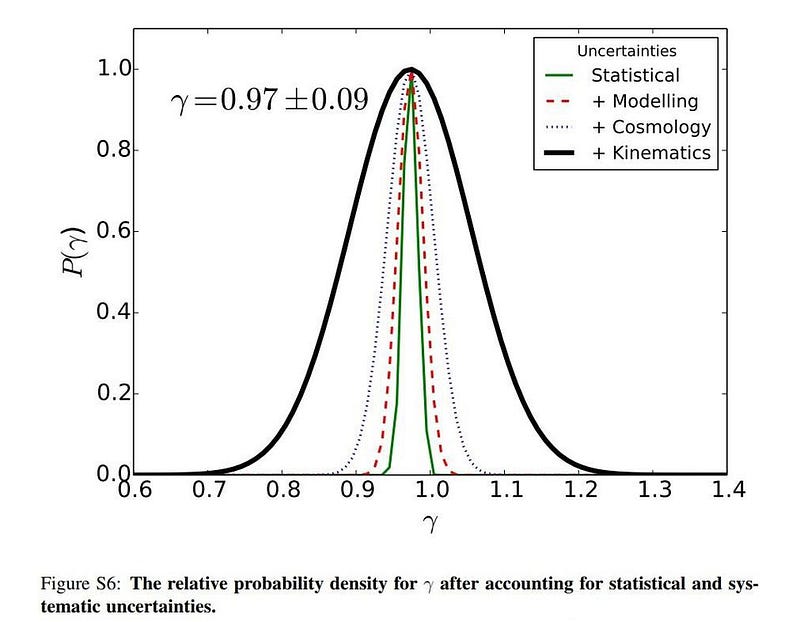
So what is the big find? Their best fit gives a value of γ = 0.978, with a statistical uncertainty (95% confidence) of ±0.03. Instead of scales of a tiny fraction of a light year, like we get in the Solar System, this test extends the validity of General Relativity out to an unprecedentedly large scale: nearly 7,000 light years. Even when they include all the possible systematic uncertainties, which are dominated by the speeds of the stellar motions which they base their dynamical model on, they conclude that γ = 0.97 ± 0.09. Within the conceivable uncertainties, General Relativity has been confirmed.

For the first time, we’ve been able to perform a direct test of General Relativity outside of our Solar System and get solid, informative results. The ratio of the Newtonian potential to the curvature potential, which relativity demands be equal to one but where alternatives differ, confirms what General Relativity predicts. Large deviations from Einstein’s gravity, therefore, cannot happen on scales smaller than a few thousand light years, or for masses the scale of an individual galaxy. If you want to explain the accelerated expansion of the Universe, you can’t simply say you don’t like dark energy and throw Einstein’s gravity away. For the first time, if we want to modify Einstein’s gravity on galactic-or-larger scales, we have an important constraint to reckon with.
Ethan Siegel is the author of Beyond the Galaxy and Treknology. You can pre-order his third book, currently in development: the Encyclopaedia Cosmologica.