Don’t trust your theoretical “proof”
Theorems are gold in math. But in physics? The Universe will surprise you.
“What we need is more people who specialize in the impossible.”
–Theodore Roethke
Physics is one of the most interesting sciences out there. It begins from a very simple postulate: that there are physical rules that nature plays by, and that by investigating the phenomena of the Universe itself, we can determine what those rules are. Even more powerfully, we can then use those rules to predict — if we learn the initial physical conditions of any system — what’s going to happen to it in the future.

This has led to some spectacular predictions over the history of humanity, from eclipses to the returns of comets to the transits of the planets.
But there’s an often-overlooked corollary that comes along with this idea: when we put forth overarching theories that describe our reality, they come along with mathematical, quantitative descriptions. In science — and in physics in particular — it isn’t enough to simply say what’s going to happen, we want to know how it’s going to happen, and by how much. This is true for every branch of fundamental physics, from gravitation to the behavior of light and charged particles to the nuclear forces that hold our atomic nuclei together.
We can take these mathematical descriptions — the ones that underlie our best and most successful models of reality — and see what their consequences are. One of the most surprising things about physics is that we can use what is known to infer the “rules” that govern the system, and then use those rules to derive new predictions.
That’s the essence of theory in science, and it leads to some of the most amazing consequences. But one of the things it leads to — if you accept the theory — is to a proof, or a theorem, of something that must inevitably happen.
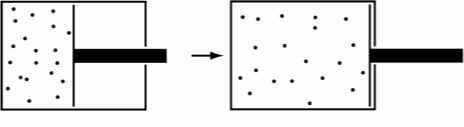
For example, take a system where there are many particles of say, air, where they’re all on one side of the room and there’s only a vacuum on the other, separated by a divider. Then, remove the divider. You’ll imagine that the particles will all mix together, and you’ll never get the original distribution — where all the particles are on one side and not the other — again.
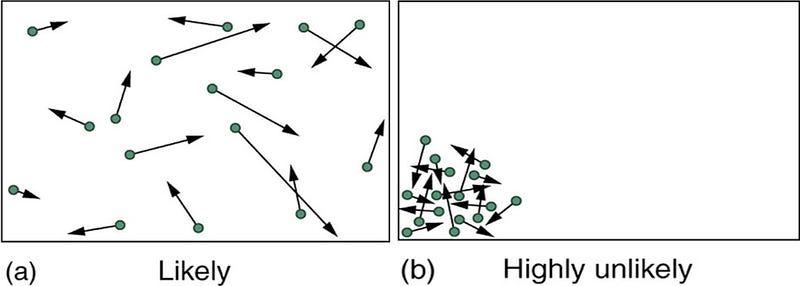
But there’s a proof that you will get that situation again: the Poincare recurrence theorem. It is scientifically provable that any closed system will return to any configuration that it enjoyed at any time, no matter how unlikely it is. In fact, it will return to that state an infinite number of times! This proof drove Boltzmann nuts, who quipped, at a demonstration of this proof, “you should live so long.”
What’s funny about this is that one can compute the time necessary for the Poincare recurrence to happen, and you get something like 10^10^100 years, or around a googleplex times the age of the Universe. Furthermore, if the system is anything other than perfectly close, the recurrence never occurs.
There are plenty other examples of “theorems” like this.
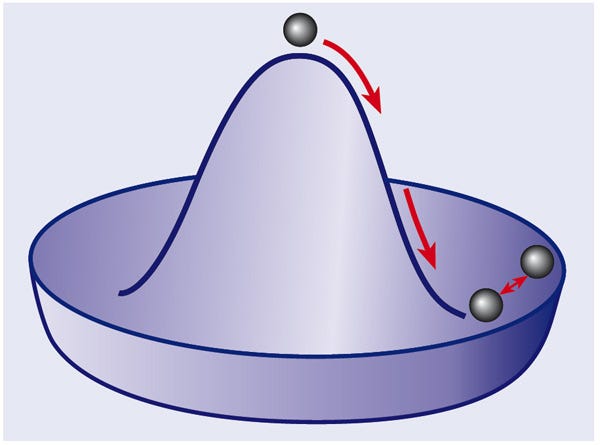
If you break a fundamental symmetry in physics, you should get a massless particle (or set of particles) out of it. (This is Goldstone’s theorem.) When you break the electroweak symmetry into the electromagnetic and weak forces (separately), you should get a set of massless particles out. Unfortunately, you wind up getting four particles out: the photon, the W+, the W- and the Z. While the photon is massless, the Z and W bosons are the third and fourth heaviest particles in the entire Universe! (#1 is the top quark; #2 is the Higgs boson.)
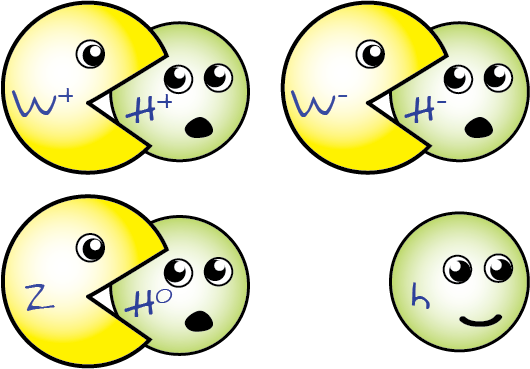
So why aren’t they massless? As it turns out, there is another aspect at play — that of the Higgs — that gives these three particles the heavy masses we observe. So it isn’t that the theorem is totally worthless or invalid, it’s simply that there’s a more subtle effect at play that significantly alters the scientific conclusion one would reach.
But while we can often predict the naive theorem, these subtle effects are far more difficult to predict. And if we only have the naive theorem, we can often be led to the entirely wrong conclusion.

Fast forward to today, and one of the interesting things to argue over is the ultimate origin of the Universe. Did the Universe — space and time — always exist? Did it have a beginning? Or is it a cyclical state?
We have a theorem — the Borde-Guth-Vilenkin theorem — that shows that inflationary spacetimes are not past-timelike-complete, meaning that although the hot Big Bang is indeed distinct and later from whatever or whenever the origin of the Universe was, the inflationary state that gave rise to it is probably not the full story.
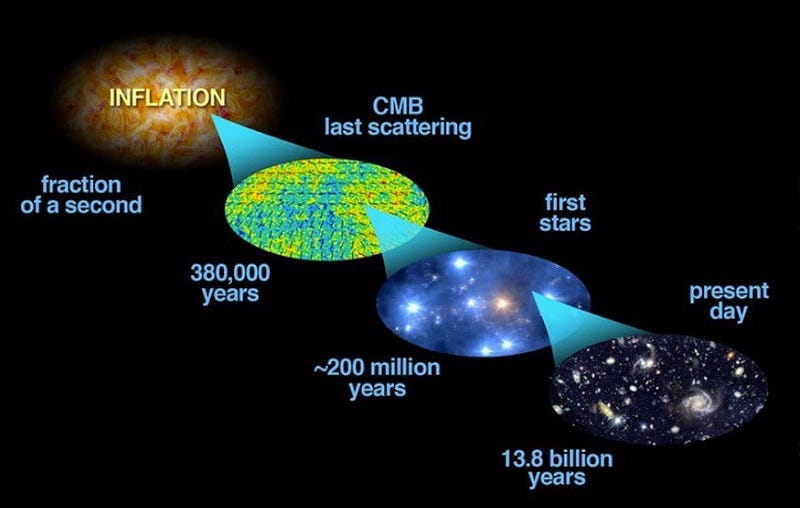
But does that necessarily mean that the inflationary state came from a singularity? Or that the existence of this theorem proves that the Universe had a finite extent backwards in time?
Not at all. That’s a derivable prediction of our best models of physical reality today, and if:
- they’re completely correct,
- there are no other mixing or altering effects,
- there’s no pre-inflationary state that leads to a different conclusion, and
- there are no loopholes in the theorem of which we aren’t aware,
then that’s the conclusion we’ll draw.
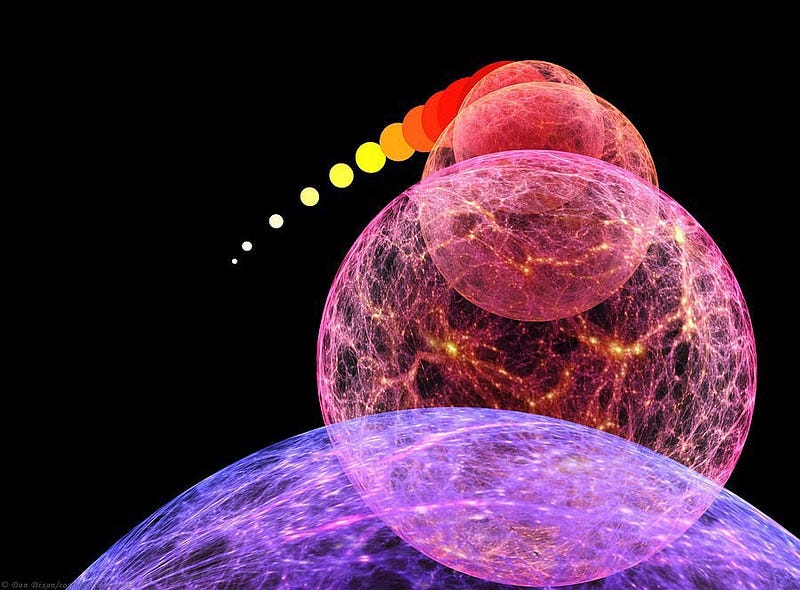
But for right now? We can definitely say that this theoretical “theorem” offers a compelling possibility: that the inflationary state did originate from a singularity. But theorem in physics is not as immutable as a mathematical theorem; there are plenty of loopholes that could arise, simply from the existence of physics that we don’t fully understand. (And there’s plenty that we don’t fully understand.)
So when you’re thinking about theoretical physics, and someone brings up a theorem that something must happen (or cannot happen) a certain way, keep in mind that — unlike math — the physics that underlies that theorem isn’t necessarily the whole story of the Universe. There are plenty of subtle effects, however small and insignificant they might seem, that can lead you to a completely different, or even the exact opposite conclusion from what your theorem supposedly “proved.”
The Universe is full of possibilities, and while our best theories can provide us with hints and tantalizing promises, it’s up to data — experiments and observations — to determine how our Universe actually is.
Leave your comments at the Starts With A Bang forum on Scienceblogs!





