How low-mass black holes bend space the most

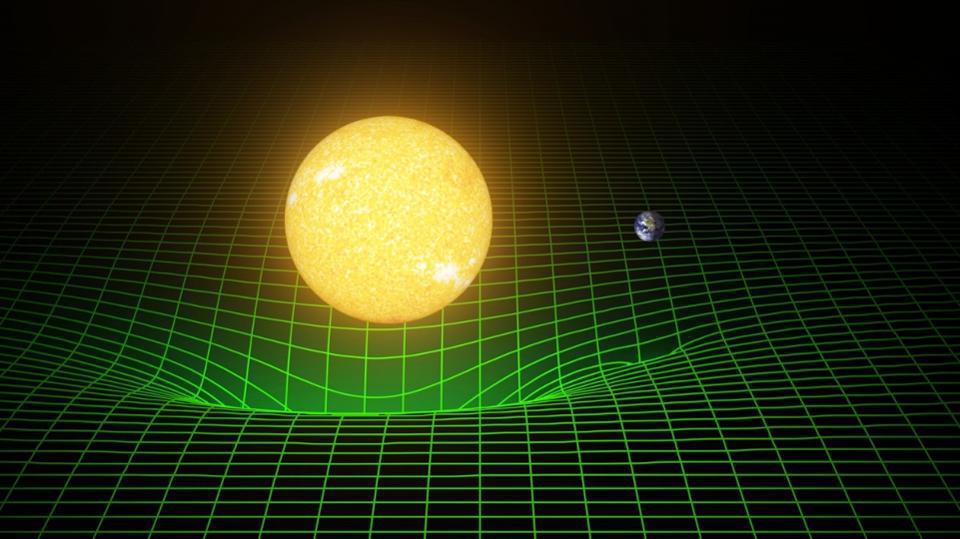
One of the most mind-bending concepts about the Universe itself is that gravity isn’t due to some unseen, invisible force, but comes about because the matter and energy in the Universe bends and distorts the very fabric of space itself. Matter and energy tell space how to curve, and that curved space lays out the path upon which matter and energy move. The distance between two points isn’t a straight line, but a curve determined by the fabric of space itself.

So where would you go if you wanted to find the regions of space that had the greatest amount of curvature? You’d pick the locations where you had the most mass concentrated into the smallest volumes: black holes. But not all black holes are created equal. Paradoxically, it’s the smallest, lowest-mass black holes that create the most severely curved space of all. Here’s the surprising science behind why.

During a total eclipse, stars would appear to be in a different position than their actual locations, due to the bending of light from an intervening mass: the Sun. The magnitude of the deflection would be determined by the strength of the gravitational effects at the locations in space through which the light rays passed.

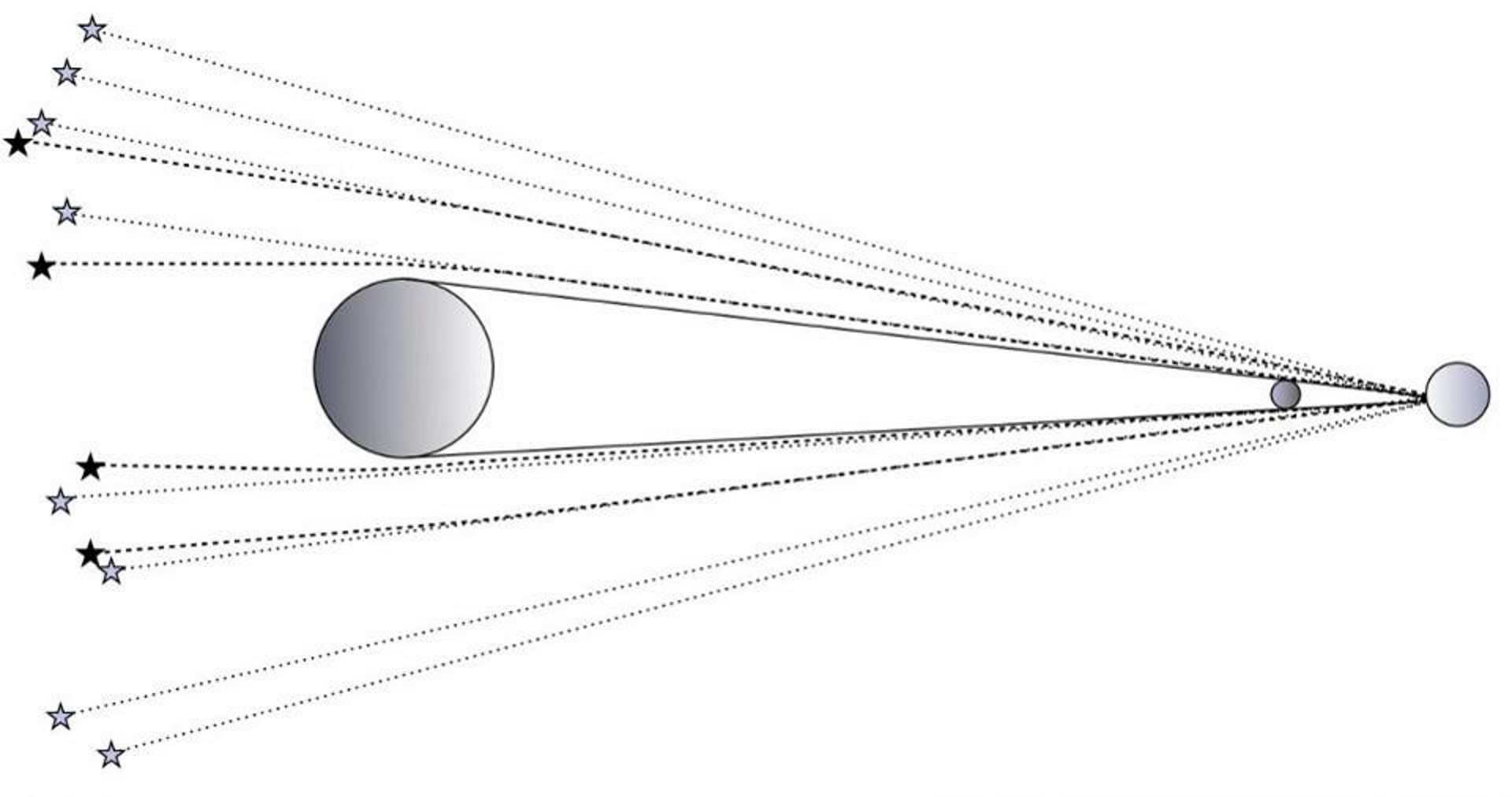
When we look out at the Universe, particularly on large cosmic scales, it behaves as though space were virtually indistinguishable from flat. Masses curve space, and that curved space deflects light, but the amount of deflection is minuscule even for the most concentrated amounts of mass we know of.

The solar eclipse of 1919, where the light from distant stars was deflected by the Sun, caused the path of light to bend by less than a thousandth-of-a-degree. This was the first observational confirmation of General Relativity, caused by the largest mass in our Solar System.

Gravitational lensing goes a step beyond that, where a very large mass (like a quasar or galaxy cluster) bends space so severely that the background light gets distorted, magnified, and stretched into multiple images. Yet even trillions of solar masses cause effects on scales of tiny fractions-of-a-degree.

An illustration of gravitational lensing showcases how background galaxies — or any light path — is distorted by the presence of an intervening mass, but it also shows how space itself is bent and distorted by the presence of the foreground mass itself. When multiple background objects are aligned with the same foreground lens, multiple sets of multiple images can be seen by a properly-aligned observer, or even an “Einstein ring” in the case of perfect alignment. If a transient event, like a supernova, occurs in the background galaxy, it will appear with time delays in the various images.

But it’s neither our proximity to a mass nor the total amount of mass that determines how severely space is curved. Rather, it’s the total amount of mass that’s present within a given volume of space. The best way to visualize this is to think about our Sun: a 1 solar-mass object with a radius of about 700,000 kilometers. At the very limb of the Sun, 700,000 km from its center, light deflects by about 0.0005 degrees.

• You could compress the Sun into about the size of Earth (similar to a white dwarf): about 6,400 km in radius. Light grazing this object’s limb would deflect by about 100 times as much: 0.05 degrees.
• You could compress the Sun into about a ~35 km radius (similar to a neutron star). Light grazing its limb would deflect a lot: by about a dozen degrees.
• Or you could compress the Sun so much it becomes a black hole: with a radius of about 3 km. Light grazing its limb would be swallowed, while light just outside it could deflect by 180° or even more.

Once you cross the threshold to form a black hole, everything inside the event horizon crunches down to a singularity that is, at most, one-dimensional. No 3D structures can survive intact. That’s the conventional wisdom, and has been treated as proven for over 50 years. But with rotation added into the mix, one of the assumptions of the “proof” seems to fall apart.

But there’s something important to think about in all of these scenarios. The total amount of mass — whether you have a Sun-like star, a white dwarf, a neutron star, or a black hole — is the same in each problem. The reason that space is more severely curved is because the mass is more concentrated, and you’re able to approach it much more closely.

If you instead stayed at the same distance from the center-of-mass in each scenario, 700,000 km away from a 1 solar mass object regardless of how compact it was, you’d see the exact same deflection: about 0.0005 degrees. It’s only because we can get very close to the most compact masses of all, i.e., black holes, that light deflects by such a severe amount as it grazes its limb.

This is a universal property of all black holes. When light just barely grazes the outside of the event horizon, it’s right on the border of getting swallowed, and it will maximally be bent around the outskirts of the black hole.

This artist’s impression depicts the paths of photons in the vicinity of a black hole. The gravitational bending and capture of light by the event horizon is the cause of the shadow captured by the Event Horizon Telescope. The photons that aren’t captured create a characteristic sphere, and that helps us confirm General Relativity’s validity in this newly-tested regime.

But not all black holes are created equal. Sure, there are some metrics by which every black hole looks the same, and those are important. Every black hole has an event horizon, and that horizon is defined by the location where the speed you’d need to travel in order to escape from its gravitational pull exceeds the speed of light. From outside the horizon, light can still make it to locations in the outside Universe; inside the horizon, that light (or any particle) gets swallowed by the black hole.

But the more massive your black hole is, the larger in radius its event horizon is. Double the mass and the radius of the event horizon doubles. Sure, lots of things will scale the same way:

• the escape velocity at the horizon is still the speed of light,
• the amount of light deflection follows the same mass-and-radius relationship,
• and — if we could image them all directly — they’d all exhibit that same donut-like shape we saw from the Event Horizon Telescope’s first image.

The features of the event horizon itself, silhouetted against the backdrop of the radio emissions from behind it, are revealed by the Event Horizon Telescope in a galaxy some 60 million light-years away. The dotted line represents the edge of the photon sphere, while the event horizon itself is interior even to that.

But there are a few properties that aren’t comparable for black holes of different masses. Tidal forces, for example, are a case where the differences are enormous. If you were to fall toward the event horizon of a black hole, you’d experience forces that would attempt to tear you apart by stretching you in the direction of the black hole’s center while simultaneously compressing you in the perpendicular direction: spaghettification.

If you fell into the black hole at the center of the galaxy M87 (the one imaged by the Event Horizon Telescope), the difference between the force on your head and the force on your toes would be tiny, less than 0.1% of the force of Earth’s gravity. But if you fell into a black hole with the mass of the Sun, the force would be many quintillions of times as great: enough to tear your individual atoms apart.

When two objects of a finite size gravitationally attract one another, the gravitational force on different parts of the object are different from the average value. This effect causes what we see and experience as tidal forces, which can get extremely large at short distances. Jupiter’s moon Io, with a large physical size but located very close to our Solar System’s most massive planet, Jupiter, experiences the largest tidal forces in the Solar System: some 10,000 times stronger than Earth experiences due to our Moon and Sun combined.

Perhaps the most striking difference between black holes of different masses, however, comes about from a phenomenon we’ve never actually observed: Hawking radiation. Wherever you have a black hole, you have a very small amount of low-energy radiation being emitted from it.

Although we’ve concocted some very pretty visualizations of what causes it — we typically talk about the spontaneous creation of particle-antiparticle pairs where one falls into the black hole and one escapes — that’s not what’s really going on. It is true that radiation is escaping from the black hole, and it’s also true that the energy from that radiation has to come from the mass of the black hole itself. But this naive picture of particle-antiparticle pairs popping into existence and one member escaping is grossly oversimplified.

The most common, and incorrect, explanation for how Hawking radiation arises is an analogy with particle-antiparticle pairs. If one member with negative energy falls into the black hole’s event horizon, while the other member with positive energy escapes, the black hole loses mass and outgoing radiation departs the black hole. This explanation has misinformed generations of physicists and came from Hawking himself. One of the errors inherent to this explanation is the notion that all of the Hawking radiation arises from the event horizon itself: it does not.

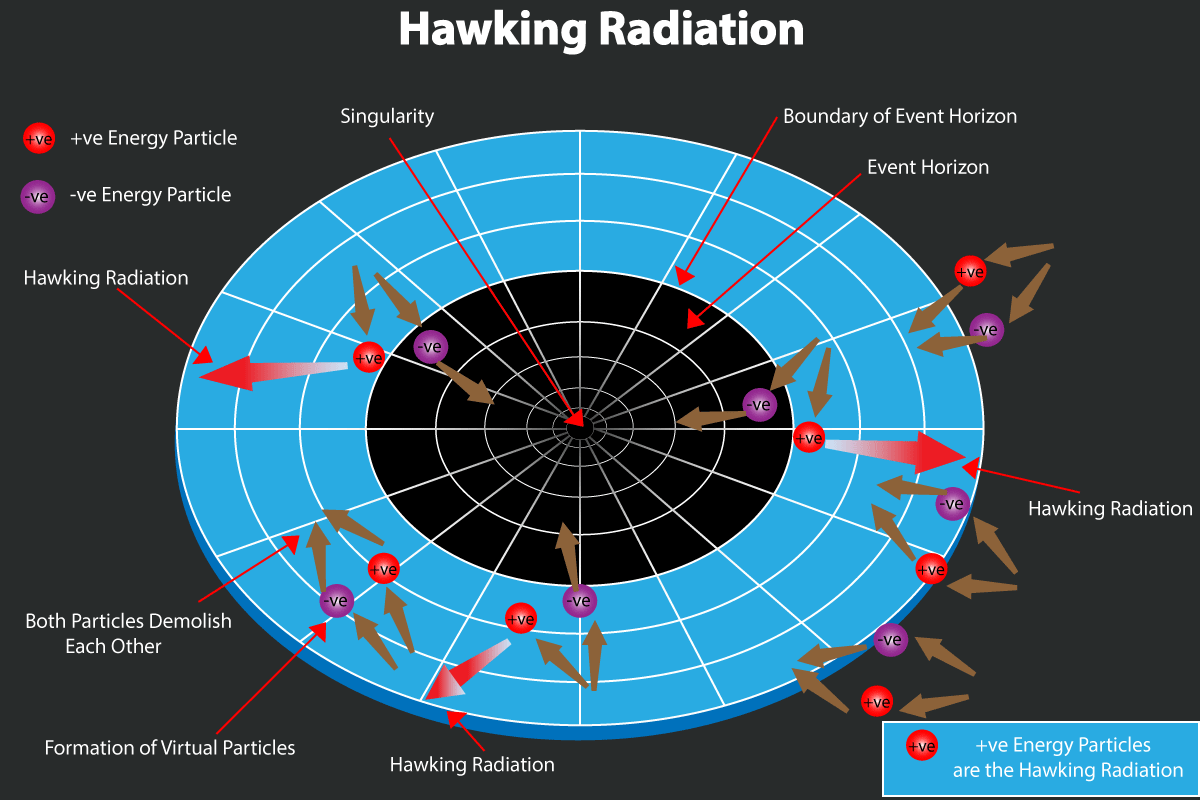
The real story is a little more complicated, but vastly more illuminating. Wherever you have space itself, you also have the laws of physics that exist in our Universe, which includes all the quantum fields that underlie reality. These fields all exist in their lowest-energy state when they permeate empty space, a state known as “the quantum vacuum.”

The quantum vacuum is the same for everyone so long as they’re in empty, uncurved space. But that lowest-energy state is different in places where the spatial curvature is different, and that’s where Hawking Radiation actually comes from: from the physics of quantum field theory in curved space. Far enough away from anything, even a black hole, the quantum vacuum looks like it does in flat space. But the quantum vacuum differs in curved space, and differs more dramatically where space is more severely curved.

Visualization of a quantum field theory calculation showing virtual particles in the quantum vacuum. (Specifically, for the strong interactions.) Even in empty space, this vacuum energy is non-zero. If there are additional particles or fields beyond what the Standard Model predicts, they will affect the quantum vacuum and will change the properties of many quantities away from their Standard Model predictions. However, the QCD contribution cannot be calculated perturbatively, the way electromagnetism can.

That means, if we want the brightest, most luminous, most energetic Hawking radiation to come from our black hole, we’d want to go to the lowest-mass black holes we can find: the ones where the spatial curvature at their event horizon is the strongest. If we were to compare a black hole like the one at the center of M87 with the imaginary one we’d have if the Sun became a black hole, we’d find:

• the more massive black hole has a temperature that’s billions of times lower,
• has a luminosity that’s ~20 orders of magnitude lower,
• and will evaporate on timescales that are ~30 orders of magnitude longer.

This means that it’s the lowest-mass black holes of all that are the locations where space is the most strongly-curved out of all the places in the Universe, and — in many ways — make for the most sensitive natural laboratory to test the limits of Einstein’s General Relativity.

When two neutron stars merge, they always produce a gravitational wave signal. However, dependent on a variety of factors, with mass being especially important, these neutron star mergers may or may not produce an electromagnetic signal as well. When they do, it does not arrive simultaneously with gravitational waves, but slightly later.

It might seem counterintuitive to think that the lowest-mass black holes in the Universe curve space more severely than the supermassive behemoths that populate the centers of galaxies, but it’s true. Curved space isn’t just about how much mass you have in one place, because what you can observe is limited by the presence of an event horizon. The smallest event horizons are found around the lowest-mass black holes. For metrics like tidal forces or black hole decay, being close to the central singularity is even more important than your overall mass.

This means that the best laboratories for testing many aspects of General Relativity — and to search for the first subtle effects of quantum gravity — will be around the smallest black holes of all. The lowest-mass ones we know come from neutron stars that merge to form black holes, just 2.5-to-3 times the Sun’s mass. The smallest black holes are where space is bent the most, and may yet hold the key to the next great breakthrough in our understanding of the Universe.