The better way to measure cosmic time

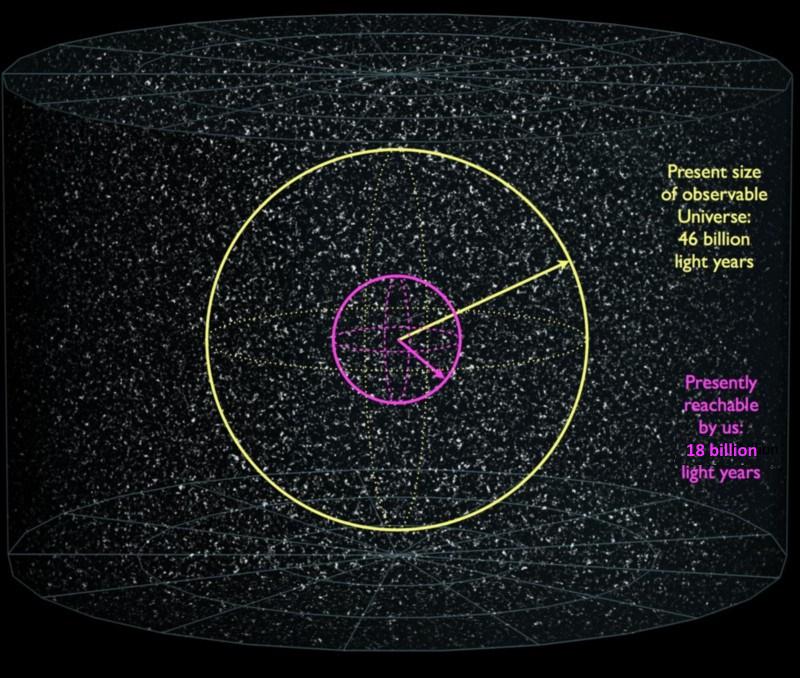
- Today, we can trace the Big Bang back to having occurred some 13.8 billion years ago, with the size of the observable Universe stretching to 46.1 billion light-years.
- But not only are units like “years” and “light-years” completely arbitrary and Earth-centric, they haven’t even had consistent definitions over the history of Earth.
- There might be better ways to measure time, especially for the Universe, but every alternative has its drawbacks, too.
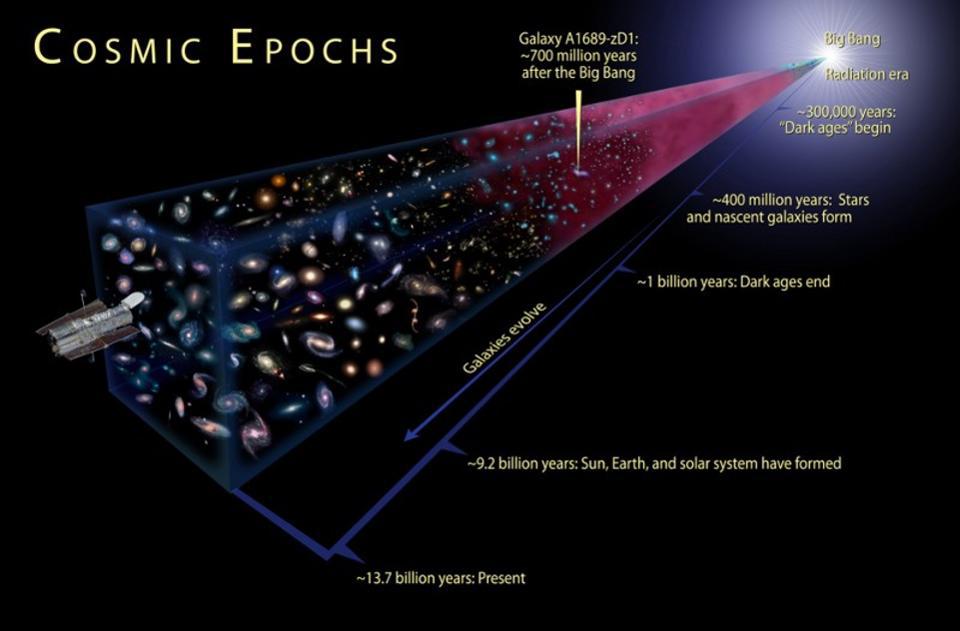
There are a number of grand questions we can ask about the Universe that cut right to the very core of what reality actually is, and were some of the biggest head-scratchers for all of human history. Questions like, “What is the Universe?” “How big is it?” and “Was it eternal, or did it spring into existence, and if so, when?” used to be some of the greatest philosophical mysteries, and yet the last 100 years have provided firm, scientific answers. We know what the Universe is, we know that the part observable to us is a hair over 92 billion light-years in diameter, and we know that the hot Big Bang, which started off the Universe as-we-know-it, occurred precisely 13.8 billion years ago, with an uncertainty in these values of just ~1% or so.
But why, of all the ways there are to measure time and distance, do we use such an Earth-centric set of units, like “years” and “light-years”? Isn’t there a better, more objective, more universal way to do it? Surely there is. At least, that’s what Jerry Bear thinks, writing in to ask:
“Why do cosmological calculations, such as the age or scale of the universe, utilize the provincial and wildly, woefully unequal to the task parameter of ‘year’? A year’s value as a measurement is so narrowly defined as to render it inappropriate to my mind. I mean, the basis of ‘year’ has only even existed for the most recent 30% of the universe’s age! And obviously the critical concept of a light-year is also tied to this parochial measurement.”
All of these are excellent points and are worth both expanding on and considering the alternatives to these somewhat arbitrary definitions. Let’s look at the science behind measuring cosmic time.
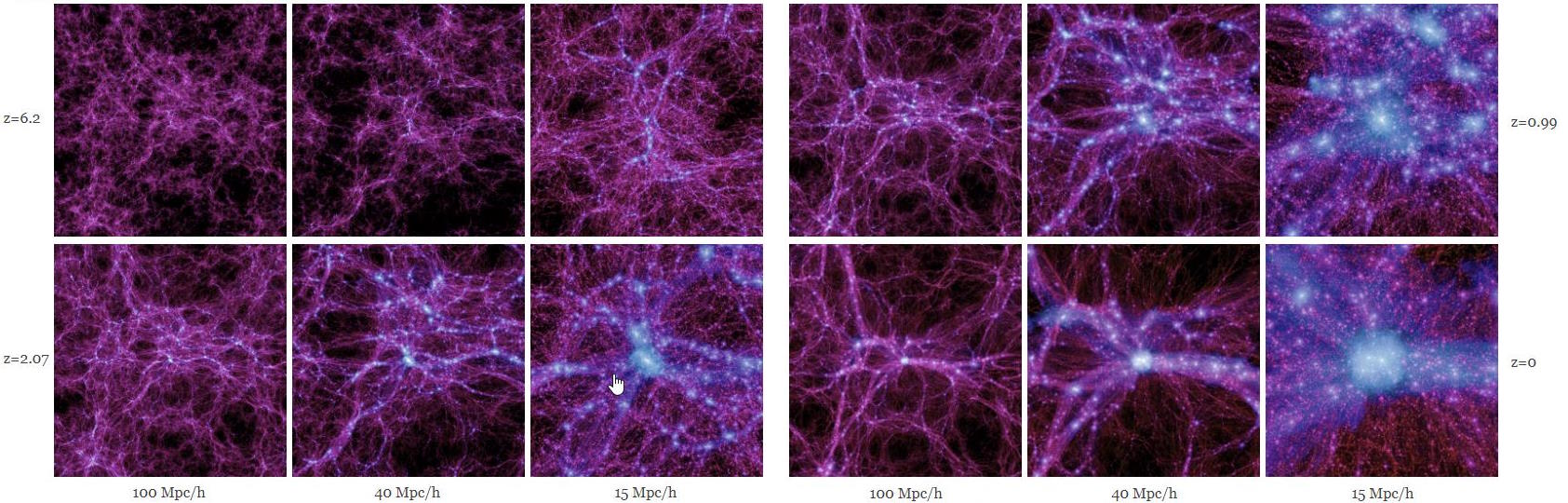
There are really only two ways, here on Earth, to make sense of the concept of the passage of time, and both make use of the regular recurrence of phenomena that are essential to not only human activity, but all biological activity. On shorter timescales, we have the concept of days, which are important for a number of reasons, including:
- they mark sunrise and sunset,
- they correspond to (roughly) a single complete rotation of Earth about its axis,
- they correspond to the period where most plants and animals experience both activity and dormancy,
all followed by a repeat of all of these phenomena, and more, on the next day. Meanwhile, on longer timescales, it’s very apparent that there are substantial differences between subsequent days, that themselves repeat if we wait long enough. Over the course of a year, days change in a variety of ways, including:
- sunrise and sunset times advance and retreat,
- the duration of daylight waxes and wanes,
- the Sun reaches a maximum in its height above the horizon, followed by a minimum, and a return to its original position again,
- the seasons change in a cycle,
- and the biological activity of plants, animals, and other living creatures change along with them.
Each year, with very little variation, the cycles of the previous year once again repeat themselves.

Based on this, it’s easy to understand why we came up with a system of timekeeping that is based around concepts such as a “day” and a “year,” as our activity on this planet is very tightly correlated with those periodic recurrences. But on closer inspection, for a variety of reasons, the notion of days and years as we experience them on Earth don’t particularly translate very well into a universal set of axioms for marking the passage of time.
For one, the duration of a day has changed substantially over the history of planet Earth. As the Moon, Earth, and Sun all interact, the phenomenon of tidal friction causes our day to lengthen and the Moon to spiral away from Earth. Some ~4 billion years ago, a “day” on planet Earth only lasted 6-to-8 hours, and there were over one thousand days in a year.
The variation in a year, however — or the time period required for Earth to complete a full revolution around the Sun — has only changed a little bit over the Solar System’s history. The largest factor is the changing mass of the Sun, which has lost about a Saturn’s worth of mass over its lifetime so far. This also pushes Earth out to distances a little bit farther from the Sun, and causes it to orbit slightly more slowly over time. This has caused the year to lengthen, but only slightly: by about 2 parts in 10,000. This corresponds to the year lengthening by about 2 hours from the start of the Solar System until today.

Even with all of the complex astrophysics taking place in our Solar System, then, it’s apparent that the duration of a year is probably the most stable large-scale feature that we could use to anchor our timekeeping to our planet. Since the speed of light is a known and measurable constant, a “light-year” then arises as a derived unit of distance, and also only changes by very little over time; it’s consistent over billions of years to the ~99.98% level.
The other major definition that we sometimes use is also, albeit indirectly, based on the definition of Earth orbiting the Sun to make up a year: the parsec. Instead of being based on time alone, it’s based on astronomical angles and trigonometry. As the Earth orbits around the Sun, the apparent positions of unmoving stars, relative to one another, will appear to change relative to one another, in the same way that if you open only one eye and then switch eyes, the closer objects will appear to shift relative to the more distant background objects.
In astronomy, we call this phenomenon “parallax,” and instead of the distance between two typical human eyes, we use the maximum distance between Earth’s position relative to the Sun: the diameter of its orbit, or about 300,000,000 kilometers. An object that appears to shift, relative to the distant background of objects, by one arc-second (1/3600th of a degree) is defined as one parsec: about 3.26 light-years.

But why would we tie our definition of time, which extends to the whole Universe, to the arbitrary motion of one planet in one galaxy around its parent star? It’s not objective, it’s not absolute, and it’s not useful beyond our own Earth-centric interests. Neither days nor years are universally applicable as measures of time, and neither light-years nor parsecs (or the associated quantities like kiloparsecs, megaparsecs, or gigaparsecs) are universally applicable as measures of distance.
There are, interestingly enough, ways to define time that are based on more objective, physical measures, and they don’t suffer from the same drawbacks that using an Earth-centric definition do. But there are some pretty good reasons for us not to use those measures of time, either, as each one comes with its own set of both pros and cons if you were to make an argument either for or against its use. Here are some options to consider, and you can decide for yourself whether you like it better or worse than the current year-based (and Earth-based) system of time that we’ve adopted for ourselves.

1.) The Planck time
Are you looking for a definition of time that doesn’t depend on anything except the fundamental constants of our Universe? You might want, then, to consider the Planck time! If we take three of the most fundamental, measurable constants of nature:
- the universal gravitational constant, G,
- the speed of light, c,
- and the quantum (i.e., the reduced Planck’s) constant, ħ,
then it’s possible to combine them in such a way to give a fundamental unit of time. Simply take the square root of (G multiplied by ħ divided by c5), and you’ll get a time that all observers can agree on: 5.4 × 10-43 seconds.
Although this corresponds to an interesting scale — the scale at which the laws of physics break down, because a quantum fluctuation on this scale wouldn’t make a particle/antiparticle pair, but rather a black hole — the problem is that there are no physical processes corresponding to this timescale. It’s simply mind-bogglingly small, and using it would mean we would need astronomically large numbers of the Planck time to describe even subatomic processes. The top quark, for example, the shortest-lived subatomic particle presently known, would have a decay time of about 1018 Planck times; a year would be more like 1051 Planck times. There’s nothing “wrong” with this choice, but it sure doesn’t lend itself to being intuitive.

2.) A measure of light, à la atomic clocks
Here’s a fun (and possibly uncomfortable) fact for you: all definitions of time, mass, and distance are completely arbitrary. There’s nothing significant about a second, a gram/kilogram, or a meter; we simply have chosen these values to be the standards we use in our daily lives. What we do have, however, are ways to relate any one of these chosen quantities to another: through the same three fundamental constants, G, c, and ħ, that we used to define the Planck time. If you make a definition for time or distance, for example, the speed of light will give you the other.
So why not just choose a particular atomic transition — where an electron drops from one energy level to another, and emits light of a very specific frequency and wavelength — to define time and distance? Frequency is just an inverse time, so you can derive a unit of “time” by measuring the time it takes one wavelength of that light to go past, and you can define “distance” by the length of one wavelength. This is how atomic clocks work, and this is the process we use to arrive at definitions for the second and the meter.
But, again, this is an arbitrary definition, and most transitions are too fast, with too small of a time interval, to be of practical, everyday use. For instance, the modern definition of the second is that it’s the time it takes for a photon emitted by the hyperfine structure of one Cesium-133 atom to undergo 9,192,631,770 (a little over 9 billion) wavelengths in a vacuum. So, don’t like years, or light-years? Just multiply anything you’d measure in those units by a little bit less than 3 × 1017, and you’ll get the new number in terms of this definition. Again, however, you wind up with astronomically large numbers for all but the fastest subatomic processes, which is a little cumbersome for most of us.

3.) The Hubble time
What if we went in the other direction, and instead of using smaller quantities that come from quantum properties, we went up to cosmic scales? The Universe, for example, expands at a specific rate: the expansion rate of the Universe, frequently known as either the Hubble parameter or the Hubble constant. Although we normally write it as a speed-per-unit-distance, like “71 km/s/Mpc” (or 71 kilometers-per-second, the speed, per megaparsec, the unit distance), it can also be written simply as an inverse time: 2.3 × 10-18 inverse seconds. If we flip that and convert that value to time, we get that one “Hubble time” equals 4.3 × 1017 seconds, or approximately the age of the Universe since the Big Bang.
If we use the speed of light to get a distance from this, we get that one “Hubble distance” is 1.3 × 1026 meters, or about 13.7 billion light-years, which is about 30% of the distance from here to the edge of the cosmic horizon.
Hey, this is looking pretty good! All of a sudden, we could work with distance scales and timescales comparable to truly cosmic ones!
Unfortunately, there’s a big problem with doing precisely this: the Hubble constant isn’t a constant with time, but drops continuously and in a complex fashion (depending on the relative energy densities of all the different components of the Universe) as the Universe ages. It’s an interesting idea, but we’d have to redefine distances and times for every observer in the Universe, dependent upon how much time has passed for them since the start of the hot Big Bang.

4.) The spin-flip transition of hydrogen atoms
You might find yourself frustrated at how each of our attempts thus far to come up with a better definition of time has only led to a worse outcome for cosmic scales. But there’s one possibility worth considering: the most common quantum transition in the whole Universe. You see, whenever you form neutral hydrogen, it forms as an electron binds to the atomic nucleus, which is almost always just a single, bare proton. When the electron reaches the ground state, there are two possibilities for how it will be configured relative to the proton.
- Either the electron and proton will have opposite (anti-aligned) quantum spins, where one has spin +½ and one has spin -½,
- or the electron and proton will have identical (aligned) quantum spins, where either both are +½ or both are -½.
If the spins are anti-aligned, then that’s truly the lowest energy state. But if they’re aligned, there’s a certain probability that the spin of the electron can spontaneously flip, emitting a very specific photon of a very particular frequency: 1,420,405,751.77 Hz. But that’s not the interesting part, as manipulating that frequency yields a time of about 0.7 nanoseconds and a length of about 21 centimeters.
The interesting part is that the transition rate is astronomically slow: 2.9 × 10-15 inverse seconds. If we translate that into a cosmic time and a cosmic length scale, we get about 10.9 million years and 10.9 million light-years, equivalent to about 3.3 megaparsecs. Of all the fundamental constants of nature that I, personally, know of, this is the most commonly encountered one that could give us cosmically superior timescales and distance scales to years and light-years (or parsecs) in all the Universe.
The most important aspect, however, is this: the specific definition of time that we choose is arbitrary, and unimportant to the physical answer we get concerning questions of duration or distance. As long as we’re consistent that how we define a time interval doesn’t change over the history of the Universe, all of these answers will be equivalent to one another.
What’s the major difference, then, that arises between our different definitions of time?
It is, in the end, our own very human ability to wrap our minds around it, and make sense of these numbers for ourselves.
In the astronomical literature, you’re likely to encounter times measured in some number of years, and distances measured in either Astronomical Units (A.U.). parsecs (pc), kiloparsecs (kpc), megaparsecs (Mpc), or gigaparsecs (Gpc), depending on whether we’re talking about Solar System, stellar, galactic, intergalactic, or cosmic distance scales. But because as humans, we understand the concept of a year fairly intuitively well, we simply multiply by the speed of light to get a distance, light-years, and go from there. It’s not the only option, but it’s the most popular one so far. Perhaps, in the far future, humanity will no longer be tethered to Earth, and when we move beyond our home world, we may at last move beyond these Earth-centric units as well.
Ethan is on medical leave until May 6th. Please enjoy a republication of this article from the Starts With A Bang archives!