Attosecond spectroscopy wins 2023’s Nobel Prize in Physics

If you want to understand and measure the world around you, one of the most important tools at your disposal is the ability to image — or take a snapshot — of precisely what’s occurring. In the 19th century, photography meant holding your subject perfectly still while you accumulated large amounts of light: several seconds worth of it. In more modern times, we can perform high-speed photography, using a shorter “pulse” of light to image an individual, brief moment in the life of objects as they naturally occur, including objects in motion. We can do this with visible light for macroscopic objects, but we can do it with a variety of wavelengths on microscopic scales with a special type of technology: high-speed laser pulses.

Because individual atoms and molecules are so small, as little as an Angstrom (or ~10^-10 meters) across, that means that changes/transitions occurring within them — driven by electrons — can occur in as little as that distance, 10^-10 meters, divided by the speed of light, or 3 × 10⁸ m/s. That works out to a few attoseconds, where a single attosecond is just 10^-18 seconds. Can we perform imaging that quickly? We can if we can generate short-enough laser pulses, and that’s exactly what the 2023 Nobel Prize in Physics is for, awarded to Pierre Agostini, Ferenc Krausz, and Anne L’Huillier. Here’s the science behind this incredible advance.

By firing a pulse of light at a semi-transparent/semi-reflective thin medium, researchers can measure the time it must take for these photons to tunnel through the barrier to the other side. Although the step of tunneling itself may be instantaneous, the traveling particles are still limited by the speed of light. By taking high-speed images of this light pulse, we can construct a movie that appears continuous.

When you watch the world unfold with your own eyes, your brain interprets the images you see as though reality were being written in a continuous, unbroken stream: like everything smoothly moves from one moment to the next. Down at the quantum level, however, we know this isn’t true. What’s actually happening, inside your anatomy, is that:

• individual quanta of light are arriving at the rods and cones in your retina,
• stimulating the photoreceptor molecules that live inside,
• which excite the electrons to a higher energy level,
• and then those electrons de-excite,
• producing an electrical impulse in the cells inside your body,
• that trigger a neural response that sends a signal to your brain,
• which then generates an image in your brain’s visual cortex,
• which your brain interprets relative to the last “image” it generated,
• while the newly arriving quanta of light on your retina start the cycle all over again.

The human brain and body, remarkably, can perform this task dozens or even hundreds of times per second, allowing you to interpret the macroscopic world as constantly moving and shifting.

This synthesis of three different sets of spectral lines from a mercury vapor lamp shows the impact that a magnetic field can have. In (A), there is no magnetic field. In (B) and (C), there is a magnetic field, but they’re oriented differently, explaining the differential splitting of the spectral lines. Many atoms exhibit this fine-structure or even hyperfine-structure without the application of an external field, and those transitions are essential when it comes to constructing a functional atomic clock. Many transitions, such as the ones shown here, are discrete, rather than continuous processes.

But in reality, many of the things happening in the world aren’t continuous processes, but rather occur all at once in a single “jump” from one state to the next: in a series of discrete, rather than continuous, processes. The deeper down into the microscopic world we look — at processes that occur on shorter and shorter distance scales — the faster we need to probe, or photograph, nature in order to detect these discrete transitions. Some examples of the relationship of how distance scales to the speed of a pulse include:

• microsecond (~10^-6 s) pulses, which allow you to image changes on the scale of a few hundred meters,
• nanosecond (~10^-9 s) pulses, which allow you to image changes on the scale of a few tenths of a meter,
• picosecond (~10^-12 s) pulses, which allow you to image changes on the scale of a few hundred microns (the scale of a paramecium),
• femtosecond (~10^-15 s) pulses, which allow you to image changes on the scale of a few hundred nanometers (the scale of large molecules),
• and attosecond (~10^-18 s) pulses, which take you down to Angstrom-level scales, enabling you to view changes on the scale of a single atom.

These correspondences are for instantaneous transitions: transitions that occur at the speed of light, or the limiting speed of the Universe. If you can “pulse” your light fast enough, you can theoretically detect changes governed by the transition of even a single quantum particle.

By “pumping” electrons into an excited state and stimulating them with a photon of the desired wavelength, you can cause the emission of another photon of exactly the same energy and wavelength. This action is how the light for a laser is first created. That light, depending on a variety of properties, can then be leveraged for many different purposes.

The shortest possible “pulse” that you can generate will encode only one wavelength for your light wave: the length of a single period of that light. Light that’s visible to human eyes, for example, falls in the wavelength range of 400 nanometers (violet light) to 700 nanometers (red light), where a single wavelength of that light takes between 1.3 and 2.3 femtoseconds to go from crest-to-trough-to-crest again. That’s fast, but it’s not fast enough to take the types of images physicists really want to take: the types of images that get you all the way down to probing atomic scales.

But there’s a technique that does allow you to take light of a relatively normal wavelength and create pulses that are both regularly-spaced out in time and that also occur with a consistent pulse shape and duration that can be either longer or shorter in time than the original wavelength’s duration: leveraging the quantum property of superposition. If you take multiple different waves, with different wavelengths, you can superimpose them atop one another to create pulses of either long or short duration that are “peaked” at a specific, controllable frequency. This type of pulsing enables a great many types of science, from “beat frequencies” with sound waves to the ultrafast lasers that are used to probe the fundamental quantum properties of matter.

When two waves that are close together in frequency are superimposed atop one another, they interfere both constructively and destructively, enabling the creation of “beats” of a different frequency than either of the individual waves on their own. This same principle, of superposition, applies to light just as well as it does to sound.

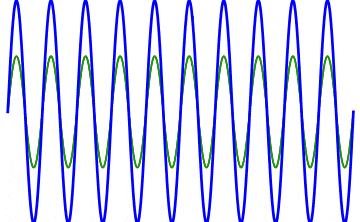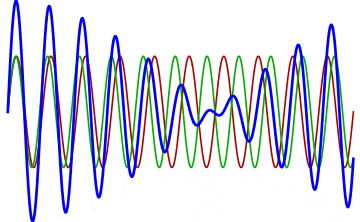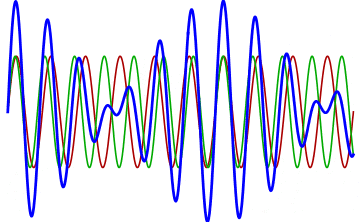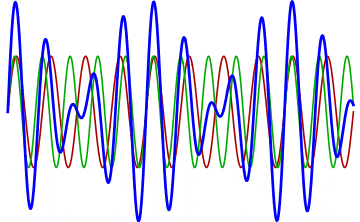
The key to reaching the attosecond level, as far as the speed of your pulses go, is to combine large numbers of short-wavelength species of light, or many “modes” of waves, together. Back in the 1980s, many thought that “femtoseconds” would be about as fast as light could get, as that was the shortest pulse you could make with a standard laser that only produced a single frequency of light. But others were actively researching this alternative possibility, first from the perspective of generating additional (higher) frequencies of light that could be controlled, and then from the perspective of combining those newly-generated light waves together to produce these faster-than-ever pulses.

Although the Nobel Committee announced that the 2023 prize in physics goes to Pierre Agostini, Ferenc Krausz, and Anne L’Huillier, the truth is that Anne L’Huillier — who it should be mentioned is only the fifth woman to win the Physics Nobel (but the third in the past five years) after Marie Curie, Maria Goeppert-Mayer, Donna Strickland and Andrea Ghez — is the name that needs to come first in the story of attosecond spectroscopy, as it was her work that laid the foundation for attosecond-speed pulses to even get created. The best and easiest analogy for how she did it is to think about “overtones” on a guitar string.

While a string on a guitar has a fundamental frequency that it vibrates at, producing the “tone” illustration at right, you can also “pin down” nodes on the string to cause it to vibrate at higher frequencies: the overtones. The first three overtones illustrate pinning nodes down at one-half, one-third, and one-quarter of the original string length, respectively.

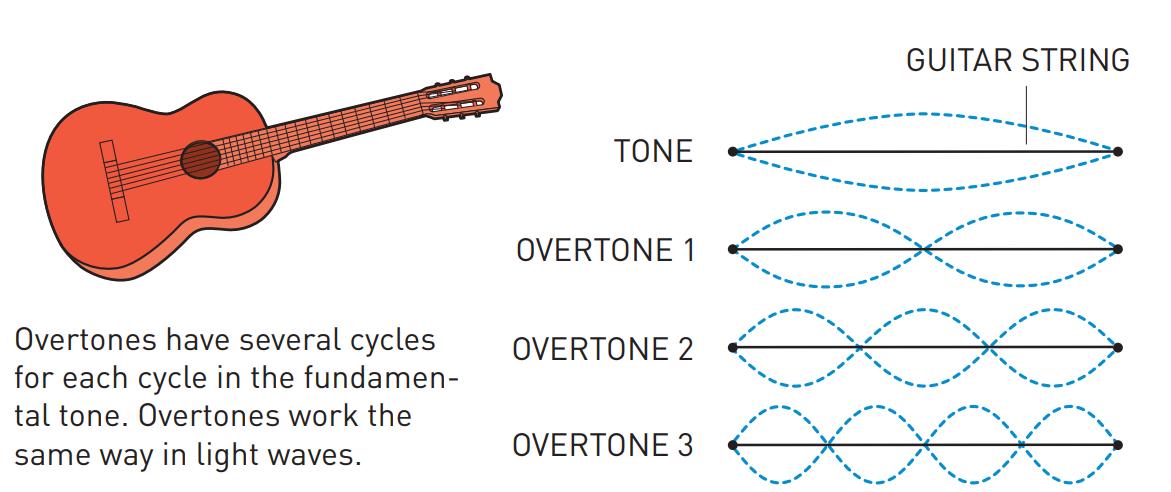
If you want to play a note on the guitar, all you have to do is either strike or pluck the string, and it will vibrate back-and-forth between the two “nodes” of the string, or the “ends” of where it’s pinned to the fretboard. That produces waves of a particular wavelength (you can see “half” of a full wavelength in the illustration marked “tone”) that, depending on the string thickness and tension, produces sound of a specific frequency that you can hear.

However, if you use your finger to create another “node” elsewhere on the string, in addition to the first two that correspond to the “ends” of the string, you can create what are known as “overtones,” where the string can only vibrate at certain wavelengths that are a fraction of the wavelength of the main tone. For example, if you pluck an open guitar string and you put your finger, loosely, on:

• no fret, you get the basic tone, and a wave whose wavelength is twice the length of the string.
• the 12th fret, you get the 1st overtone, and a wave whose wavelength is equal to the length of the string.
• the 7th fret, you get the 2nd overtone, and a wave whose wavelength is ⅔ the length of the string.
• the 5th fret, you get the 3rd overtone, and a wave whose wavelength is ½ the length of the string.

That’s how tones and overtones work for sound waves. But you can actually create overtones using lasers for light waves, and Anne L’Huillier was the person who figured out precisely how to make that happen.

The Royal Swedish Academy of Sciences awarded the Nobel Prize in Physics 2023 to Pierre Agostini, Ferenc Krausz and Anne L’Huillier, illustrated here from left-to-right, “for experimental methods that generate attosecond pulses of light for the study of electron dynamics in matter.”

The first big step she and her team took was to use an infrared laser and to transmit the light it emitted through a noble, inert gas. It didn’t just produce overtones in the light, but — very interestingly — extremely strong overtones that went way up the scale in number: not just to 2 or 3 but into the double digits. While previous, similar experiments had demonstrated the existence of overtones by passing laser light through a noble gas before, using the infrared laser led to stronger overtone signals (i.e., with greater wave amplitude) and also to higher overtone frequencies (i.e., at shorter wavelengths) than prior experiments that had been performed with shorter wavelengths of laser light.

This is counterintuitive! Most of us would have expected that, if you wanted to produce short wavelengths of light, you would start with a short-wavelength laser signal and try to coax the overtones out of that. But for some reason — reasons that L’Huillier continued to explore with subsequent research throughout the late 1980s and all of the 1990s — that longer wavelength infrared light actually led to the production of stronger, shorter-wavelength overtones through this mechanism. It would be as if the thickest guitar string, the one that produces the lowest notes, actually gave you the highest-pitched sounding overtones!

When low-frequency, long-wavelength laser light interacts with an atom, the electric and magnetic fields can unbind an electron from the atom temporarily. When the electron recombines with the atom, it must shed excess energy, which causes it to emit higher-frequency, shorter-wavelength light that’s an overtone of the original laser light’s frequency/wavelength. This diagram shows the electron’s behavior.

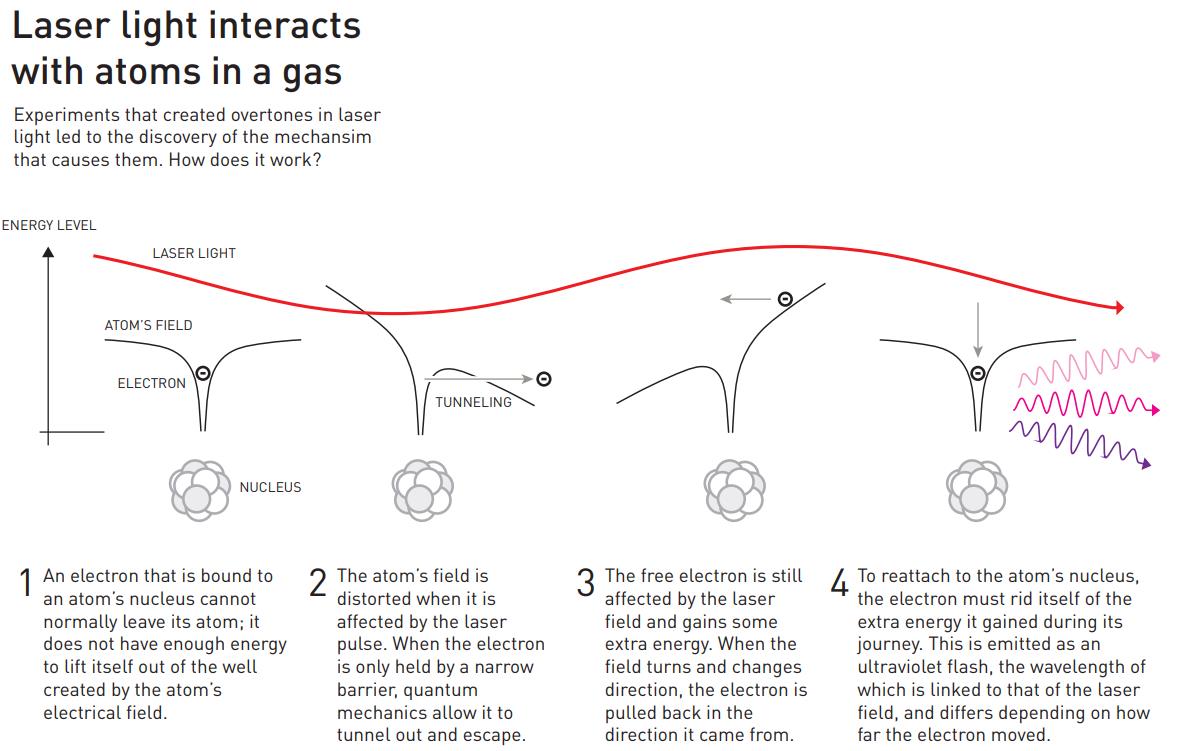
The physics of how this occurs is diagrammed out, above. Light, as we must remember, is an electromagnetic wave, with in-phase, oscillating electric and magnetic fields acting perpendicular to the direction of the wave’s propagation. When the light passes through a gas made out of atoms, the electrons around those atoms respond to the electromagnetic fields that the passing light wave generates, and in the proper circumstances, some of those electrons can even escape the atoms that they’re bound to, creating a briefly ionized atom and a free electron.

However, the electric field from the light wave is oscillating, and when it reverses direction, it can cause that free electron to rush back to the atomic nucleus it just became unbound from, causing it to release that energy as a pulse (or a series of pulses) of light. Just as electrons cascading down the energy levels of a hydrogen atom can produce both high-energy and low-energy light, the electrons that transition from “free” back to “bound” can produce light that’s only a fraction of the wavelength of the laser light that was passed through the noble gas. As the electron sinks down to the lowest energy level, it normally produces an ultraviolet photon: a photon much shorter in wavelength than the infrared light that originally stimulated the atom.

When laser light is shone through a gas, the behavior of the electrons causes the emission of many “overtones” of light. When that light is then recombined with the original, delayed light from the stimulating laser, extremely rapid experiments can then be performed with that combined beam.

That’s where the work of the two other Nobel Laureates in Physics for 2023 comes in: the work of Pierre Agostini and Ferenc Krausz. By using the ultraviolet photons that are produced by this technique, and by tuning the laser frequency so that specific overtones of the light’s original frequency are stimulated by the electron transitions, the way those overtones sum up together from being superimposed atop one another can create pulses of ultraviolet light that are only hundreds of attoseconds long. Agostini and Krausz — or more accurately their respective groups in France and Austria — first identified and tested these pulses back in 2001.

Agostini’s group combined this superposition of overtones, what’s called a “pulse train” by some, with light from the original laser pulse, enabling them to measure how the overtones were in phase with one another. They set a record for shortest pulse ever at that time: each pulse was just 250 attoseconds long.

Contemporaneously, Krausz’s group invented a technique that enabled them to isolate one single pulse from the “pulse train” and measure its duration. It was longer than Agostini’s group at 650 attoseconds, but it still broke the femtosecond barrier and, more importantly, allowed Krausz’s group to track and study the process by which electrons were pulled away from and then shunted back onto their atoms.

By applying the technique of attosecond spectroscopy, it was found that photoemission from liquid water electrons shows a time delay of 50-70 attoseconds compared with photoemission from the gaseous (water vapor) phase. This research was enabled by the pioneering work of Pierre Agostini, Ferenc Krausz and Anne L’Huillier: 2023’s Nobel Laureates in physics.

The foundational research of these three individuals and their research groups — Anne L’Huillier, Pierre Agostini, and Ferenc Krausz — not only demonstrated that attosecond pulses could be observed and measured, but also controlled, which makes them useful for performing experiments. By creating these short bursts of light and firing them at atoms and molecules, the movement of individual electrons can be studied to greater precision than ever before. Currently, pulses can be created that are less than 100 attoseconds long, and many foresee that the goal of getting down to single-digit attosecond pulse lengths will be within reach in the coming decades.

It’s incredible that the physical processes that power so much of modern life, from electronics to materials science to medical diagnostics and more, come down to what electrons within a single atom or molecule are doing, and how they transition from one state to another.

One of my favorite parts of the Nobel Prize in Physics is that it showcases what a diverse and varied field physics truly is. Although I was anticipating that the prize would either go for quantum computation, exoplanets in astronomy, advances in photonics, or to some aspect of condensed matter physics, the reality is that advances are continuously occurring all over a wide variety of sub-fields, not just the splashiest and most well-known ones. Let’s appreciate these advances in ultra-fast physics and attosecond spectroscopy for what they are and what they enable us to do, and here’s to the pioneering work of 2023’s Nobel Laureates in Physics: Anne L’Huillier, Pierre Agostini, and Ferenc Krausz!