Ask Ethan: What’s It Like When You Fall Into A Black Hole?

It’s the ultimate way to go… and yet, it still isn’t what you’d expect.

There are many terrifying ways that the Universe can destroy something. In space, if you tried to hold your breath, your lungs would explode; if you exhaled every molecule of air instead, you’d black out within seconds. In some locations, you’d freeze solid as the heat was sucked out of your body; in others it’s so hot that your atoms would turn into a plasma. But of all the ways the Universe has to dispose of someone, I can think of none more fascinating than to send someone inside a black hole. So does Event Horizon Telescope scientist Heino Falcke, who asks:

[W]hat is it like to be/fall inside a rotating black hole? This is not observable, but calculable… I have talked with various people who have done these calculations, but I am getting old and keep forgetting things.

It’s a tremendously interesting question, and one that science can answer. Let’s find out.

According to our theory of gravity, Einstein’s General Relativity, there are only three things that determine the properties of a black hole. They are the following:

1. Mass, or the total amount of matter and the equivalent amount of energy (via E = mc²) that went into both forming and growing the black hole to its present state.
2. Charge, or the net electric charge that exists in the black hole from all the positively and negatively charged objects that fell into the black hole over its history.
3. Angular momentum, or spin, which is a measure of the total amount of rotational motion that the black hole inherently has.

Realistically, all the black holes that physically exist in our Universe should have large masses, significant amounts of angular momentum, and negligible charges. This complicates matters tremendously.

When we typically think of a black hole, we imagine the much simpler kind: one described by its mass only. It has an event horizon that surrounds a single point, and a region surrounding that point from which light cannot escape. That region is perfectly spherical, and has a boundary separating the regions where light can escape from the region where it cannot: the event horizon. The event horizon is located a specific distance (the Schwarzschild radius) away from the singularity in all directions equally.

This is an simplified version of a realistic black hole, but a good place to start thinking about the physics that occurs in two distinct places: outside the event horizon and inside the event horizon.

Outside of the event horizon, gravity behaves just like you’d conventionally expect. Space is curved by the presence of this mass, which causes every object within the Universe to experience an acceleration towards the central singularity. If you were to start off a large distance away from this black hole, at rest, and allowed an object to fall into it, what would you see?

Assuming you were able to remain stationary, you’d see this infalling object slowly accelerate away from you, towards this black hole. It would speed up towards the event horizon, remaining the same color, and then something strange would happen. It would appear to slow down, fade away, and get redder in color. It wouldn’t completely disappear though; not quickly, and not ever. Instead, it would just approach that state: getting fainter, redder, and harder to detect. The event horizon is like an asymptote for the object’s light; you’ll always be able to see it if you look hard enough.

Now, imagine the same scenario, but this time, don’t imagine you’re observing the infalling object from afar. Instead, imagine that you yourself are the infalling object. The experience you’d have would be extremely different.

The event horizon appears to get much larger far faster than you’d expect, as the curvature of space gets severe. Around the event horizon, space is so distorted that you begin to see multiple images of the outside Universe, as though they were reflected and inverted.

And once you crossed inside the event horizon, you’d not only still see the outside Universe, but a portion of the Universe inside the event horizon. The light you received would blueshift, but then redshift again, as you inevitably fell towards the singularity. In the last moments, space would bizarrely look completely flat.

The physics of this is complicated, but the calculations are straightforward, and were most elegantly performed by Andrew Hamilton of the University of Colorado in a series of papers spanningthe late 2000s to the early 2010s. Hamilton has also created a series of spectacular visualizations on what you would see as you fell into a black hole, based on these calculations.

There are a number of lessons we can learn from examining these results, and many of them are counterintuitive. The way to try and make sense of it is to change the way you visualize space. Normally, we think of space as a stationary fabric and we think of an observer as being “plunked” down somewhere. But inside an event horizon, you’re always in motion. Space is fundamentally in motion — like a moving walkway — continuously, moving everything in it towards the singularity.

It moves everything so quickly that even if you accelerate directly away from the singularity with an infinite amount of force, you’ll still fall towards the center. Objects from outside the event horizon will still have their light encounter you from all directions, but you’ll only ever be able to see a portion of the objects from inside the event horizon.

The line that defines the boundary between what any observer can see is mathematically described by a cardioid, where the largest-radius component of the cardioid touches the event horizon and the smallest-radius component terminates at the singularity. This means that the singularity, even though it’s a point, does not inevitably connect everything that falls in to everything else. If you and I fall into opposite sides of the event horizon at the same time, we’ll never be able to see each other’s light after the horizon-crossing takes place.

The reason for this is the always-in-motion fabric of the Universe itself. Inside the event horizon, space moves faster than light, and that’s why nothing can ever escape from the black hole. It’s also why, once inside the black hole, you start seeing bizarre things like multiple images of the same object.

You can understand this by asking a question like, “where is the singularity?”

From inside a black hole’s event horizon, if you move in any direction, you’ll eventually encounter the singularity itself. Therefore, surprisingly, the singularity appears in all directions! If your feet are directly pointed in the direction you’re accelerating, you’ll see them below you, but you’ll also see them above you. All of this is straightfoward to calculate, even though it’s tremendously counterintuitive. And that’s just for the simplified case: the non-rotating black hole.

Now, let’s come to the physically interesting case: where the black hole spins. Black holes owe their origin to systems of matter, like stars, which always spin at some level. In our Universe (and in General Relativity), angular momentum is an absolutely conserved quantity for any close system; there’s no way to get rid of it. When a collection of matter collapses down to a radius smaller than the radius of an event horizon, the angular momentum gets trapped inside there, just like the mass does.

The solution we get is now much more complicated. Einstein put forth General Relativity in 1915, and Karl Schwarzschild derived the non-rotating black hole solution a couple of months later, in early 1916. But the next step in modeling this problem in a more realistic fashion — to consider what if the black hole also has angular momentum, instead of mass alone — wasn’t solved until Roy Kerr found the exact solution in 1963.

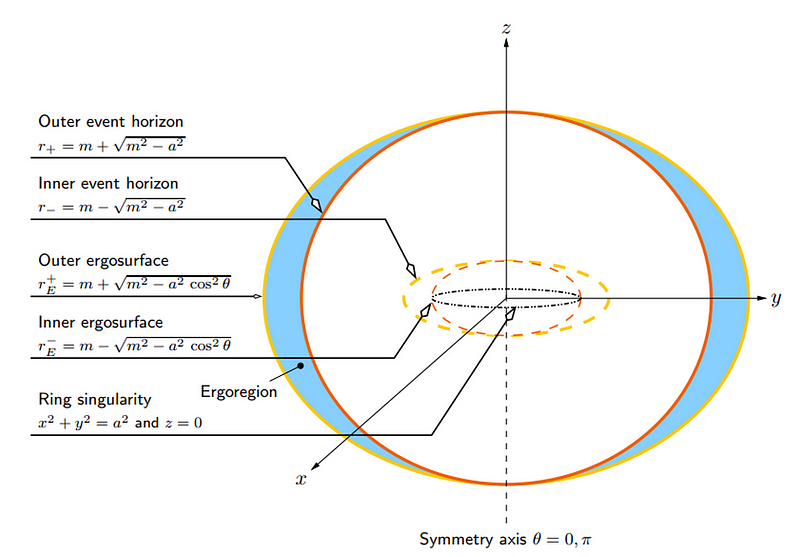
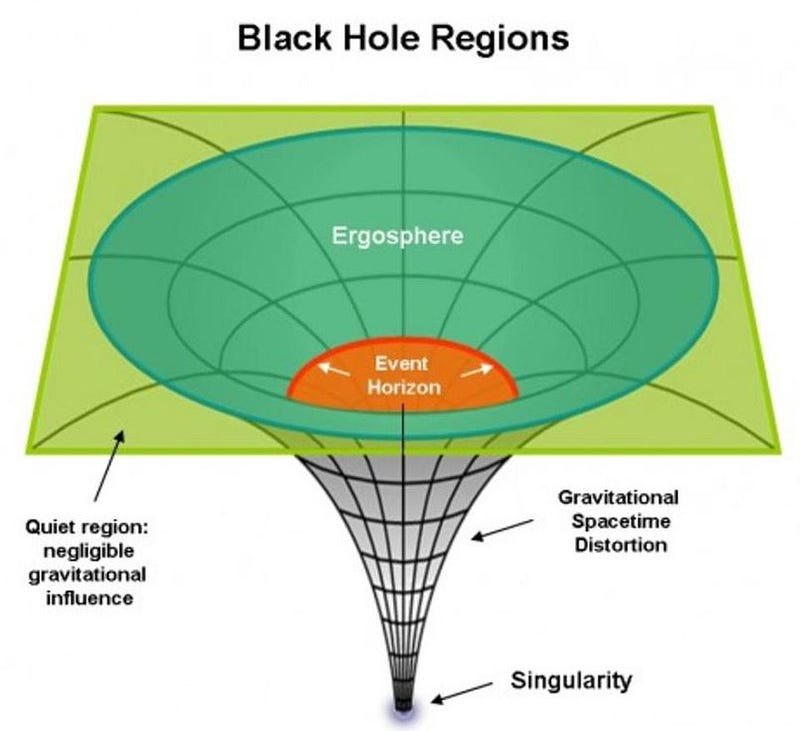
There are some fundamental and important differences between the more naive, simpler Schwarzschild solution and the more realistic, complex Kerr solution. In no particular order, here are some fascinating contrasts:

1. Instead of a single solution for where the event horizon is, a rotating black hole has two mathematical solutions: an inner and and outer event horizon.
2. Outside of even the outer event horizon, there is a place known as the ergosphere, where space itself is dragged around at a rotational speed equal to the speed of light, and particles falling in there experience enormous accelerations.
3. There is a maximum ratio of angular momentum to mass that is allowed; if there is too much angular momentum, the black hole will radiate that energy away (via gravitational radiation) until it’s below that limit.
4. And, perhaps most fascinatingly, the singularity at the black hole’s center is no longer a point, but rather a 1-dimensional ring, where the radius of the ring is determined by the mass and angular momentum of the black hole.

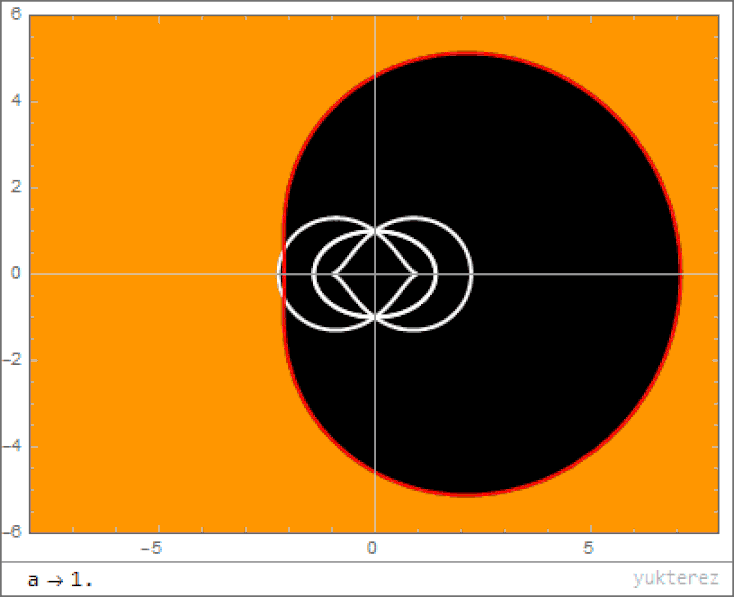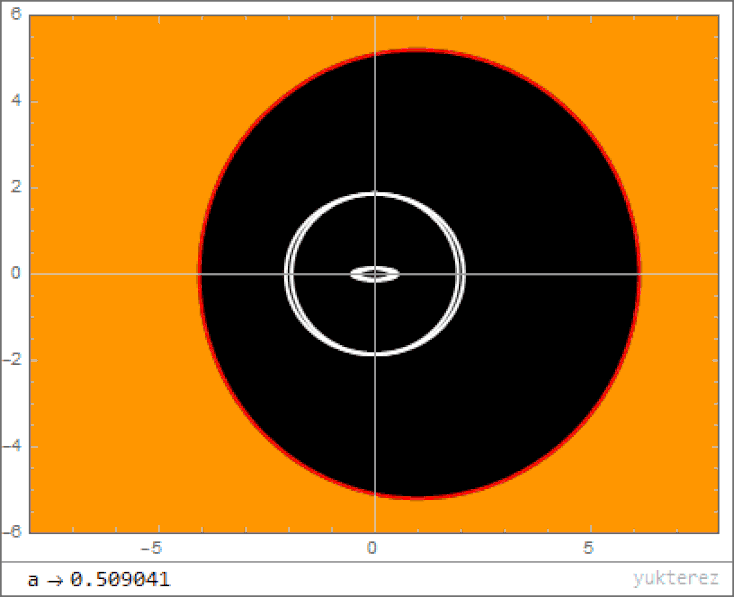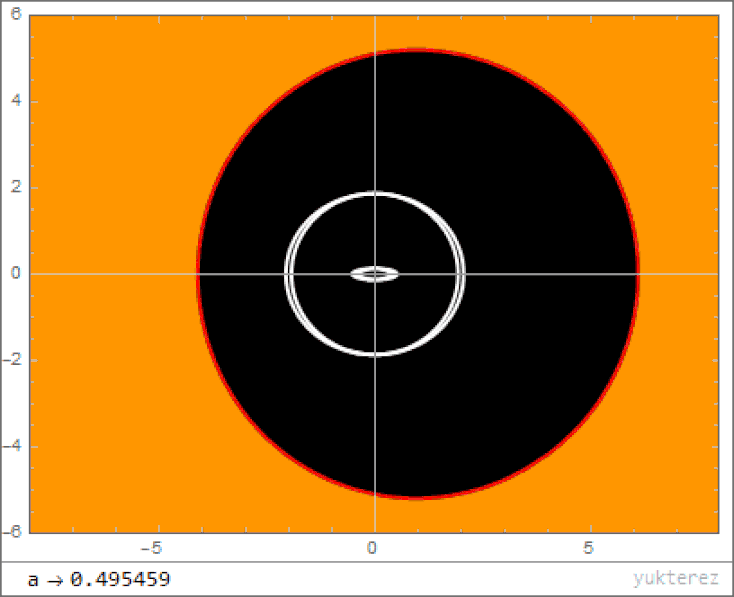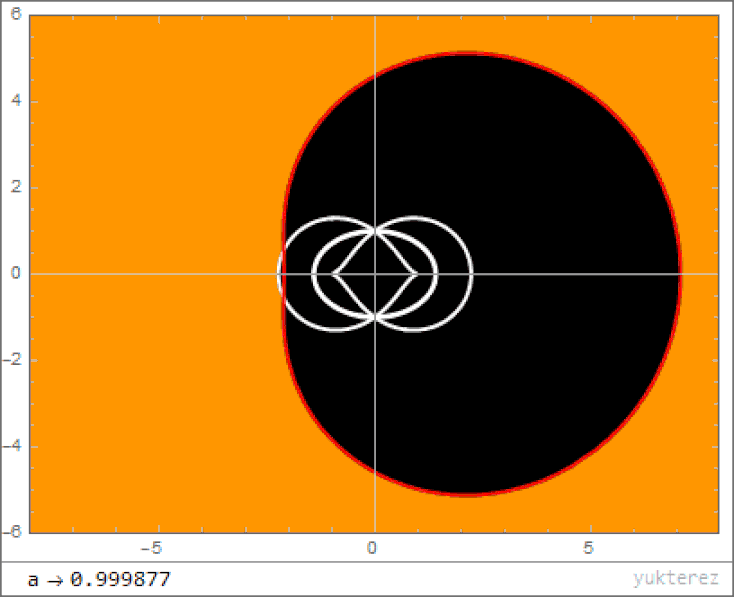
With all this in mind, what happens when you fall inside a rotating black hole? The same thing that happens when you fall into a non-rotating black hole, except that all of space doesn’t behave as though it’s falling towards a central singularity. Instead, space also behaves as though it’s getting dragged around along the direction of rotation, like a spinning vortex. The larger the ratio of angular momentum to mass, the faster it rotates.

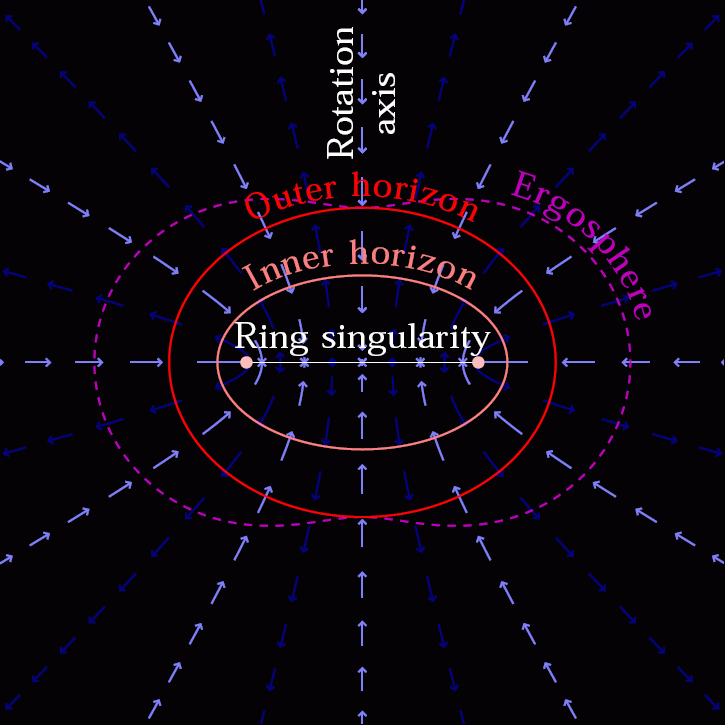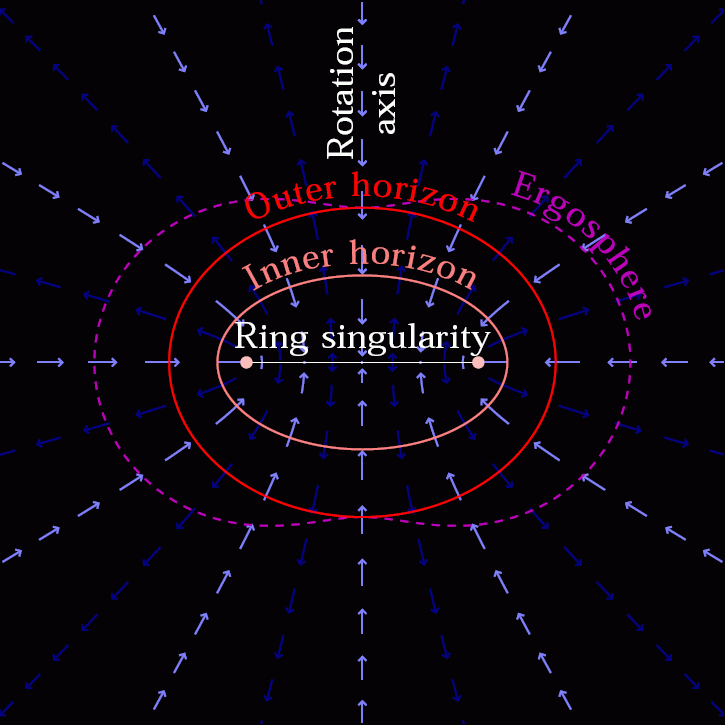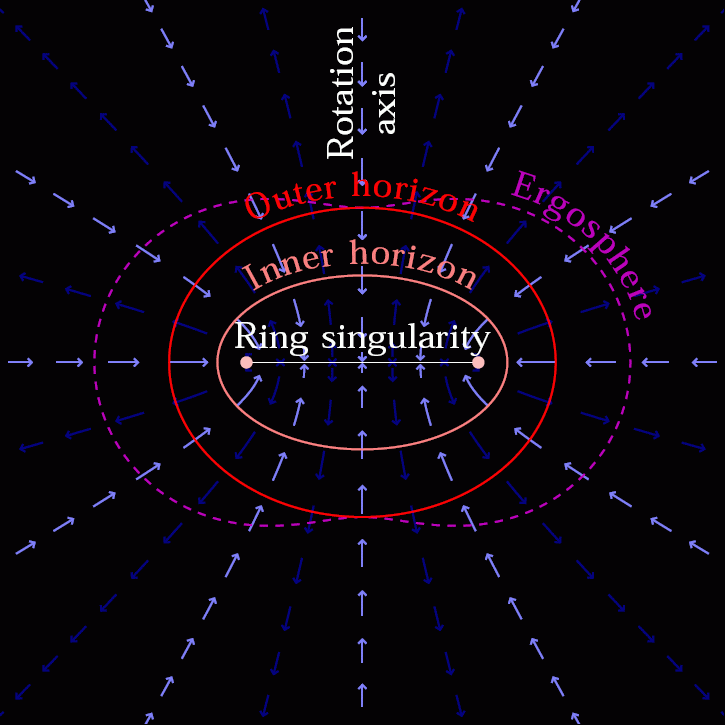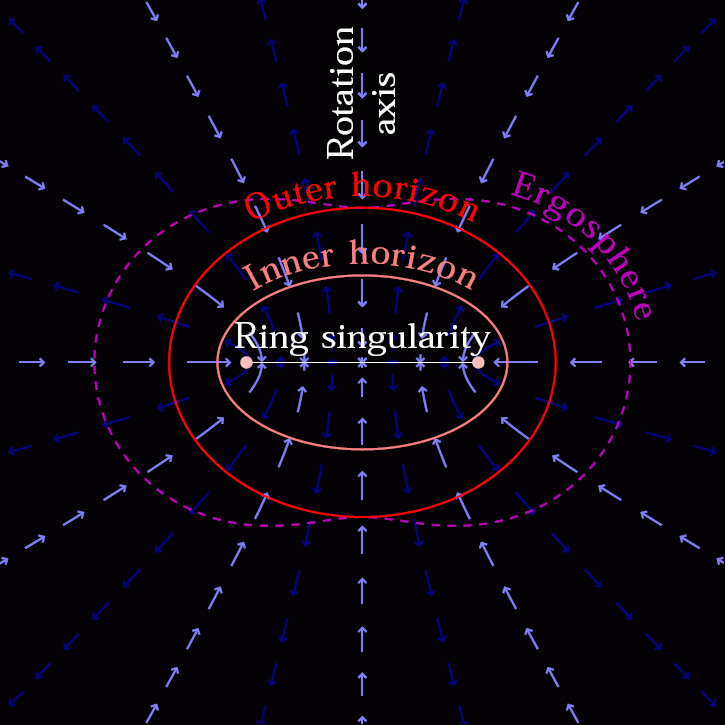
This means that if you see something fall in, you’ll see it get fainter and redder, but also smeared out into a ring or a disk along the direction of rotation. If you fall in, you’ll get whipped around like you’re on some maddening carousel that sucks you towards the center. And when you reach the singularity, it will be a ring; different parts of your body will encounter the singularity — at the inner ergosurface of the Kerr black hole — at different spatial coordinates. As you approach the singularity from inside the event horizon, you’ll gradually become unable to see the other parts of your own body.

The most profound piece of information you should take away from all of this is that the fabric of space itself is in motion, and the event horizon is defined as the location where even if you’re able to move at the ultimate cosmic speed limit — the speed of light — in whatever direction you choose, you will always wind up encountering the singularity.

The visualizations by Andrew Hamilton are the best, most scientifically accurate simulations of what falling into a black hole truly looks like, and are so counterintuitive that all I can truly recommend is that you watch them over and over again until you fool yourself into thinking you understand it. It’s eerie, beautiful, and if you’re adventurous enough to ever fly yourself to a black hole and cross inside the event horizon, it’ll be the last thing you ever see!

Send in your Ask Ethan questions to startswithabang at gmail dot com!