Ask Ethan: What Is An Electron?

Sometimes, the simplest questions of all are the most difficult to meaningfully answer.
If you were to take any tiny piece of matter in our known Universe and break it up into smaller and smaller constituents, you’d eventually reach a stage where what you were left with was indivisible. Everything on Earth is composed of atoms, which can further be divided into protons, neutrons, and electrons. While protons and neutrons can still be divided farther, electrons cannot. They were the first fundamental particles discovered, and over 100 years later, we still know of no way to split electrons apart. But what, exactly, are they? That’s what Patreon supporter John Duffield wants to know, asking:
Please will you describe the electron… explaining what it is, and why it moves the way it does when it interacts with a positron. If you’d also like to explain why it moves the way that it does in an electric field, a magnetic field, and a gravitational field, that would be nice. An explanation of charge would be nice too, and an explanation of why the electron has mass.
Here’s what we know, at the deepest level, about one of the most common fundamental particles around.

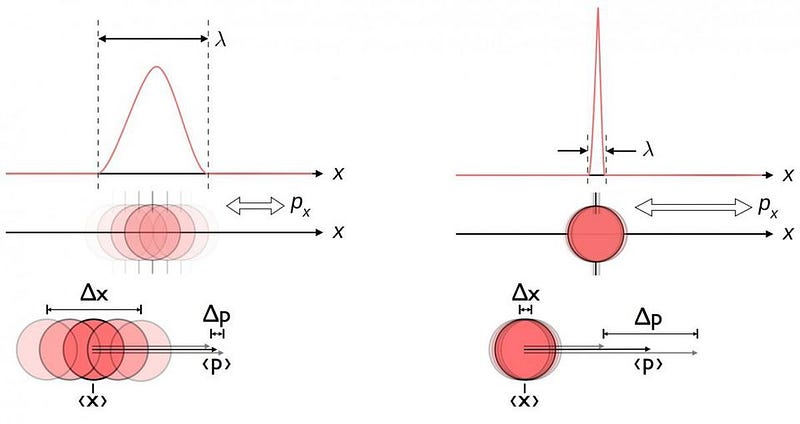
In order to understand the electron, you have to first understand what it means to be a particle. In the quantum Universe, everything is both a particle and a wave simultaneously, where many of its exact properties cannot be perfectly known. The more you try and pin down a particle’s position, you destroy information about its momentum, and vice versa. If the particle is unstable, the duration of its lifetime will affect how well you’re able to know its mass or intrinsic energy. And if the particle has an intrinsic spin to it, measuring its spin in one direction destroys all the information you could know about how it’s spinning in the other directions.
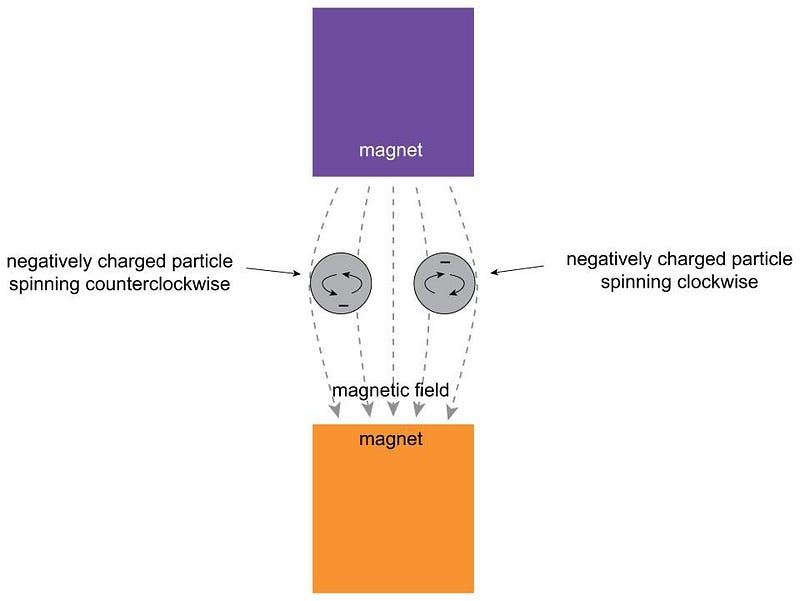
If you measure it at one particular moment in time, information about its future properties cannot be known to arbitrary accuracy, even if the laws governing it are completely understood. In the quantum Universe, many physical properties have a fundamental, inherent uncertainty to them.
But that’s not true of everything. The quantum rules that govern the Universe are more complex than just the counterintuitive parts, like Heisenberg uncertainty.
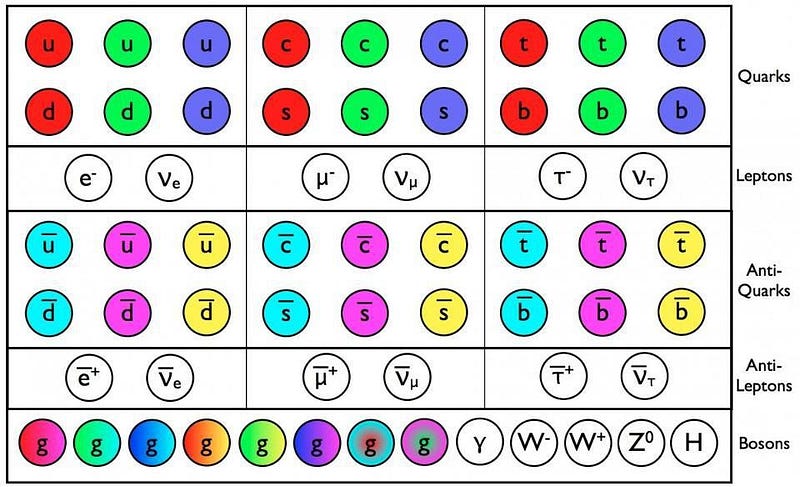
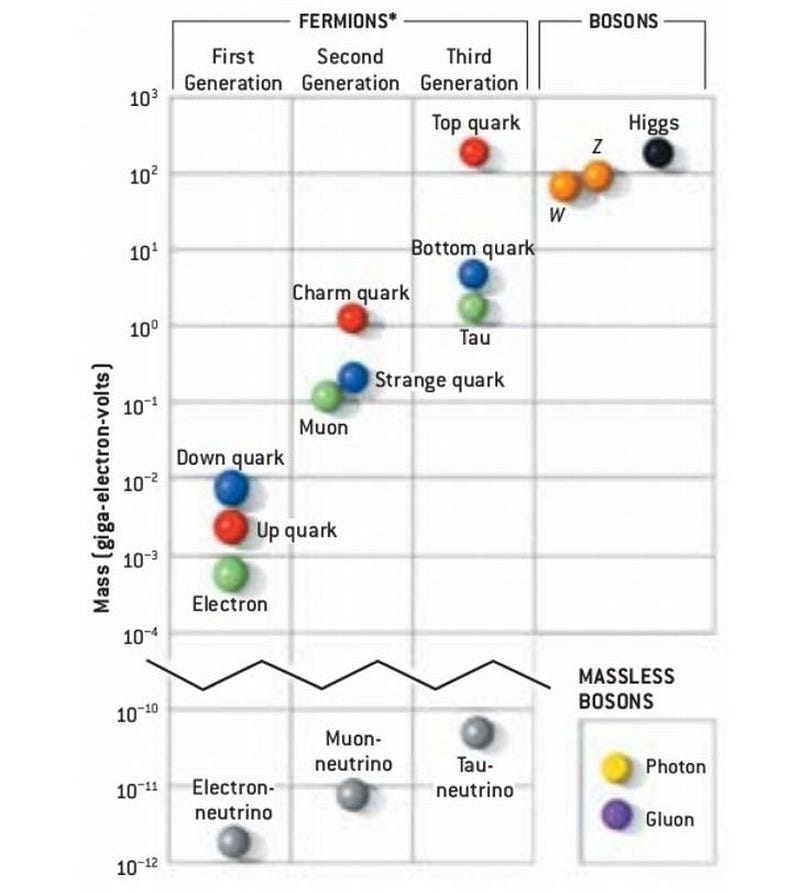
The Universe is made up of quanta, which are those components of reality that cannot be further divided into smaller components. The most successful model of those smallest, fundamental components that compose our reality come to us in the form of the creatively-named Standard Model.
In the Standard Model, there are two separate classes of quanta:
- the particles that make up the matter and antimatter in our material Universe, and
- the particles responsible for the forces that govern their interactions.
The former class of particles are known as fermions, while the latter class are known as bosons.
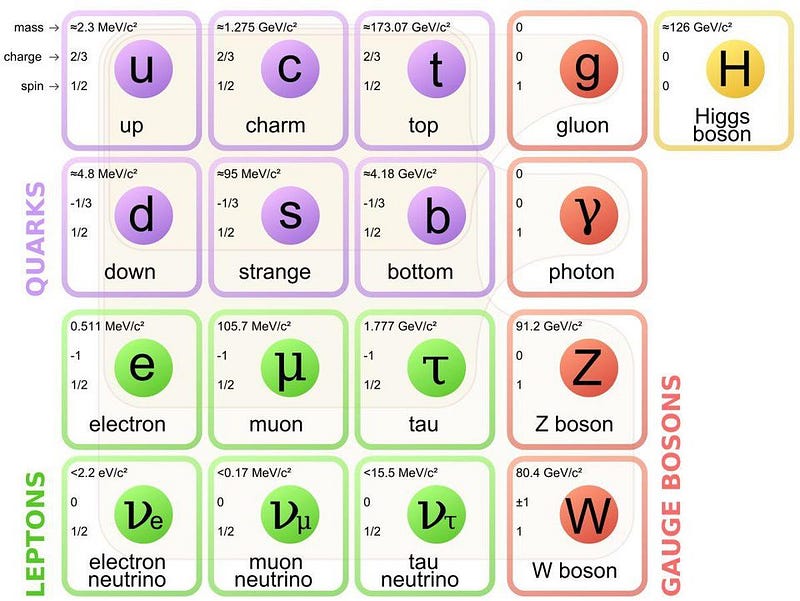
Even though, in the quantum Universe, many properties have an intrinsic uncertainty to them, there are some properties that we can know exactly. We call these quantum numbers, which are conserved quantities in not only individual particles, but in the Universe as a whole. In particular, these include properties like:
- electric charge,
- color charge,
- magnetic charge,
- angular momentum,
- baryon number,
- lepton number,
- and lepton family number.
These are properties that are always conserved, as far as we can tell.
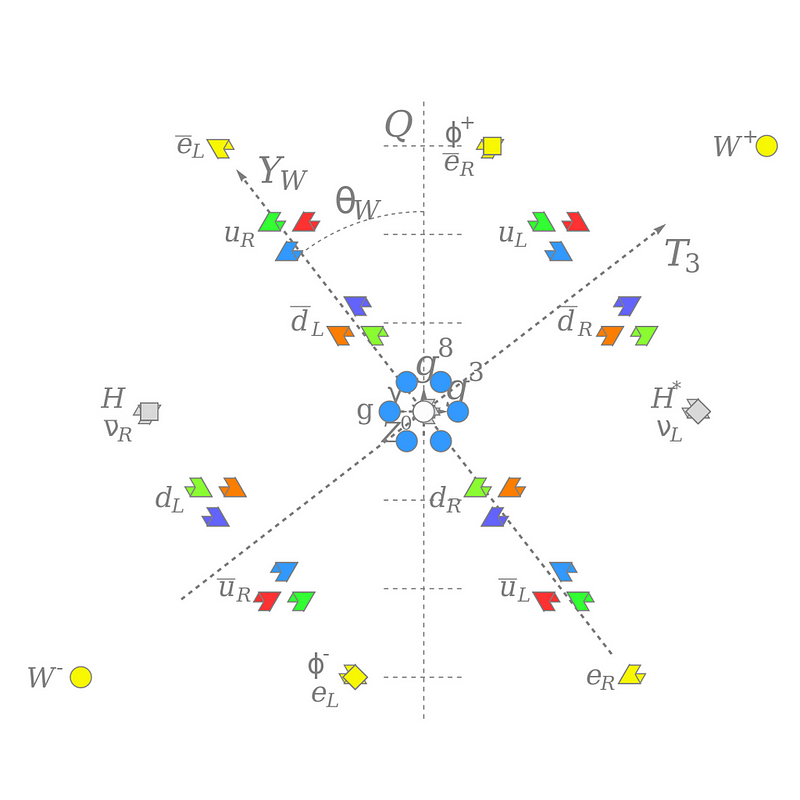
In addition, there are a few other properties that are conserved in the strong and electromagnetic interactions, but whose conservation can be violated by the weak interactions. These include
- weak hypercharge,
- weak isospin,
- and quark flavor numbers (like strangeness, charm, bottomness, or topness).
Every quantum particle that exists has specific values for these quantum numbers that are allowed. Some of them, like electric charge, never change, as an electron will always have an electric charge of -1 and an up quark will always have an electric charge of +⅔. But others, like angular momentum, can take on various values, which can be either +½ or -½ for an electron, or -1, 0, or +1 for a W-boson.
The particles that make up matter, known as the fermions, all have antimatter counterparts: the anti-fermions. The bosons, which are responsible for the forces and interactions between the particles, are neither matter nor antimatter, but can interact with either one, as well as themselves.
The way we view these interactions is by exchanges of bosons between fermions and/or anti-fermions. You can have a fermion interact with a boson and give rise to another fermion; you can have a fermion and an anti-fermion interact and give rise to a boson; you can have an anti-fermion interact with a boson and give rise to another anti-fermion. As long as you conserve all the total quantum numbers you are required to conserve and obey the rules set forth by the Standard Model’s particles and interactions, anything that is not forbidden will inevitably occur with some finite probability.
It’s important, before we enumerate what all the properties of the electron are, to note that this is merely the best understanding we have today of what the Universe is made of at a fundamental level. We do not know if there is a more fundamental description; we do not know if the Standard Model will someday be superseded by a more complete theory; we do not know if there are additional quantum numbers and when they might be (or might not be) conserved; we do not know how to incorporate gravity into the Standard Model.
Although it should always go without saying, it warrants being stated explicitly here: these properties provide the best description of the electron as we know it today. In the future, they may turn out to be an incomplete description, or only an approximate description of what an electron (or a more fundamental entity that makes up our reality) truly is.
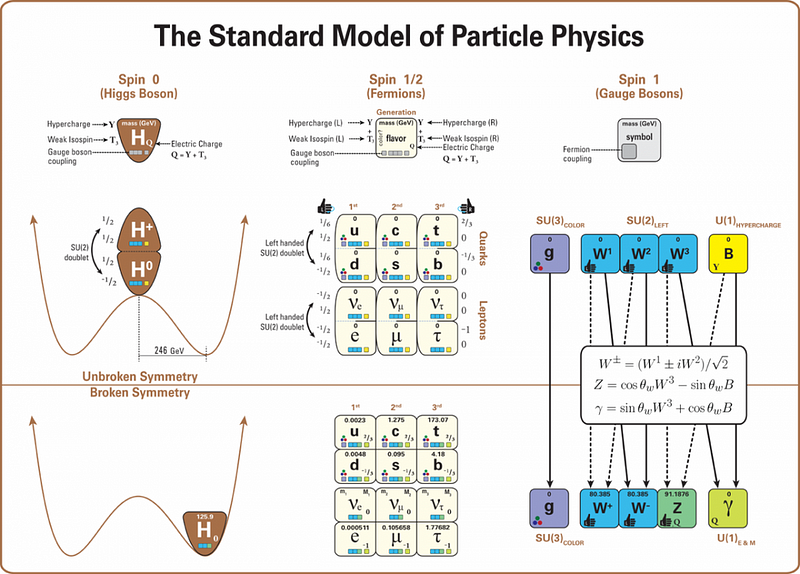
With that said, an electron is:
- a fermion (and not an antifermion),
- with an electric charge of -1 (in units of fundamental electric charge),
- with zero magnetic charge
- and zero color charge,
- with a fundamental intrinsic angular momentum (or spin) of ½, meaning it can take on values of +½ or -½,
- with a baryon number of 0,
- with a lepton number of +1,
- with a lepton family number of +1 in the electron family, 0 in the muon family and 0 in the tau family,
- with a weak isospin of -½,
- and with a weak hypercharge of -1.
Those are the quantum numbers of the electron. It does couple to the weak interaction (and hence, the W and Z bosons) and the electromagnetic interaction (and hence, the photon), and also the Higgs boson (and hence, it has a non-zero rest mass). It does not couple to the strong force, and therefore cannot interact with the gluons.

If an electron and a positron (which has some of the same quantum numbers and some quantum numbers which are opposites) interact, there are finite probabilities that they will interact through either the electromagnetic or the weak force.
Most interactions will be dominated by the possibility that electrons and positrons will attract one another, owing to their opposite electric charges. They can form an unstable atom-like entity known as positronium, where they become bound together similar to how protons and electrons bind together, except the electron and positron are of equal mass.
However, because the electron is matter and the positron is antimatter, they can also annihilate. Depending on a number of factors, such as their relative spins, there are finite probabilities for how they will decay: into 2, 3, 4, 5, or greater numbers of photons. (But 2 or 3 are most common.)
When you subject an electron to an electric or magnetic field, photons interact with it to change its momentum; in simple terms, that means they cause an acceleration. Because an electron also has a rest mass associated with it, courtesy of its interactions with the Higgs boson, it also accelerates in a gravitational field. However, the Standard Model cannot account for this, nor can any quantum theory we know of.
Until we have a quantum theory of gravity, we have to take the mass and energy of an electron and put it into General Relativity: our non-quantum theory of gravitation. This is sufficient to give us the correct answer for every experiment we’ve been able to design, but it’s going to break down at some fundamental level. For example, if you ask what happens to the gravitational field of a single electron as it passes through a double slit, General Relativity has no answer.
Electrons are incredibly important components of our Universe, as there are approximately 1080 of them contained within our observable Universe. They are required for the assembly of atoms, which form molecules, humans, planets and more, and are used in our world for everything from magnets to computers to the macroscopic sensation of touch.
But the reason they have the properties they do is because of the fundamental quantum rules that govern the Universe. The Standard Model is the best description we have of those rules today, and it also provides the best description of the ways that electrons can and do interact, as well as describing which interactions they cannot undergo.
Why electrons have these particular properties is beyond the scope of the Standard Model, though. For all that we know, we can only describe how the Universe works. Why it works the way it does is still an open question that we have no satisfactory answer for. All we can do is continue to investigate, and work towards a more fundamental answer.
Send in your Ask Ethan questions to startswithabang at gmail dot com!
Ethan Siegel is the author of Beyond the Galaxy and Treknology. You can pre-order his third book, currently in development: the Encyclopaedia Cosmologica.