Ask Ethan: Does A Time-Stopping Paradox Prevent Black Holes From Growing?

From outside a black hole, all masses take an infinite amount of time to cross the event horizon. How, then, can black holes grow?

Every Milky Way-sized galaxy should contain hundreds of millions of black holes, formed mostly from the deaths of the most massive stars. At the centers of these galaxies, supermassive black holes have devoured enough matter to grow to millions or billions of times the Sun’s mass, where sometimes they’re caught in the act of feeding on matter, emitting radiation and relativistic jets in the process. But, from the outside, any infalling mass would appear to take an infinite time to fall in; does that prevent black holes from growing? Olaf Schlüter wants to know, asking:

[F]or any object falling into a black hole, time slows down upon approach and comes to a standstill as the object reaches the event horizon. Reaching and passing that border would take an infinite amount of time measured by a distant observer… if ‘eating’ matter would take infinite time… how could supermassive black holes come into existence?

It sounds like a paradox, but relativity explains how it all really happens.

When you think about a black hole, there are two very different ways you can do it. The first way is to consider it from the point of view of an outside, external observer: to picture a black hole the way someone like us would see it. From this perspective, a black hole is simply a region of space where enough mass is contained within a given volume that the escape velocity — or the speed you’d need to achieve to break free from its gravitational pull — exceeds the speed of light.

Outside of that particular region, space may be severely bent, but particles that move or accelerate quickly enough, as well as light itself, can both propagate to any arbitrary location in the Universe. However, inside that region, there is no escape, with the border between inside and outside defined as the black hole’s event horizon.

The second way to think about a black hole, however, is from the perspective of a particle — whether massive or massless — that crosses the event horizon from outside to inside, and therefore falls into the black hole. From outside the event horizon, the infalling entity sees the outside Universe as well as the blackness of the event horizon, which grows larger and larger as they approach it.

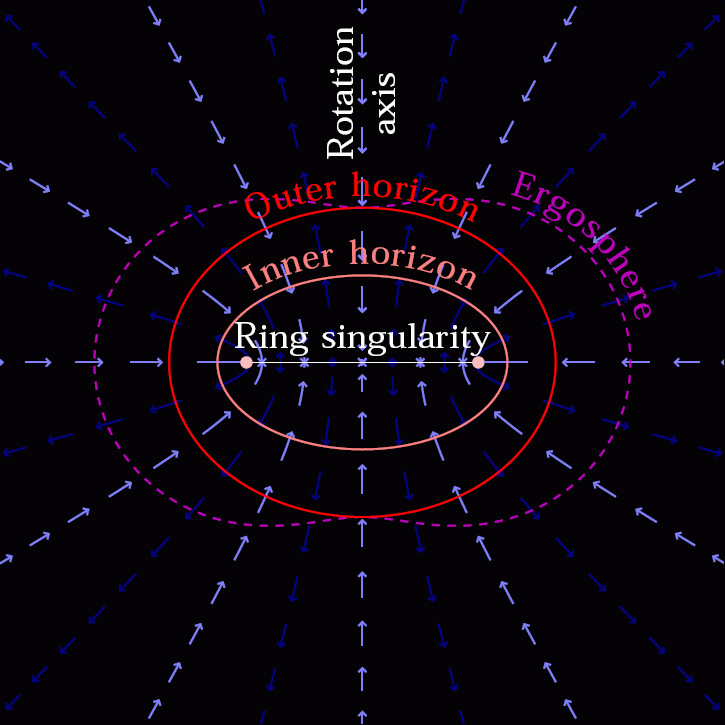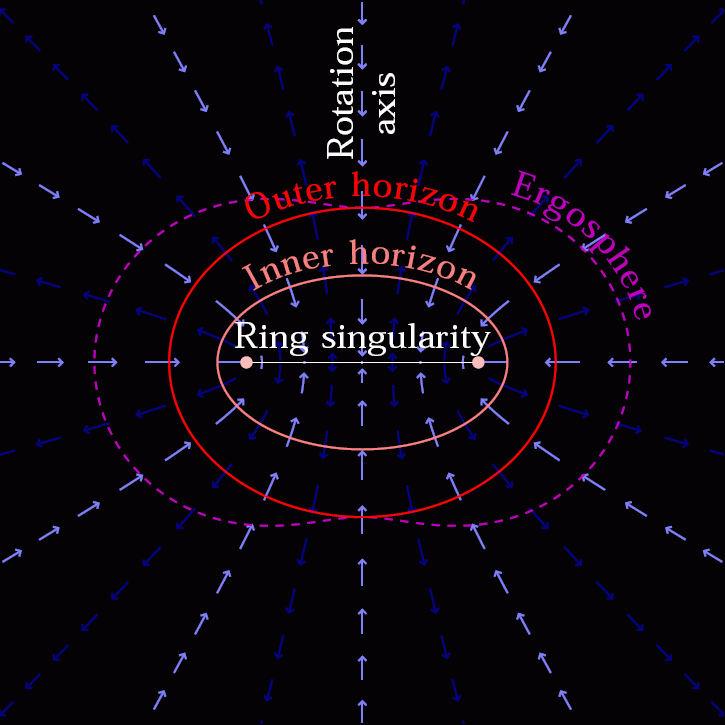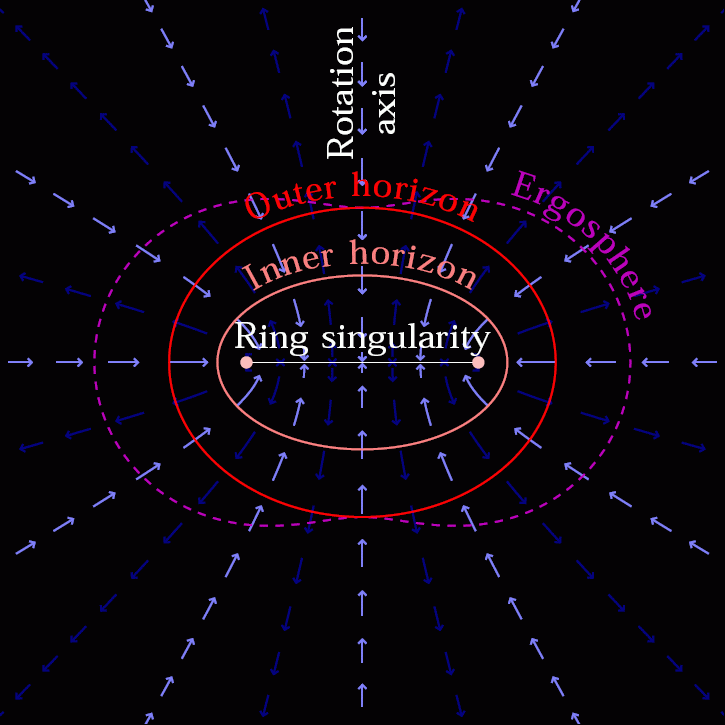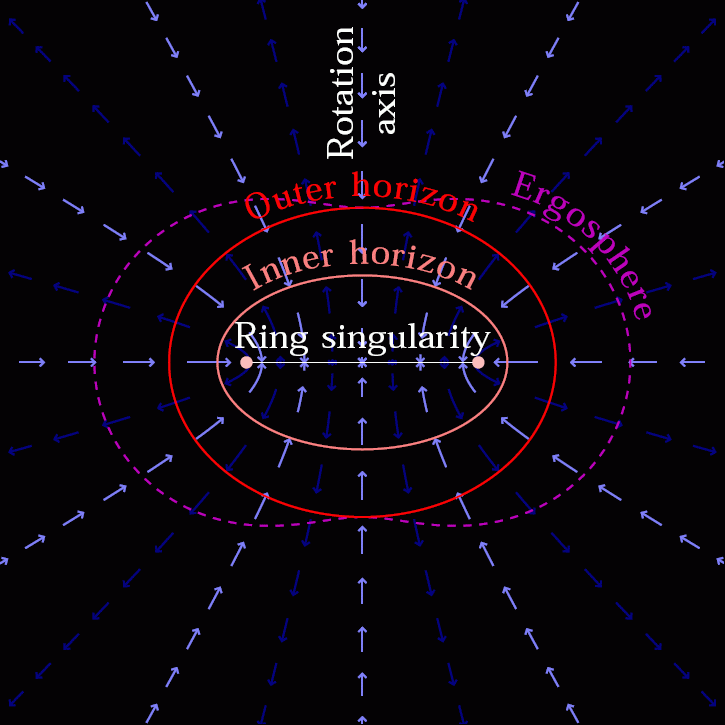
But once they cross the event horizon, something funny happens. No matter which direction they move or accelerate in, no matter how quickly or how powerfully they do so, they will always inevitably find themselves headed towards a central singularity. The singularity is either a zero-dimensional point (for non-rotating black holes) or a one-dimensional ring (for rotating black holes), and it cannot be avoided once the event horizon is crossed.

It’s important not to mix these perspectives up or conflate them with one another. Although they are both valid, it isn’t really possible to do a simple transformation from one point of view to the other. The reason is simple: from outside the black hole, you can never gain any information about what’s going on interior the event horizon, while from inside the black hole, you can never send any information to the outside.

And yet, particles — containing energy, angular momentum, and possibly charge — really do fall into black holes, increase their mass, and cause those black holes to grow. To understand exactly how this happens, we need to look at the problem from both perspectives independently, and only then can we see how to reconcile the seemingly paradoxical aspects of this puzzle.

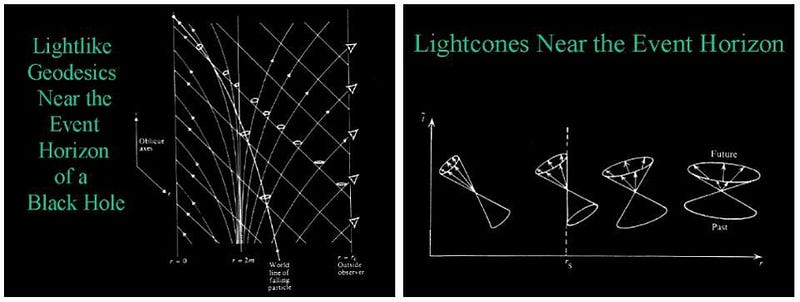
The physics is a little bit easier to understand if we view it from the perspective of the infalling particle. If the particle, existing in the curved space that’s presence in the vicinity of a pre-existing black hole, finds itself on a trajectory that will cross the event horizon, there’s a clear before-and-after scenario.

Before it crosses the event horizon, the black hole has a particular mass, spin, and event horizon radius, while the infalling particle also adds a slight deformation to the space it occupies. When it crosses over to the inside of the event horizon, its mass and angular momentum now add an supplementary contribution to the black hole’s previous parameters, causing the event horizon to grow. From the perspective of the infalling particle itself, everything makes clear sense.

But from the perspective of the outside observer, things are more challenging. Space is more severely curved the closer you get to the event horizon of a black hole, and since Einstein’s relativity links space with time, this means effects like gravitational redshift and gravitational time dilation become more and more pronounced the closer an infalling particle gets to that horizon.

In other words, for an outside observer who sees matter falling into a black hole, it will appear as though the material:

• takes on a redder color (as the photons get gravitationally redshifted),
• falls in slower and slower as it asymptotically approaches the event horizon (due to time dilation),
• appears fainter and fainter over time (as the number of photons per “amount-of-dilated-time” progressively decreases),
• and eventually gets “frozen” infinitesimally close to, but still outside, the event horizon.

From the perspective of an external observer, you could even argue that perhaps it’s impossible for black holes to grow. If any amount of material, no matter how massive, cannot cross over from outside the event horizon to inside the event horizon, how can a black hole ever become more massive?

Forget about growing into a supermassive one; it seems like it might not be possible for a black hole to even grow at all!

But we’ve tricked ourselves if this is our line of reasoning. Remember, from the perspective of an external observer, we can never gain any information about what’s occurring inside a black hole’s event horizon. While we can do theoretical calculations to determine what Einstein’s General Relativity predicts should be inside a black hole — where and with what properties we should find event horizons, ergospheres, singularities and more — an outside observer cannot acquire that information via any means.

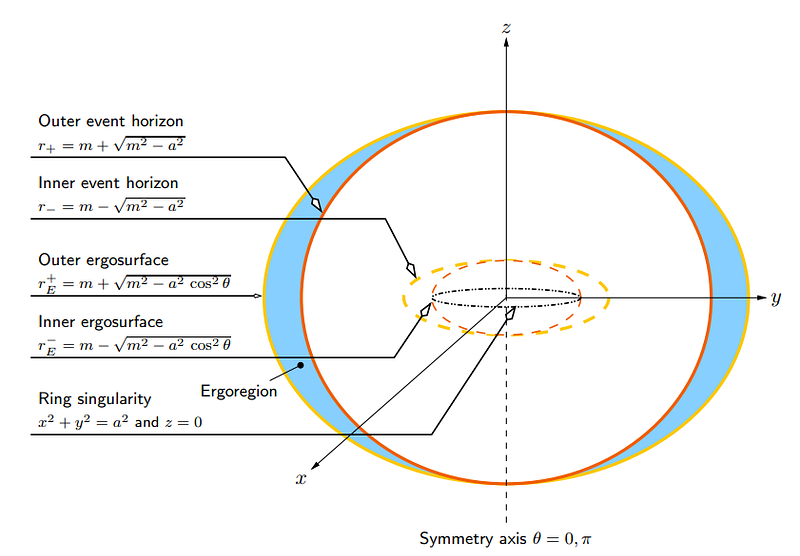
All that an external observer can ever perceive comes from outside the event horizon, and that’s a clue that points at a deeper truth: the event horizon isn’t itself a place where physics breaks down (a true singularity), it’s simply a place where an external observer is “shielded” from gaining information about what happens inside (a coordinate singularity). This means that what an infalling observer experiences must be correct, at some level, for all observers. Somehow, black holes must really grow, and an external observer must be able to see that growth as well.

How can they see that growth, then, given this apparent paradox?

The key is to remember that, for an external observer, a black hole is simply a region of space with so much matter-and-energy (and angular momentum, charge, and anything else that defines a black hole) that light cannot escape from within that region. If we accept that simple definition, we can do a thought experiment that completely resolves this paradox. Imagine that we begin with a black hole of one solar mass, that doesn’t rotate, with an event horizon of the exact size that our Sun would be if it collapsed into a Schwarzschild black hole: a sphere of about 3 kilometers in radius.

Now, let’s take another one solar mass object — perhaps another star just like our Sun — and let’s allow it to fall in to this black hole.

What’s going to happen?

The material from the star will be:

• ripped apart,
• stretched and compressed by the tidal forces of the black hole,
• spread out over an enormous region of space,
• and will asymptotically approach the event horizon, with every particle getting infinitesimally close to — but never crossing — the original event horizon.

The thing is, with an extra solar mass of material at just a little more than 3 kilometers away from the predicted central singularity, we now have two solar masses of material in this particular region of space. The event horizon of a two solar mass object is 6 kilometers in radius, meaning that all of this material is now inside the event horizon, after all!

That’s the resolution to this paradox: when matter falls onto a black hole, as seen by an outside observer, it only asymptotically approaches the event horizon. But since matter has mass, that mass is now contained within a critical volume of space, and that causes the new event horizon to now encompass the additional material that newly accumulated around the black hole.

It’s true that material from outside the black hole, even as it falls in on an inescapable trajectory, will never appear to cross the original event horizon from the perspective of an outside observer. But the more mass and energy a black hole accumulates, the larger the event horizon gets, and that means the newly infalling material can easily make inside the event horizon as it appears after that matter has made it to within a sufficiently small volume of space: close enough to the old enough event horizon to cause it to grow.

Black holes really do grow over time, and all observers can agree exactly when and by how much.

Send in your Ask Ethan questions to startswithabang at gmail dot com!