Ask Ethan: Could Gravitational Waves Ever Cause Damage On Earth?

Black hole mergers are some of the most energetic events in the Universe. Could the gravitational waves they produce ever harm us?

The Universe is not a static, stable place. Out of a vast collection of simple atoms, gas clouds collapse to form stars and planets, which then undergo their own individual life cycles. The most massive stars will die in cataclysmic events such as supernovae, producing stellar remnants such as neutron stars and black holes. Many of these neutron stars and black holes will then inspiral and merge, releasing a tremendous amount of energy in the form of gravitational waves. The light and particles produced in this way are capable of causing damage here on Earth, but what about the gravitational waves themselves? That’s Brian Brettschneider’s question, as he asks:

The gravitational waves detected on Earth by LIGO traveled great distances and were quite weak per unit volume of space by the time they arrived. If they originated much closer to Earth, they would be more energetic from our perspective. What would the effect of energetic gravitational waves created locally be on nearby objects. I’m thinking of binary ~30 solar mass black holes merging. Would the gravitational waves be noticeable? Could they cause damage?

It’s a great question that’s stymied even some of history’s greatest minds.

General Relativity, our current theory of gravity, was first put forth by Albert Einstein in 1915. The very next year, 1916, Einstein himself derived an unexpected property of his theory: it allowed the propagation of a new type of radiation that was purely gravitational in nature. This radiation, today known as gravitational waves, had some properties that were easy to extract: they had no mass and traveled at the speed of gravity, which ought to equal the speed of light.

But what wasn’t apparent, at least not right away, was whether these waves were real, physical, energy-carrying phenomena, or whether they were a pure mathematical artifact that didn’t have any physical meaning. In 1936, Einstein and Nathan Rosen (of Einstein-Rosen bridge and EPR paradox fame) wrote a paper called, “Do gravitational waves exist?” In the paper, submitted to the journal Physical Review, they argued that no, they do not.

They contended that these gravitational waves were mathematical and didn’t physically exist, the same way that the “0” we infer to be on the end of a ruler doesn’t physically exist. Fortunately, the paper was rejected on the recommendation of the anonymous referee, who turned out to be the physicist Howard Robertson, whom cosmology fans might recognize as the “R” in the Friedmann-Lemaitre-Robertson-Walker metric.

Robertson, also based at Princeton, surreptitiously pointed out to Einstein the correct way to handle the error he had made, which flipped the conclusion. The gravitational waves that appeared in the resubmitted version, which was accepted in 1937 with a different title in a different journal, predicted physically real waves. Just as electromagnetism had light, a massless form of radiation that carried real energy, gravitation has a completely analogous phenomena: gravitational waves.

If these waves exist, are physically real, and also carry energy, then the important question becomes whether they can transfer that energy into matter, and if so, by what process. In 1957, the first American conference on General Relativity, now known as GR1, took place in Chapel Hill, North Carolina. In attendance were some titanic figures in the world of physics, including Bryce DeWitt, John Archibald Wheeler, Joseph Weber, Hermann Bondi, Cécile DeWitt-Morette, and Richard Feynman.

Although Bondi would quickly popularize a particular argument that arose from the conference, it was Feynman who came up with the line of reasoning we now call the sticky bead argument. If you imagine that you have a thin rod with two beads on it, where one is fixed but one can slide, the distance between the beads will change if a gravitational wave passes through it perpendicular to the rod’s direction.

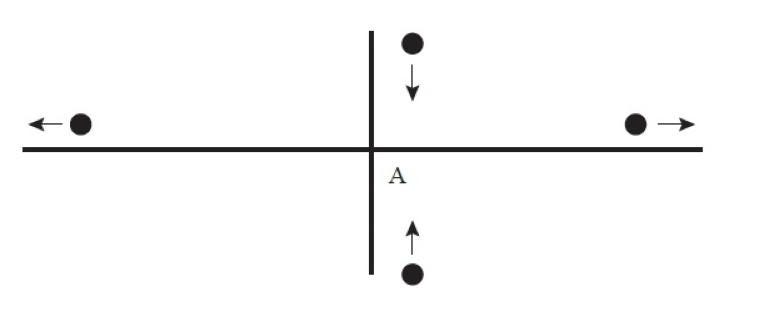
So long as the bead-and-rod are frictionless, there’s no heat produced, and the end state of the system consisting of the rod-and-beads is no different than before the gravitational wave passed through. But if there is friction between the rod and the bead that’s free to slide along it, that motion generates friction, which generates heat, which is a form of energy. Not only does Feynman’s argument demonstrate that gravitational waves do carry energy, but it shows how to extract that energy from the waves and put it into a real, physical system.

When a gravitational wave passes through the Earth, the same effects that it had on the bead-rod system would be at play. As the wave passed through the Earth, it would cause the directions perpendicular to the wave’s propagation to stretch-and-compress, alternately and in an oscillatory fashion, at 90 degree angles to one another.

Anything that was on the Earth that would be energetically affected by this motion of the space that it occupied would absorb that relevant amount of energy from the waves itself, and transform that energy into real, physical energy that would then be present on our world.

If we consider the first gravitational wave ever seen by LIGO — observed on September 14, 2015 but announced almost exactly 4 years ago today (on February 11, 2016) — it consisted of two black holes of 36 and 29 solar masses, respectively, that merged to produce a black hole of 62 solar masses. If you do the math, you’ll notice that 36 + 29 does not equal 62. In order to balance that equation, the remaining three solar masses, corresponding to approximately 10% of the mass of the smaller black hole, needed to get converted into pure energy, via Einstein’s E = mc². That energy travels through space in the form of gravitational waves.

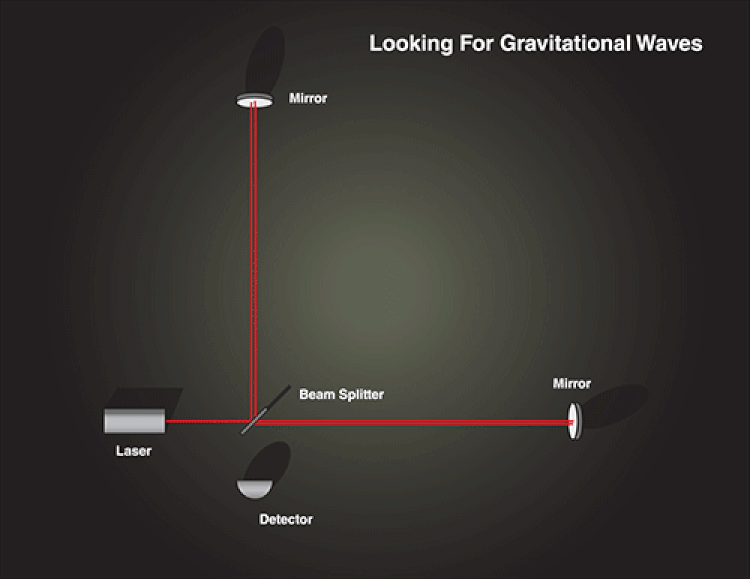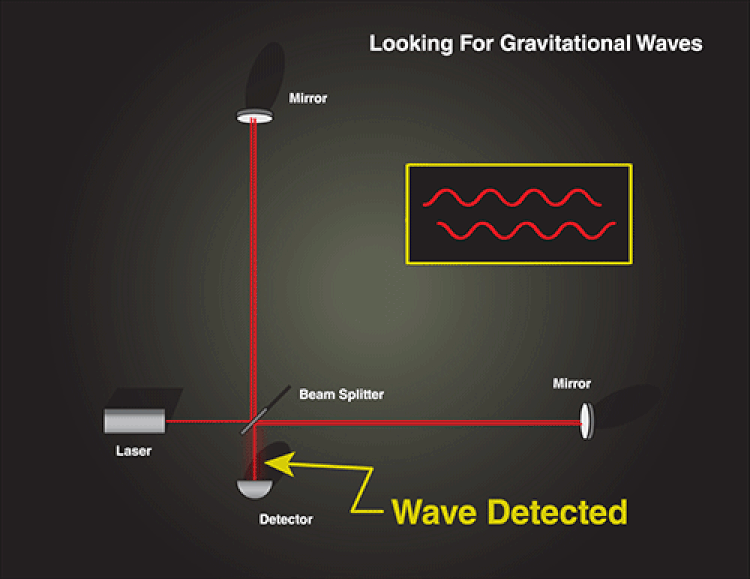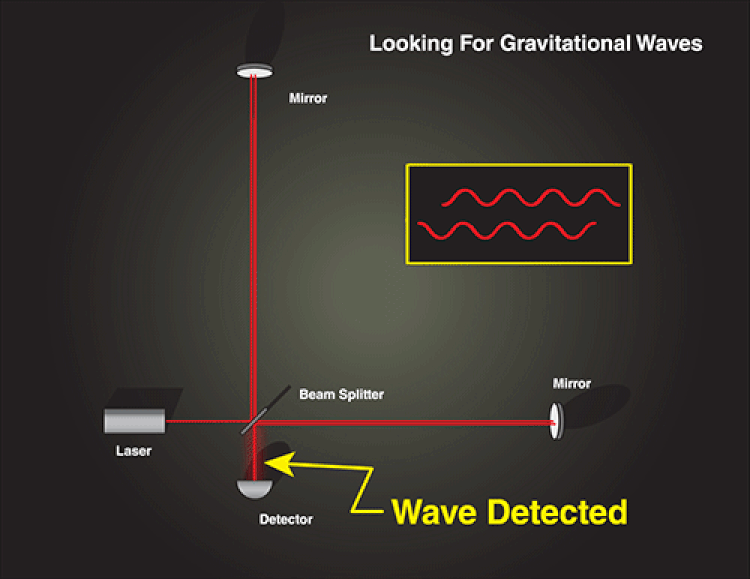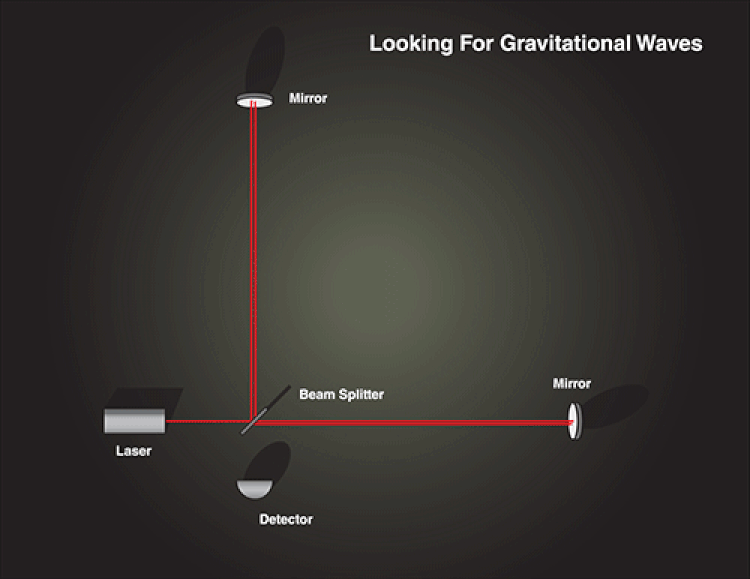
After a journey of about 1.3 billion light-years, the signal from those merging black holes arrived on Earth, where they passed through our planet. A tiny, tiny fraction of that energy was deposited into the twin LIGO detectors at Hanford, WA, and Livingston, LA, causing the lever arms that house the mirrors and laser cavities to alternately increase-and-decrease in length. That tiny bit of energy, extracted by an apparatus that humans built, was enough to detect our first gravitational waves.

There is an enormous amount of energy emitted when two black holes of masses comparable to these merge; converting three solar masses worth of material into pure energy over a timescale of just 200 milliseconds is more energy than all the stars in the Universe give off, combined, over that same amount of time. All told, that first gravitational wave contained 5.3 × 10⁴⁷ J of energy, with a peak emission, in the final milliseconds, of 3.6 × 10⁴⁹ W.

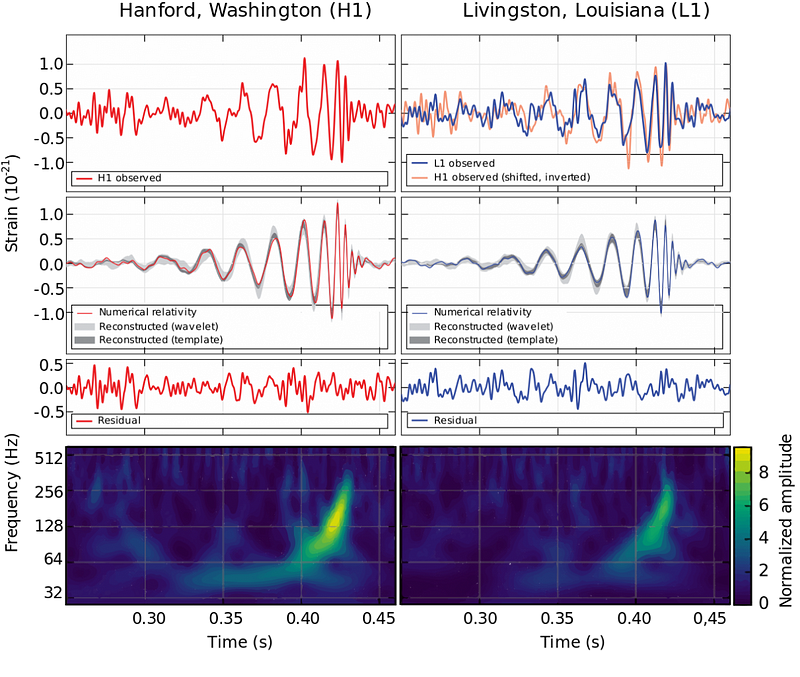
But from over a billion light-years away, we saw only a tiny, minuscule fraction of that energy. Even if we consider all of the energy received by the entire planet Earth from this gravitational wave, it only comes out to 36 billion J, the same as the amount of energy released by:

• burning through six barrels (about 1000 L) of crude oil,
• sunlight shining on the island of Manhattan for a duration of 0.7 seconds,
• 10,000 kWh of electricity, the average annual electricity consumption of an American household.

The energy emitted from a source in space always spreads out like the surface of a sphere, meaning that if you were to halve the distance between yourself and these merging black holes, the energy you’d receive would quadruple.

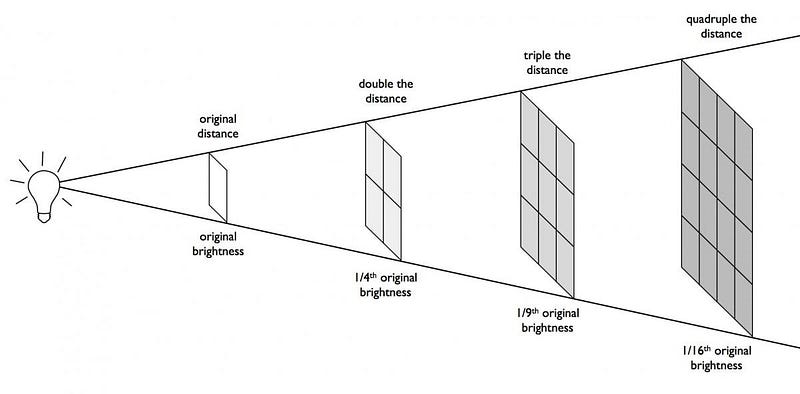
If instead of 1.3 billion light-years, these black holes merged just 1 light-year away, the strength of these gravitational waves that hit Earth would equate to about 70 octillion (7 × 10²⁸) joules of energy: as much energy as the Sun produces every three minutes.

But there’s one important way that gravitational waves and electromagnetic radiation (like sunlight) differ. Light is easily absorbed by normal matter, and imparts energy into it based on the interactions of its quanta (photons) with the quanta we’re made out of (protons, neutrons and electrons). But gravitational waves mostly pass right through normal matter. Yes, they cause it to alternately expand-and-contract in mutually perpendicular directions, but the wave largely passes through the Earth unaffected. Only a small amount of energy gets deposited, and there’s a subtle reason why.

When a gravitational wave gets emitted, its energy spreads out proportional to the distance squared. But the amplitude of a gravitational wave — the thing that determines by how much matter will expand-and-contract — only falls off linearly with the distance. When the first black hole-black hole merger we ever saw the gravitational waves from passed through Earth, our planet contracted-and-expanded by about the width of a dozen protons, all lined up together.

If those same black holes had merged at a distance of 1 light-year, Earth would have stretched-and-compressed by about 20 microns. If they had merged at the same distance Earth is from the Sun, the entire planet would have stretched-and-compressed by about 1 meter (3 feet). For comparison, that’s about the same amount of stretching-and-compressing that happens every day due to the tidal forces created by the Moon. The biggest difference is that it would happen much faster: with stretching-and-compressing on the timescale of milliseconds, rather than ~12 hours.

There are some ways that a large-enough amplitude gravitational wave could meaningfully impart energy to Earth. Crystals packed in intricate lattices would heat up all throughout the Earth’s interior, potentially cracking or shattering if the gravitational wave is strong enough. Earthquakes would ripple throughout our planet, cascading and overlapping, causing worldwide damage on our surface. Geysers would erupt spectacularly and irregularly, and it’s possible that volcanic eruptions would be triggered. Even the oceans would produce global tsunamis, disproportionately affecting coastal areas.

But a black hole-black hole merger would need to take place within our Solar System for that to happen. From even the distance of the nearest star, gravitational waves would pass through us almost completely unnoticed. Although these ripples in spacetime carry more energy than any other cataclysmic event, the interactions are so weak that they barely affect us. Perhaps the most remarkable fact of all is that we’ve actually learned how to successfully detect them.

Send in your Ask Ethan questions to startswithabang at gmail dot com!