10 profound answers about the math behind AI

Why do machines learn? Even in the recent past, this would have been a ridiculous question, as machines — i.e., computers — were only capable of executing whatever instructions a human programmer had programmed into them. With the rise of generative AI, or artificial intelligence, however, machines truly appear to be gifted with the ability to learn, refining their answers based on continued interactions with both human and non-human users. Large language model-based artificial intelligence programs, such as ChatGPT, Claude, Gemini and more, are now so widespread that they’re replacing traditional tools, including Google searches, in applications all across the world.

How did this come to be? How did we so swiftly come to live in an era where many of us are happy to turn over aspects of our lives that traditionally needed a human expert to a computer program? From financial to medical decisions, from quantum systems to protein folding, and from sorting data to finding signals in a sea of noise, many programs that leverage artificial intelligence (AI) and machine learning (ML) are far superior at these tasks compared with even the greatest human experts.

In his new book, Why Machines Learn: The Elegant Math Behind Modern AI, science writer Anil Ananthaswamy explores all of these aspects and more. I was fortunate enough to get to do a question-and-answer interview with him, and here are the 10 most profound responses he was generous enough to give.

Anil Ananthaswamy’s new book, Why Machines Learn: The Elegant Math Behind Modern AI, highlights the life-altering technologies that are driving the AI/ML boom, as well as the mathematics that underpins it all.

Ethan Siegel (ES): Many people hear the term “AI” (for artificial intelligence) and immediately think that something much, much deeper and fancier is going on than, say, what they think of when they hear the term “a computer program.” What would you say are the main differences and similarities between a traditional computer program and a piece of computer software that incorporates artificial intelligence into it?

Anil Ananthaswamy (AA): When we talk of AI these days, it’s a particular form of it, called machine learning (ML). Such systems are, of course, computer programs too. But unlike a traditional computer program, where the programmer knows the exact algorithm to implement and turn some input into the requisite output, machine learning programs figure out the algorithm that turns inputs into outputs, by examining patterns that exist in training data. Computer software that incorporates AI would use such ML programs. The strength of ML lies in its ability to learn complex algorithms to transform inputs (say, a text prompt describing an image) into outputs (the image)—programmers would find it near impossible to explicitly engineer such algorithms; they have to be learned from patterns that exist in data.

This graphical hierarchy of mathematical spaces goes from the most general type of space, a topological space, to the most specific: an inner product space. All metrics induce a topology, but not all topological spaces can be defined by a metric; all normed vector spaces induce a metric, but not all metrics contain normed vector space; all inner product spaces induce a norm, but not all normed vector spaces are inner product spaces. Mathematical spaces play a vital role in the math powering artificial intelligence.

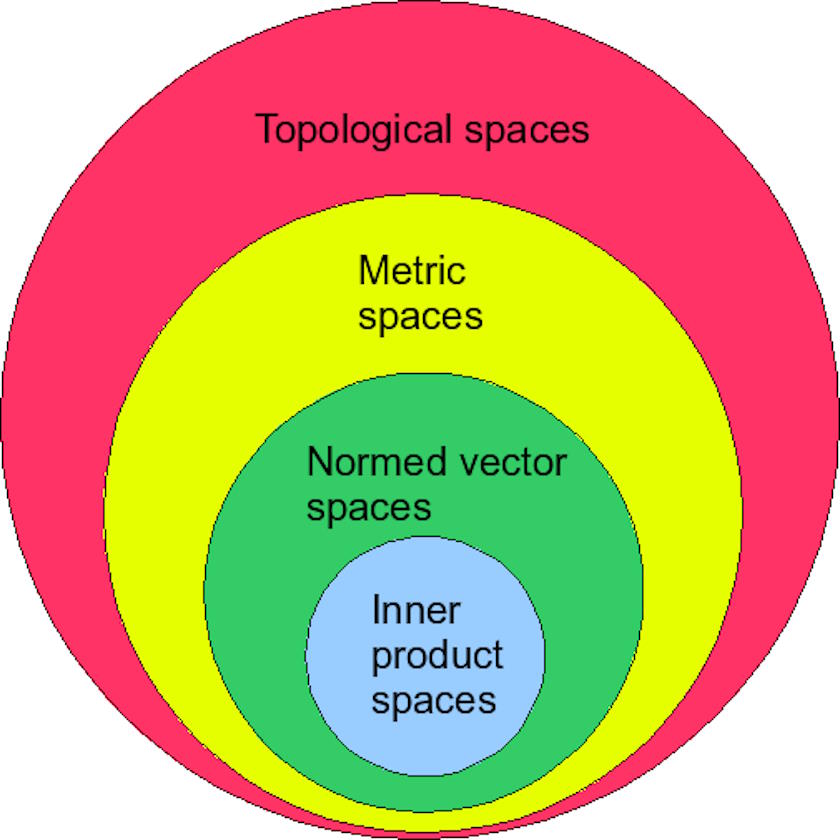
ES: Your book is called “Why Machines Learn: The Elegant Math Behind Modern AI,” and I was initially puzzled by the description of the math behind modern AI being called elegant. Most of the math that AI leverages, at least as I understand it, is simply the math that a math or physics major learns in their first two years of undergraduate education: multidimensional calculus, linear algebra, probability and statistics, Fourier analysis, plus a little bit of information theory and (sometimes) differential equations. What’s so “elegant” about these mathematical tools?

AA: The elegance of the mathematics that underpins machine learning is, of course, subjective. I speak of elegance from the perspective of ML theorems and proofs. For example, the convergence proof of Frank Rosenblatt’s perceptron algorithm, which shows that the algorithm will find a way to linearly separate two clusters of data, if such a linear divide exists, in finite time, is beautiful. So are the ideas behind machine learning algorithms called support vector machines, which use so-called kernel methods to project low dimensional data into higher, even infinite, dimensions, and compute dot products of vectors in the higher dimensional space using their low-dimensional counterparts, making it computationally tractable. The backpropagation algorithm used to train deep neural networks is elegant in its simplicity—and it’s a straightforward application of the chain rule in calculus. There are many other such examples.

This illustration of a human brain was generated by DALL-E, a generative AI program, in late 2023. Although it bears many superficial resemblances to a human brain, it lacks many of the brain’s defining structures and presents a fundamentally unrealistic pattern of neurons, glial cells, and folding properties. However, it was by considering the brain that artificial neural networks, the backbone of generative AI, was first developed.

ES: We often use terms like “artificial intelligence” and “machine learning” synonymously, and when we do, we’re compelled to draw parallels between “natural intelligence” and “learning” the way we, as intelligent, knowledge-seeking humans, understand them. But our traditional ideas of “intelligence” and “learning” don’t necessarily reflect what the AI/ML systems are doing behind the scenes. What’s a more accurate description behind what an artificial intelligence system actually does?

AA: Modern artificial intelligence is indeed synonymous with machine learning, in particular, deep learning, which is a form of ML. Broadly speaking, these ML algorithms learn about patterns that exist in data, without being explicitly programmed to do so. The algorithms are often used to discriminate between different classes of data (say, for image or voice recognition), or they are used to generate new data by learning and sampling from probability distributions over the training data. In the latter case, if the algorithm learns such distributions, then it can be trained to sample from the distribution to generate data that is statistically similar to the training data, hence the name generative AI.

Large language models are an example of generative AI. While these algorithms can be extremely powerful and even outdo humans on the narrow tasks they are trained on, they don’t generalize to questions about data that falls outside the training data distribution. In that sense, they are not intelligent in the way humans are considered intelligent.

A pixelated image of Earth, which is a simulated view of what a telescope located 547 astronomical units from the Sun and outfitted with a coronagraph would see in an exoplanetary system, using the Sun’s gravity to gravitationally enhance and magnify a potentially inhabited Earth-sized world. Each pixel in this image could be converted into a one-dimensional vector, and it would require approximately a 10,000-dimensional vector to encode the full image.

ES: One of the biggest tasks assigned to AI falls into what humans might describe as “pattern recognition.” This is something our brains do instinctively and by default: we make decisions about our current experience based on what we’ve experienced in the past. For a computer, however, pattern recognition only arises when there’s a sufficient mathematical match between something that gets fed into a computer and something that the system has already “seen” as part of its training data set. How does a computer accomplish this task of pattern recognition, which was previously so elusive before AI came onto the scene?

AA: Elaborating on the answer to the previous question, most ML algorithms do pattern recognition by first converting data into vectors. For example, a 10×10 image can be turned into a 100-dimensional vector, where each dimension records the value of one pixel. Once mapped into this space, an algorithm can do multiple things. It can, for instance, find a high-dimensional surface that separates one cluster of vectors representing images of cats from another cluster of vectors representing images of dogs. Once it’s found such a surface, then the algorithm can be used to classify a previously unseen image as either that of a dog or a cat by converting the image into its vector, mapping the vector and checking if it falls on one or the other side of the surface.

In the case of generative AI, the algorithm can find or estimate a high-dimensional surface that represents the probability distribution over the data (in this case, the vectors representing images of cats and dogs). Having estimated that distribution, it can sample from the surface to find an underlying vector that can be turned back into an image that looks like a cat or a dog. Deep learning takes this process further, by identifying features that can be used to classify images (long, floppy ears are more likely to be associated with dogs, say), or to learn probability distributions over such features rather than individual pixel values.

With a large training data set, such as a large number of high-resolution faces, artificial intelligence and machine learning techniques can not only learn how to identify human faces, but can generate human faces with a variety of specific features. This crowd in Mauerpark, Berlin, would provide excellent training data for the generation of Caucasian faces, but would perform very poorly if asked to generate features common to African-American faces.

ES: I’ve often heard it said that the performance of any AI system is limited by the quality of the data that it’s trained on, as well as the quality of the data that is then fed into it for analysis. Even with what we call “generative” AI capabilities, we still don’t believe it’s true that AI can make creative leaps ex nihilo. How do the limitations of the original data set ultimately restrict what an AI system is capable of as far as generating what we perceive as “new” content?

AA: Training data will hew to some probability distribution, and there’s an assumption that this distribution represents the ground truth. For example, if you are learning about patterns in images of people, there’s an assumption that the hundreds of thousands of images you might be using is representative of all people, if not a great variety of them. Anything you ask of a machine learning system that has learned patterns that exist in some training data is limited to analyzing new data that is assumed to be drawn from the same distribution. So, if you trained your image recognition system only on faces of Caucasians, it won’t be able to generate an image of someone from China or India, because it never saw such patterns in the training data. These are inherent limitations of current machine learning systems.

Based on the Kepler lightcurve of the transiting exoplanet Kepler-1625b, we were able to infer the existence of a potential exomoon. The fact that the transits didn’t occur with the exact same periodicity, but that there were timing variations, was our major clue that led researchers in that direction. With large enough exoplanet data sets, machine learning algorithms can now find additional exoplanet and exomoon candidates that were unidentifiable with human-written algorithms.

ES: In the field of astrophysics, we’ve recently seen large sets of astrophysical data fed into machine learning systems that have subsequently uncovered hundreds or even thousands of objects — galaxies, exoplanets, protoplanetary systems, etc. — that humans had either overlooked or hadn’t been able to find when they first looked through the data. How do AI/ML systems accomplish these tasks, and what makes them so ideally suited to capture these details that are “hiding” in the data, where even the highest-expertise humans miss them?

AA: There’s no magic here. This comes down to the strength of these AI/ML algorithms at finding subtle differences between categories of objects, given enough high-quality data: differences humans might miss. Add to that the speed and memory capacity of modern computing systems, and these algorithms can indeed uncover at scale new objects in astrophysical data. But there’s always the danger that ML algorithms can overfit—picking up on spurious correlations between data and their categories—and thus make errors that humans might not. Much of machine learning comes down to avoiding such overfitting, such that the algorithm performs optimally on unseen data.

A screenshot from a query about integers directed to iask.ai, along with its woefully incorrect response. The correct answer is -5, which requires inputting several additional prompts to coax the AI into the correct response.

ES: Most people are familiar with AI systems largely through large language models (LLMs) like ChatGPT, Claude, or Gemini. Even though these models can hold conversations with humans and deliver very confident, informative answers to practically any query you can imagine — including reading and deciphering CAPTCHAs, which traditional computers are notoriously bad at — the information contained within many of those answers is often incorrect. For instance, if I ask one of these models, “What is the smallest integer whose square falls between 15 and 26?” I’m practically guaranteed to see an AI system fail miserably, despite its confidence in its answer. What limitation are we running up against: one of math, one of training data, one of comprehension, or is there something else at play entirely?

AA: Large language models have been trained to predict the next word, given some sequence of words (using “words” instead of “tokens” here). Imagine an LLM that has been trained to predict the next word using much of the text on the Internet, particularly good quality text like Wikipedia. Now, when given some sequence of 100 words, the LLM generates the 101st word, the 102nd word and so on, until it generates a token symbolizing end-of-text. It stops. Mathematically, at each step, the LLM is calculating the conditional probability distribution over its entire vocabulary given some input sequence of words, picking the most likely word from that distribution, appending it to the input sequence, and doing the same for this new input. It’s not specifically being taught to reason or answer math questions.

That an LLM can seemingly do some of these tasks, if it’s scaled up appropriately in size and amount of training data, was what surprised people. In situations where it can answer correctly, showing apparent comprehension, it means that it has seen enough training data to correctly model the conditional probability distributions in extremely high-dimensional space. So, depending on where you set the bar for what constitutes understanding or comprehension, LLMs can clear it comfortably or fail miserably. And they fail because the architecture of LLMs and their training is inherently about modeling correlations: it’s just that the size and scale of these systems is such that they can learn sophisticated correlations that are enough to answer a whole host of questions; and yet, they can fail on simple math and reasoning tasks.

It’s an open question whether simply making LLMs bigger will make them better at reasoning. Some think that it’s an in-principal limitation of LLMs and they’ll never be able to correctly reason all the time. Others think that scaling up will solve some of these problems, in much the same way that large LLMs can do things that smaller LLMs cannot, even though they are trained in exactly the same manner, only with more data to compute. The debate is raging.

This museum exhibit showcases Deep Blue: the computer that first defeated a reigning world chess champion in a chess match, defeating Garry Kasparov. Since Ruslan Ponomariov defeated Fritz in 2005, no human has defeated a top performing computer in a game of classical chess. Currently, the top-rated chess computers are rated 3200-3300: about 400 points higher than the greatest human chess players of all-time.

ES: In the past, we’ve seen computers far surpass what even the highest-expertise humans can accomplish. This happened back in the 1990s (or, arguably, even earlier) for games like Checkers, Othello, and Chess, and later, for much more complicated games, like Go, in 2015. Today, many people fully expect that generative AI systems will someday surpass human capabilities in all realms of life, from art and music and filmmaking to theoretical physics and pure mathematics. On the other hand, others scoff at that idea, and insist that humans will not only always have a place in those arenas, but that any type of AI will never be able to equal what the best humans can do. Based on what you understand about AI, what are your thoughts on that topic?

AA: I doubt that current deep learning systems, even those trained as generative AIs, will surpass humans in all realms of life. But that’s not to say that there won’t be innovations in the way these machine learning systems are architected and trained that might enable more powerful machines that approach the kind of flexible intelligence humans have. Remember that it took the invention of convolution neural networks, the use of GPUs and large amounts of training data to crack the image recognition problem. Similarly, the invention of the transformer architecture made LLMs possible. It would have been hard to foresee these developments before they happened.

In fact, before deep learning cracked the image recognition problem, many thought it was impossible. But it happened. I suspect that for an AI to display human-like intelligence, it will have to be embodied and learn through interactions with its environment (physical or virtual). Our intelligence is very much a consequence of brains that are embedded in bodies. It’s also true that evolution discovered the structure of our brains and bodies and there’s no in-principle reason to think that we might not be able to do so with machines. Exactly when and how is a matter of considerable debate.

This photograph of a high-performance computing center at the University of Stuttgart leverages an incredible amount of computing power, but requires the expenditure of a tremendous amount of electrical power for it to work. The recent rise of AI data centers, which need an enormous amount of power themselves. is another new addition to humanity’s need for electricity generation.

ES: One of the “dirty little secrets” of  generative AI systems is usually how much power and energy they require in order to answer even the most mundane of queries. Is this a problem that we expect to persist eternally, or can the same mathematical tools that AI leverages to generate its responses to queries be used to increase the efficiency of the AI systems that generate these answers?

AA: The power and energy required to train large language models and other forms of generative AI is indeed an extremely serious concern. There are, however, efforts underway to make artificial neural networks more efficient, by using so-called spiking neural networks, which use artificial neurons that “spike” in much the same way that biological neurons do, instead of being constantly on. Spiking neural networks have proven harder to train, because the threshold function that determines when a neuron should spike is not differentiable, and training a neural network using backpropagation requires the entire chain of computation to be differentiable, in order to calculate gradients for optimization.

But recent advances have shown how to calculate approximate gradients even for spiking neural networks, enabling their training. Such networks consume far less energy, but only if they run on neuromorphic chips that implement hardware rather than software neurons. There’s considerable work required to make all this possible at scale.

This photograph of a hologram at the MIT museum looks like a three-dimensional object, but is only a two-dimensional light field encoded onto the surface of a hologram. Holograms are lower-dimensional surfaces that encode information about the entire higher-dimensional object within the higher-dimensional space, in (as far as we can tell) a lossless fashion. Such dimensional reduction techniques could potentially have widespread applications, including for machine learning.

ES: Finally, there are plenty of fields of mathematics that are far more intricate and advanced than what a traditional AI/ML system leverages. How do you foresee the capabilities of AI/ML changing — hopefully to make them more powerful, more accurate, and more capable problem-solvers — based on what types of mathematics get incorporated into these “under the hood” engines?

AA: One way for machine learning systems to become more powerful, more accurate and more capable problem solvers is to leverage the patterns hidden in data in more sophisticated ways. One could, for example, use manifold learning, which assumes that extremely high-dimensional data (which are computationally expensive to work with) have low-dimensional structures: lowering the dimensionality of the data can make machine learning faster. Of course, manifold learning assumes that such dimensionality reduction is possible and doesn’t result in loss of information.

Another method for extracting more information from data without making too many such assumptions combines topological data analysis (which, so to speak, determines the shape or features of data present at global scales) and machine learning. Yet another method for squeezing more out of data is to use graph theory alongside machine learning. Graphs are sophisticated, combinatorial data structures that can be used to represent complex relationships between objects and provide an alternative to vectors; Combining graphs with machine learning promises to increase ML’s pattern recognition prowess.

Anil Ananthaswamy’s book, Why Machines Learn: The Elegant Math Behind Modern AI, came out on July 16, 2024, and is now available wherever books are sold.