Alexander Friedmann: a pioneer of cosmic expansion

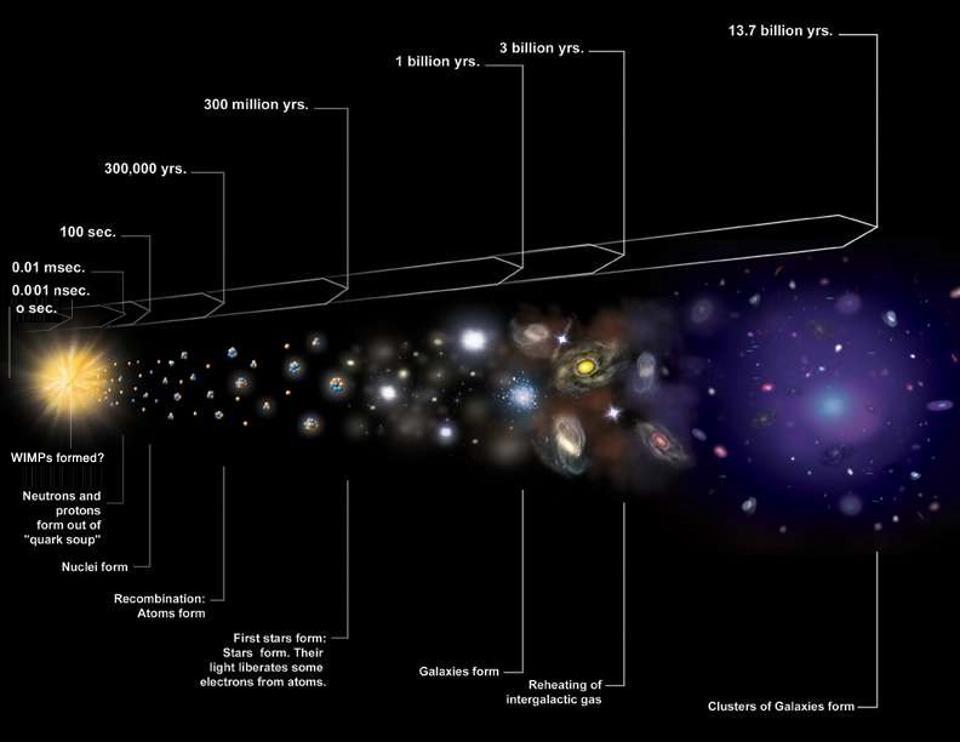
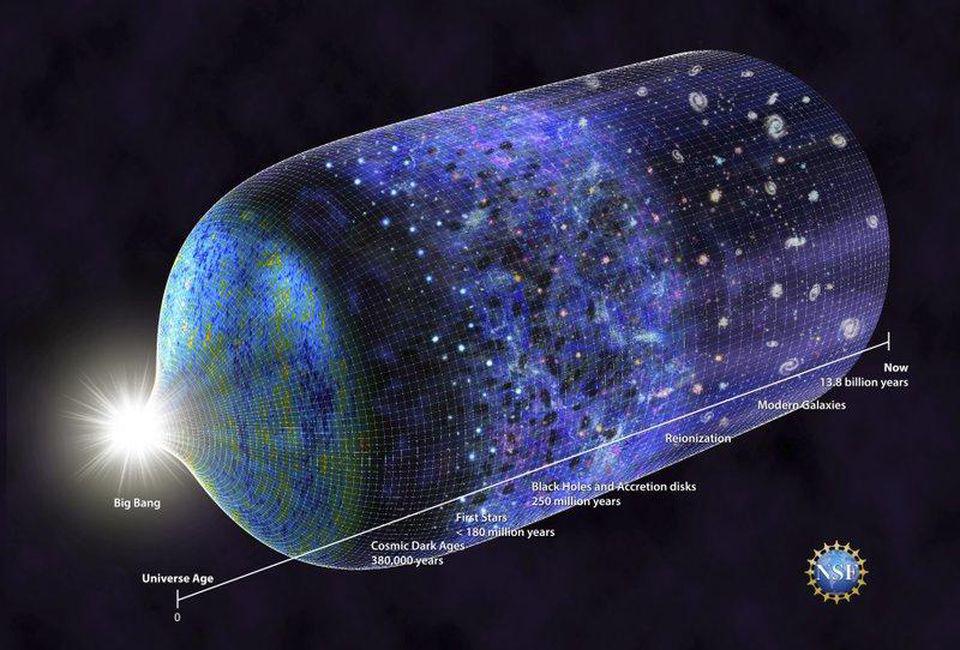
The expansion of the Universe is one of the most remarkable scientific findings of all time. It is also widely misunderstood, both conceptually and historically. Let’s take a look at both the concept and the history of cosmic expansion today.

Expansion is not like a bomb

When we say the universe is “expanding,” it is hard to avoid the image of a bomb that detonated a long time ago. The Big Bang is the “explosion,” and the galaxies that fly away from the exploding point are like shrapnel spreading outward in all directions from that central point. But that is not what the cosmic expansion means at all. If this image was accurate, space would be a static background, and the Universe would have a very special point, the center where the explosion originated. But there is no special point in the Universe. Cosmic geometry is very democratic, with all points being equal in the eyes of space.

The usual way this is explained is by picturing a balloon with coins glued to its surface. The balloon’s surface represents space (in two dimensions, which is easier to see), and the coins represent galaxies. As the balloon expands, the coins stay the same size but move away from one another. If you were a being in one galaxy, you would see all other galaxies moving away from you. But so would your neighbors as well as observers in any of the other galaxies. This is what is meant by the Universe not having a center. All points on the balloon are stretching away from one another. The expansion of space carries the galaxies (coins) away. This is an example of an expanding “closed” geometry, since the surface of the balloon is closed: if you start moving in one direction, you would get back to your starting point.

If you want a different way to picture this (one that I use in my teaching), imagine a classroom with desks resting on the floor. Then imagine I had a special button that would stretch the floor in two directions equally, north-south and east-west. If you were sitting at a desk, you would see the other desks moving away from you. And so would your classmates. No one desk is the center of this expansion. This is an example of an expanding “flat” geometry, since the surface of the classroom is flat like a tabletop: if you start moving in one direction, you would never get back to your starting point.

Now play the movie backward for both examples. The balloon shrinks, the classroom shrinks. At some moment in the past, all the coins and desks would be on top of one another, a big bundle of stuff. That is the point of maximum compression that, extrapolated to its ultimate mathematical limit, would be a point of infinite mass-energy density. But of course, we cannot squeeze everything into a zero-volume point. This is a mathematical extrapolation, not physical reality. We still don’t know what happens as we get really close to this situation.

Alexander Friedmann: a meteorologist-turned-cosmologist

This image of an expanding geometry came from a remarkable paper published in June 1922 by Russian meteorologist-turned-cosmologist, Alexander Friedmann. In 1917, Einstein found the first solution for the geometry of the Universe, using his brand new theory of general relativity, the theory that attributes gravity to the curvature of space around a massive body. Einstein’s result was quickly followed by another solution by the Dutch Willem de Sitter, also from 1917.

Einstein’s solution pictured a static spherical universe with radius R and a “cosmological constant,” a parameter he put in by hand to find a static solution. How remarkable is it that with paper and pen in hand a human could devise a theory for the Universe as a whole? De Sitter’s solution was different. His universe was empty — that is, it had no matter, only the cosmological constant. It was later shown (by Cornelius Lanczos in 1923) that de Sitter’s solution was equivalent to a Universe filled with the cosmological constant expanding exponentially fast. This was of interest because observations were showing that the light from distant “nebulae” (later shown to be galaxies) was redshifted — that is, stretched toward the red end of the color spectrum (which goes from violet to red, like the rainbow). De Sitter and others suggested that this redshift was possibly due to the moving of the nebulae away from us, like the Doppler shift from car horns that change as they move away (lower pitch) or approach (higher pitch).

The Friedmann equations

Friedmann takes the problem from here, and in his paper dated June 29, 1922, discovers that one doesn’t need either to impose a static Universe (Einstein) or an empty one (de Sitter) to find solutions with expanding geometry. So, he takes the radius R to change in time, and solves for R(t), with the time variable denoting “the time that passed since Creation” (in Friedmann’s words). Friedmann discovered different solutions that depend on the relative value of the cosmological constant and other parameters. In the “Monotone World of the First Kind,” the Universe starts at a singularity at t =0 and expands in a rate that first decelerates and then accelerates in time forever. In the “Monotone World of the Second Kind,” expansion starts from a finite radius and goes on exponentially fast forever. Finally, Friedmann found what he called the “Periodic World,” where the Universe starts from a singularity at t = 0 and expands and contracts periodically in time.

In 1923, Friedmann published his book World as Space and Time, where he waxed philosophical about his discovery and how it will be decided by reliable data, which it was. More remarkably, he makes a connection between his periodic Universe and Hindu mythology, while making an estimate for the age of the Universe expanding from “nothingness”:

A non-static Universe represents a variety of cases. For example, it is possible that the radius of curvature constantly increases from a certain initial value; it is also possible that the radius changes periodically. In the latter case the Universe compresses into a point (into nothingness), then increases its radius to a certain value, and then again compresses into a point. Here one may recall the teaching of Indian philosophy about “periods of life.” It also provides an opportunity to speak about the world “created from nothingness.” But all these scenarios must be considered as curiosities which cannot be presently supported by solid astronomical experimental data. So far it is useless, due to the lack of reliable astronomical data, to cite any numbers that describe the life of our Universe. Yet if we compute, for the sake of curiosity, the time when the Universe was created from a point to its present state, i.e., time that has passed from the “creation of the world,” then we get at number equal to tens of billions of usual    years.

Friedmann passed away in 1925, never receiving in life the credit he deserved, and he has often been misquoted in the literature. But in his work and words, we see the achievements of a truly revolutionary thinker, looking forward to a time when data would confirm his vision for an expanding Universe.

In 1929, Edwin Hubble confirmed Vesto Slipher’s previous data on receding nebulae, since then correctly understood as galaxies in an expanding universe. We now call the cosmological constant — or something very similar to it — “dark energy.” The 2011 Nobel Prize in physics celebrates this discovery, crowning the work of the pioneers of modern cosmology. Now it is time to give Alexander Friedmann the credit he deserves.