632 – Fibonacci in Budapest
Put a pair of newborn rabbits, a buck and a doe, together in a pen. Assume it takes them a month to start reproducing, and another month for the female to give birth. Assume they produce another male and female pair to which the same applies. Assume no rabbits die. How many rabbits in the pen after one year?
The man who solved that riddle also introduced Europe to the decimal system of Hindi-Arabic numbers (0 to 9) we use today, replacing the Roman numerals (I, II, III, IV, etc.) that are so impractical for doing calculations.
Living from 1170-1250, he was perhaps the greatest mathematician in the mediaeval West, also giving us the bar we use for fractions, and the V-shape used in square root notation. His first name was Leonardo, and he was often called Pisano (i.e. ‘from Pisa’), Bigollo and Bonacci. But we know him as Fibonacci.
And his imaginary rabbit pairs, mechanically reproducing month after month, increase like this: 1-1-2-3-5-8-13-21-34-55-89-144-233. So in the 13th month, one year after the first couple of rabbits is placed in the pen, it contains exactly 233 pairs of long-ears (or 466 individual rabbits. That’s a lot of bunny burgers).
What’s special about Fibonacci’s numerical sequence is not just that each number is the sum of the two preceding ones, but that it keeps popping up again and again in maths, art and nature.
Among many other things, the Fibonacci Sequence determines the number of flower petals, the arrangement of seed pods on a pine cone, and the shape of both snail’s shells and entire galaxies. This sequence, it turns out, is how the Universe likes to do its sums.
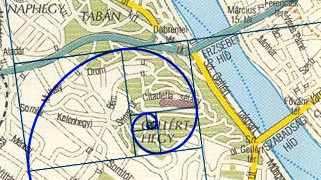
Graphically, the Fibonacci Sequence can be laid out as a Golden Spiral, that is: a spiral the growth factor of which is the Golden Ratio, a.k.a. φ (the Greek letter phi). To get to the bottom of phi (roughly 1.62) would require a shedload of maths. To see the Fibonacci Sequence in action, Golden Spiral-style, let me point you instead to the nearest snail’s shell. Or to the nearest galaxy. Or, bizarrely, to a map of Budapest.
The Fibonacci Sequence frequently crops up in architectural design – from classical Greek temples to modern buildings – but it seems unlikely that it would emerge from something as chaotic and random as unsupervised urban growth. Yet there it is: the telltale curl of a Fibonacci Sequence, following the streets in the centre of the Hungarian capital.
What mysterious force has arranged the alleyways and avenues of Budapest into a Fibonacci Sequence? Was it a joke by the city planners? Is this intelligent design at work – the ghost of Pythagoras pacing across the Pannonnian Plain? Or are we simply seeing things that aren’t there?
Budapest’s Fibonacci Trail begins just south of the Citadella, on the flank of Gellért Hill on the Buda (western) bank of the river. It takes a twist or two before the mathematical curl finds an actual road to dance the Fibonacci Tango with.
It then joins with a series of streets and avenues that form a suitably curved boulevard around the city centre: Bocskai Way, 23 October Street and József Irinyi Street on the Buda side, then across the Danube on the Petőfi Bridge, continuing on the Pest side with a series of Boulevards named Ferenc (Francis), József (Joseph), Erzsébet (Elisabeth), Terek (Grand) and Szent Istvan (St. Stephen). The Margaret Bridge then takes Fibonacci back across to Buda, but not before touching the southern tip of Margaret Island, the popular recreational area.
So what does this sequence tell us? For starters, if you look at it close up, the Golden Spiral doesn’t quite follow the road layout. But zoom out a bit, and the correspondence is close. Did Hungarian architects imitate the universe’s building-block numbers on the Budapest blueprint – wittingly or unwittingly? Or are we trying to shoehorn a cartographic perception into a map where it isn’t even present?
As one commenter on Rabbit – I mean, Reddit – said: “I believe Budapest can teach us something about mathematics or maybe not”. Hear, hear. So the mystery remains unsolved. Which is how we like ’em best.
Map found here on Reddit. Many thanks to Pal Szabo for alerting me to it. Drawing of the Golden Spiral taken here on LiveScience.







