We All Learned Physics’ Biggest Myth: That Projectiles Make A Parabola

It’s an incredibly useful approximation. But the truth takes us far deeper.
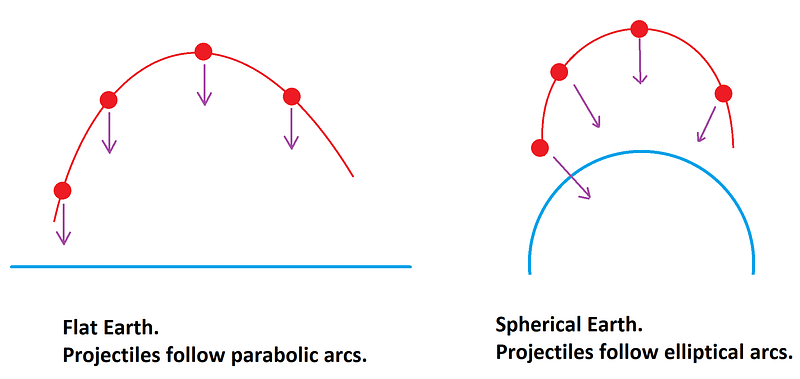
Anyone who’s ever taken a physics course has learned the same myth for centuries now: that any object thrown, shot, or fired in the gravitational field of Earth will trace out a parabola before striking the ground. If you neglect external forces like wind, air resistance, or any other terrestrial objects, this parabolic shape describes how the center-of-mass of your object moves extremely accurately, no matter what it is or what else is at play.
But under the laws of gravity, a parabola is an impossible shape for an object that’s gravitationally bound to the Earth. The math simply doesn’t work out. If we could design a precise enough experiment, we’d measure that projectiles on Earth make tiny deviations from the predicted parabolic path we all derived in class: microscopic on the scale of a human, but still significant. Instead, objects thrown on Earth trace out an elliptical orbit similar to the Moon. Here’s the unexpected reason why.
If you wanted to model the gravitational field at Earth’s surface, there are two simplifying assumptions you could make:
- the Earth, at least in your vicinity, is flat rather than curved,
- and that Earth’s gravitational field points straight down relative to your current location.
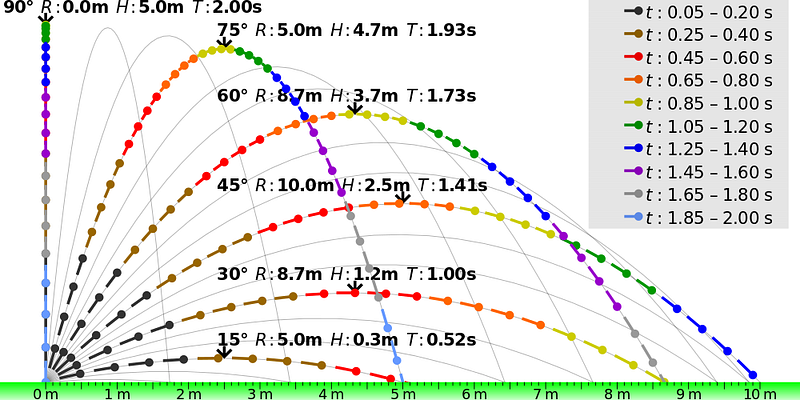
Any time you throw and release an object, therefore, it enters a situation known as free-fall. In the directions that are parallel to the Earth’s surface (horizontal), the speed of any projectile will remain constant. In the directions that are perpendicular to Earth’s surface (vertical), however, your projectile will accelerate downwards at 9.8 m/s²: the acceleration due to gravity at Earth’s surface. If you make these assumptions, then the trajectory you calculate will always be a parabola, exactly what we’re taught in physics classes around the globe.
But neither one of these assumptions are true. The Earth may appear flat — so indistinguishable from flat that we cannot detect it over the distances most projectiles cover — but the reality is that it has a spheroidal shape. Even over distances of just a few meters, the difference between a perfectly flat Earth and a curved Earth comes into play at the 1-part-in-1,000,000 level.
This approximation doesn’t matter so much for the trajectory of an individual projectile, but the second approximation does. From any location along its path, a projectile isn’t truly accelerated “straight down” in the vertical direction, but towards the center of the Earth. Over the same distance of a few meters, the difference in angle between “straight down” and “towards the center of the Earth” also comes into play at the 1-part-in-1,000,000 level, but this one makes a difference.
For a typical system, like a kicked soccer ball, a thrown football, or even a home run in baseball, the deviations from a parabola will show up at the level of tens to perhaps a hundred microns: smaller than a single paramecium. But the true trajectory is fascinating, and something derived by Johannes Kepler more than half a century before Newton came along.
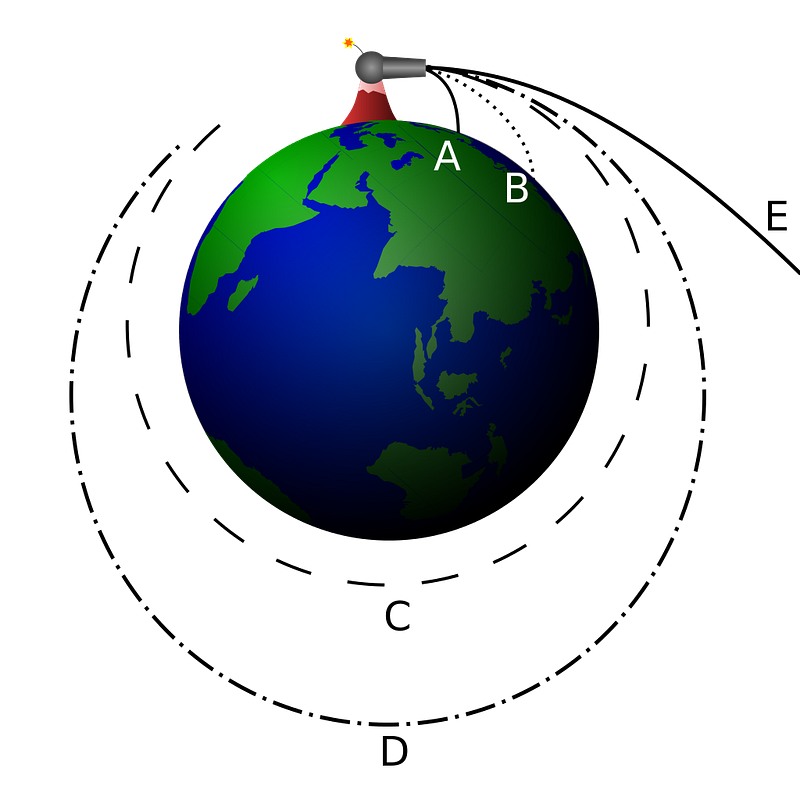
Just like the Moon, any projectile traces out an elliptical orbit, with the center of the Earth as one focus of that ellipse. The only difficulty for a projectile on Earth, as opposed to the Moon, is that the Earth itself gets in the way. As a result, we only see one tiny portion of the ellipse: the part that rises slightly above the Earth’s surface, reaches the peak of its trajectory (known as aphelion in celestial mechanics), and then falls back towards the Earth’s center.
As soon as the surface of the Earth gets in the way, however, the problem resets once again. If the projectile bounces at all, it will create an entirely new fragment-of-an-ellipse for its trajectory to follow, which can again be approximated very well by a parabola.
This happens for a simple reason that we typically take for granted: the Earth is made out of the same type of stuff, normal matter, that a typical projectile is made out of. Normal matter, which typically consists of protons, neutrons, and electrons, don’t just experience the gravitational force, but nuclear and electromagnetic forces as well. It’s the electromagnetic force that causes the typical interactions we experience between particles, enabling elastic and inelastic collisions, and preventing our projectiles from simply slipping through the Earth.
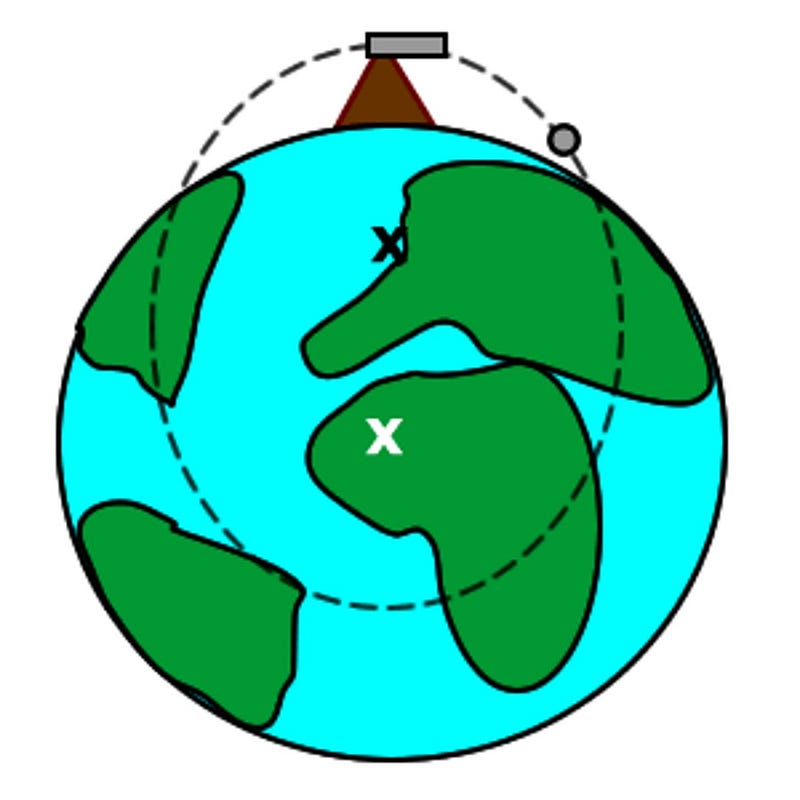
We can get around this problem, however, by imagining that we had something that didn’t interact with normal matter as our projectile. Perhaps it could be a low-energy neutrino; perhaps it could be a clump of dark matter. In either case, this projectile, once we released it, would only experience the gravitational force, and would pass through the surface and interior of the Earth itself under only the force of gravity.
If you expected that this particle would make a closed ellipse, however, and would return to its original location some ~90 minutes later back above the surface of the Earth from where it was first thrown, you’ve gone and made another approximation that isn’t quite right. When we calculate orbital trajectories, we treat the Earth as a single point: where all of its mass is located directly at its center. When we calculate trajectories of satellites, space stations, and even the Moon, this works just fine. But for a particle that passes through Earth’s surface, that approximation is no good any longer.
As long as you’re outside of a mass that’s shaped like a sphere (or spheroid), all of that mass gravitationally attracts you towards the center of the object. But if you’re only outside part of that mass (and only part of it is closer to the center of the world than you are), then all the parts of that mass that are outside of your present location cancel out.
You can only feel the gravitational effect of the mass that lies interior to you, assuming that everything external to your position is spherically symmetric. In electromagnetism, this is a consequence of Gauss’s Law; in gravitational physics, it’s a consequence of (the related) Birkhoff’s theorem. But what this practically means is that once you start falling through the Earth, you experience less and less of the internal mass’s gravitational pull.

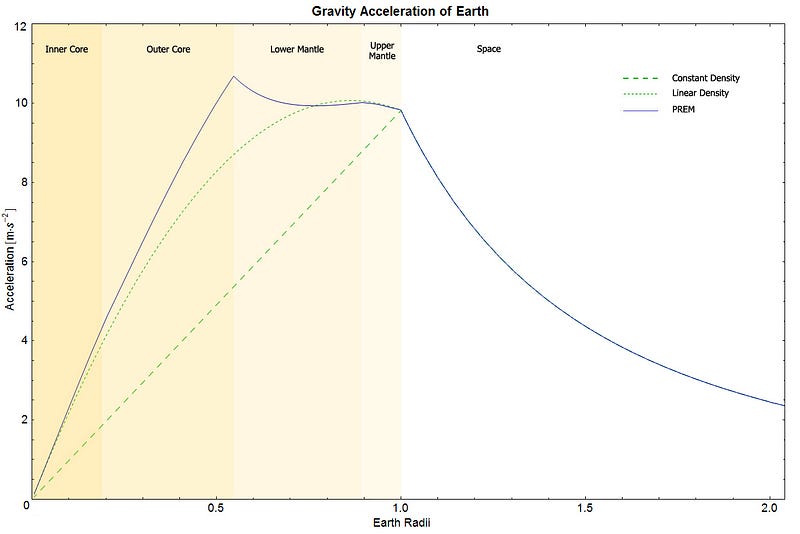
Rather than an ellipse, therefore, your trajectory would slowly change into a more oval, egg-like shape. As you passed through the less-dense crust and mantle and headed towards the inner and outer cores, you’d notice that there were not only smooth changes, but a few discontinuous “kinks” in the shape you traced out, corresponding to the various layers (of varying densities) in the Earth’s interior.
You would never re-emerge out of the other side of the Earth, but would fall through past the center by some amount, turning around in the core or the mantle depending on some subtle effects that aren’t so easy to calculate. Not only are the varying densities at different depths not completely known, but the rotational speeds of the varying layers interior to Earth have some uncertainties in them. If you consider even a single mass passing through the Earth, depending on the exact path it takes, dynamical friction begins to play a role as well.

When a particle passes by other massive particles, it gravitationally attracts them. If a particle speeds past all of the other ones, it will deflect their trajectories towards where it just passed through, which has the net effect of slowing the motion of the original particle. Depending on which way the original projectile was oriented with respect to Earth’s rotation and internal motions, this can affect the trajectory of whatever particle passes through the Earth.
Over the timespan of a single orbit, which still takes approximately 85–90 minutes or so, this can have a large enough effect so that the projectile doesn’t return to its original starting point. If we combine the effects of:
- the gravitation of an elliptical orbit due to a point mass,
- Birkhoff’s theorem for masses distributed throughout space,
- the varying density, composition, and (possibly) rotation rates of the Earth’s layers,
- and fold in the effects of dynamical friction,
a projectile won’t make a closed ellipse, but will instead return to a point offset by its starting point by up to as much as ~10 meters.
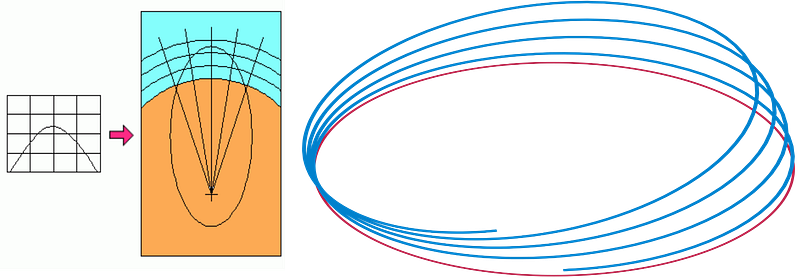
For most practical applications, it doesn’t hurt anyone to treat projectiles as having a parabolic trajectory. But if you care about micron-or-better precision, or are dealing with a large structure (like a suspension bridge) that spans 100 meters or more, you cannot treat the Earth’s gravitational field as a constant. Everything is accelerated not “downwards,” but towards the center of the Earth, enabling a projectile’s true trajectory — an ellipse — to be revealed.
Studying the various effects that are at play, both external to the Earth as well as within our planet’s interior, can also teach us when and under what circumstances it’s important to make these considerations. For most applications, air resistance is a far larger concern than any effects like the various layers of Earth’s interior or dynamical friction, and treating Earth’s gravitational field as a constant is totally justified. But for some problem, these differences matter. We are free to make whatever approximations we choose, but when our accuracy suffers beyond a critical threshold, we’ll have no one but ourselves to blame.

Ethan Siegel is the author of Beyond the Galaxy and Treknology. You can pre-order his third book, currently in development: the Encyclopaedia Cosmologica.