Everything you need to know about the math of Powerball

Playing the lottery is the ultimate low-risk, high-reward scenario. If you lose, you’re only out a few dollars: the cost of your bet. But if you win, even though the odds are stacked against you, the payoff is potentially life-changing, promising a lifetime of easy, luxurious living. You could not only realize all of your dreams that are reliant on financial fortunes, but those of your friends and relatives as well. And here in November of 2022, the Powerball jackpot has hit a whopping new record of $2.04 billion, a new record not just in terms of Powerball, but among all lottery games worldwide.

In order to win, you need to match five normal lottery numbers — white balls numbered 1-through-69 — plus the Powerball: a red ball numbered 1-through-26. Each Powerball ticket costs $2, plus you have the option to pay an extra $1 to activate the power play, a multiplier that increases your payout for non-jackpot prizes.

With a jackpot of $2.04 billion, plus an array of smaller prizes for matching some (but not all) of the balls drawn, here’s everything you need to know about what math says about playing the Powerball lottery.

Having just reached a record $1.9 billion, the Powerball Jackpot of November 7, 2022 has just broken the record for richest lottery jackpot in history. A single winner, excluding taxes, would fall into the top 2000 worldwide in terms of richest people alive today.

In particular there are some questions you should ask if you’re interested in the math behind Powerball:

• What are your odds of achieving each individual winning combination?
• How much does each winning possibility pay out?
• Is it worth it to activate the power play option?
• And finally, how big does the jackpot have to be in order for playing the Powerball lottery to be “worth it” from a mathematical point-of-view?

The idea of “worth it” is a subjective one to most people, but from a scientific/mathematical standpoint, it has a very particular meaning. It means that the amount you can expect to win, given an average outcome for the ticket, is greater than the amount you have to bet in order to play. If a Powerball lottery ticket costs $2, for example, buying a ticket would be above the “worth it” line if:

• You had a 51% chance of winning $4.
• Or, you had a 0.1% chance of winning $2001.
• Or, you had a 1-in-499,999 chance of winning $1,000,000.

But buying a ticket would fall below the “worth it” line if:

• You had only a 49% chance of winning $4.
• Or, you had a 0.1% chance of winning $1,999.
• Or, you had a 1-in-500,001 chance of winning $1,000,000.

This photo, taken at the Money Museum in Chicago, shows what $1,000,000 in cash, in twenty dollar bills, looks like. This is the ‘second prize’ in the Powerball jackpot, with roughly 1-in-11 million odds of such an outcome in Powerball.

Notice how small these differences are, but how in the earlier cases, you can expect to win more than you bet, while in the latter cases, you expect to bet more than you win. This is only an average, of course, but it comes out that way because:

• A 51% chance of winning $4 means that an average ticket is worth $2.02.
• A 0.1% chance of winning $2001 means that an average ticket is worth $2.001.
• And a 1-in-499,999 chance of winning $1,000,000 means that an average ticket is worth $2.000004.

On the other hand, for the latter examples — the ones that fall below the “worth it” line — the translation from probability to ticket worth works out as follows:

• A 49% chance of winning $4 means that an average ticket is worth $1.98.
• A 0.1% chance of winning $1999 means that an average ticket is worth $1.999.
• And a 1-in-500,001 chance of winning $1,000,000 means that an average ticket is worth $1.999996.

Mathematicians call this ratio of how-much-you-win vs. how-much-you-bet the expected value (or expectation value) of a problem. If your expected value is greater than 1.0, or more than the cost of a ticket, then it’s worth it to play. (And if not, then it isn’t!)

This diagram shows the likelihood of achieving outcomes within one, two, and three standard deviations of the mean value, assuming a Gaussian random distribution (i.e., Bell curve) of possible outcomes. Less likely outcomes, at the tail end(s) of this distribution, are often where the most interesting events occur. To get your expected value, you must multiply the odds of each possible outcome by the ‘reward’ for achieving each outcome.

That’s the general idea for any sort of gambling/gaming event: work out the balance between your odds of winning a prize (or all of the possible prizes) multiplied by how much that prize is actually worth, and then compare that to the actual cost of the “chance” you buy, to determine how much value each lottery ticket actually holds.

Specifically, then, what does this mean for the game of Powerball?

Let’s work it out.

In every game of Powerball, you get one ticket with five white numbers (out of 69 possible choices) and one red number (the Powerball, out of 26). In order to work out what the expected value is for each Powerball ticket, the first thing we have to do is understand what the set of possible outcomes are, and what your odds are of achieving each one. Here’s an infographic I made that breaks down what your odds are, on each ticket — remember, with five white numbers between 1-and-69 and one red number between 1-and-26 — of achieving each possible outcome.

The odds of achieving every possible outcome with a Powerball ticket as each and every relevant number is drawn. Note that the most likely outcome, of matching no numbers at all, is 65.23% likely, and that a total of 95.98% of the time, no prizes are awarded.

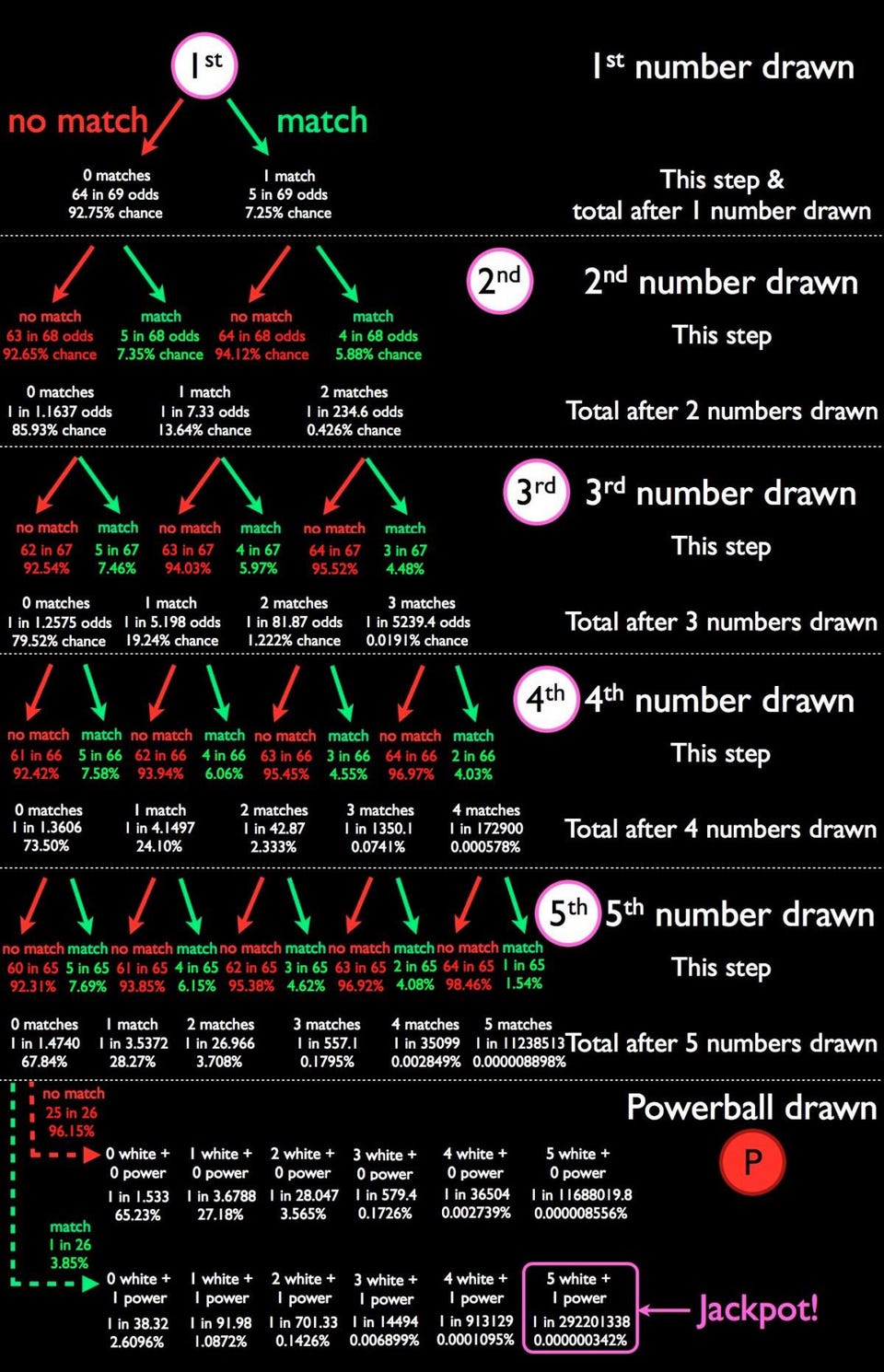
Your odds of actually winning the Powerball jackpot are pretty slim: one in 292,201,338. In fact, your odds of winning anything aren’t very good either, since the three most common results are:

• no matches of any type (65.23%),
• one white ball and no Powerball (27.18%), and
• two white balls and no Powerball (3.565%).

Those three options all pay out absolutely nothing, and add up to 95.98% of the possible results. In other words, without hitting the Powerball, you need at least three white balls to win anything at all.

That leaves the remaining 4.02% of the time as the only chances you have to actually win something. If the prizes that winning pays out — on average — crosses over a large enough threshold, it will be worth it to bet, and worth it to buy a ticket and play the game.

The possible options, which make up 4.02% of all Powerball tickets sold, for what you should match to win that prize, what the prize for winning is, and what your odds of achieving that specific outcome are.

These prizes vary tremendously in both your odds of achieving them and also in how much they pay out, assuming you do win them. According to the official Powerball site:

• Getting the Powerball with either 0 or 1 match from the white balls earns you $4.
• Hitting either the Powerball with 2 matching white balls or missing the Powerball but hitting 3 matching white balls earns you $7.
• Hitting either the Powerball with 3 matching white balls or missing the Powerball but hitting 4 matching white balls earns you $100.
• Hitting the Powerball with 4 matching white balls earns you $50,000.
• Missing the Powerball but hitting all 5 matching white balls earns you $1,000,000.
• And, of course, hitting all the numbers — the Powerball and all 5 white balls — earns you the Grand Prize.

If you want to calculate your expected value of each Powerball ticket purchased, you need to multiply your odds of winning each prize by the payout of each possible prize, and then add them all together to find out the total worth of each ticket. Given that each Powerball ticket costs $2, with an additional $1 possible for selecting the “Power Play” option, and that the “Grand Prize” payout depends both on the total jackpot amount and how many co-winners there are.

That said, we’ll come back to both the Power Play option and the Grand Prize payout in a bit; first, let’s look at the more likely non-Jackpot options.

The possible combinations of outcomes, the odds of achieving that outcome, the payout, and the contribution of that payout to the expected value of a $2 Powerball ticket. Note that the larger, less-likely prizes only contribute pennies to the overall value of a ticket.

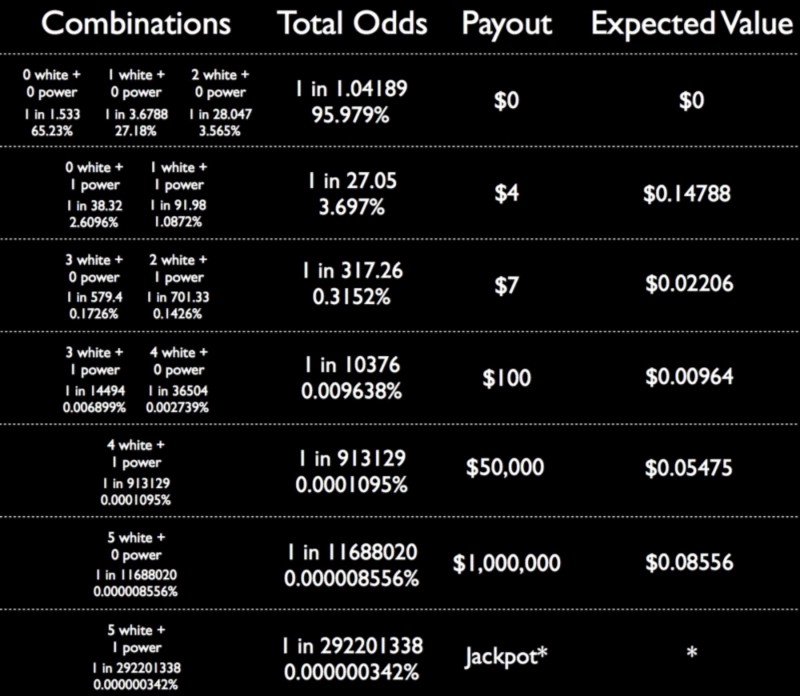
For every $2 ticket you buy, you can expect to recoup, on average:

• about $0.15 from the periodic $4 payouts,
• about $0.02 from the periodic $7 payouts,
• about $0.01 from the periodic $100 payouts,
• about $0.05 from the periodic $50,000 payouts,
• and about $0.09 from the periodic $1,000,000 payouts.

That means, all told, that the non-jackpot options make each ticket worth only about $0.32, which is a far cry from the $2 you invested. This teaches us two things:

1. It gives us the information we need to figure out how much the “Power Play” option is actually worth.
2. It let’s us know how much the Jackpot needs to pay out in order for buying a Powerball ticket to be “worth it,” mathematically.

First, let’s take on the Power Play option.

The odds of a Power Play along with the prize increases from using the Power Play option, with the odds given when the 10x multiplier both is and is not active.

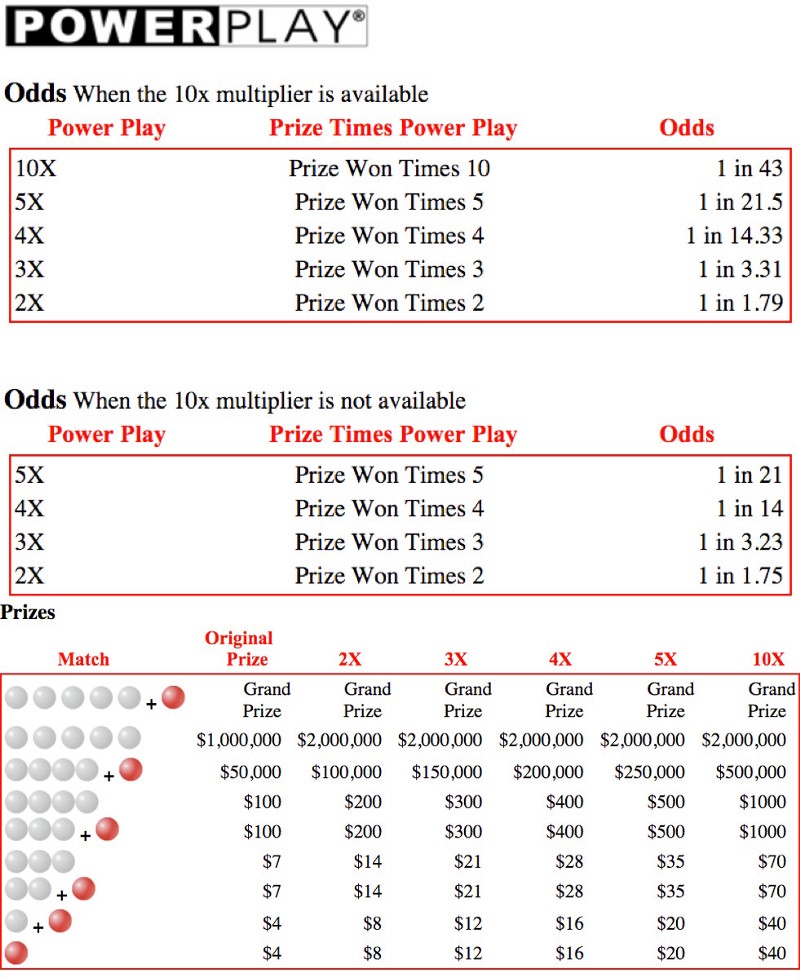
The Power Play option — which costs an extra $1.00, turning a $2 ticket into a $3 ticket — does the following:

• has no effect on the Jackpot/Grand Prize,
• always doubles the payout of the second-most-lucrative prize, and
• has a 1-in-1.75 chance of doubling (2x), a 1-in-3.23 chance of tripling (3x), a 1-in-14 chance of quadrupling (4x), or a 1-in-21 chance of quintupling (5x) the other prizes.
• If the 10x multiplier is active (only for Jackpots under $150 million), it reduces the chances of all the other options very slightly, and adds in a 1-in-43 chance of tenfold-multiplying (10x) all but the top two prizes.

So what’s the extra expected payoff for this additional $1 investment?

It transforms the expected worth of the non-jackpot options, per ticket, from being worth $0.32 up to being worth $0.81. This means you’re spending an extra $1.00 to increase your expected payout by $0.49, a lousy deal any way you slice it.

In fact, even if you happened to hit the 5x option, which happens only about 5% of the time, you only up your expected winnings to $1.34 for the non-jackpot options, which increases your winnings by a mere $1.02. That’s what you need to make it “worth” grabbing the Power Play option: a guaranteed 5x multiplier or better. The fact that the second-biggest-payout is only doubled, no matter what the Power Play multiplier happens to be, makes this a raw deal any way you slice it.

In other words, unless you know you’re guaranteed to get either the 5x or 10x multiplier, you should never take the Power Play option.

With a new record of a $1.9 billion Powerball Jackpot, a sole winner would become the largest-Jackpot lottery winner in history, immediately making them worth more (minus taxes, of course) than Christian Birkenstock, Michael Jordan, and Rihanna.

So finally, we come to the big prize: the Jackpot, or the Grand Prize, which you win by hitting all five numbers plus the Powerball, something that has a one-in-292,201,338 chance of happening. Given that your ticket costs $2, and the “rest of your ticket” is worth $0.32, it would make sense that as long as the expected value is $1.68 or higher from the Powerball Grand Prize, you’ll come out ahead, and should play.

And that’s correct, mathematically speaking! If your ticket costs $2, but is worth more than $2, it’s mathematically advantageous to play, and to purchase it.

But be careful, because this next step — from a mathematical point of view — is where they trick you. You might think, “Hey, so long as the Powerball Jackpot is more than $245 million, if my odds of winning are 1-in-292 million, I’ll come out ahead of the ‘$1.68 expected value’ per $2 ticket for winning the Jackpot.” But this is wrong for two reasons.

1. You have to pay taxes on your winnings, and the average Jackpot winner (dependent on your state’s specific tax laws) who takes the lump sum option only gets to keep about 37.2% of the Grand Prize’s value.
2. This also assumes that your winning ticket will be the only winning ticket, but the more people who play, the greater the odds that there will be multiple Grand Prize winners who have to split the prize.

At top, the Powerball ticket sales projections dependent on the size of the Jackpot; over half a billion tickets are expected for each Jackpot over $1 billion. At bottom, the expected value of a $2 Powerball ticket, which, when accounting for taxes and split Jackpots, peaks at Jackpot values of around half a billion dollars and decreases thereafter.

Taxes not only crush the expected payout from the Grand Prize, but also the second-largest prize as well: the $1,000,000 for hitting all five white numbers without the Powerball. The average payout for “winning $1,000,000” is only $590,000, which reduces your average ticket’s value by about $0.04 from what we just calculated before. But it’s the notion that “There will be one winner, and that winner will be me” that’s truly erroneous.

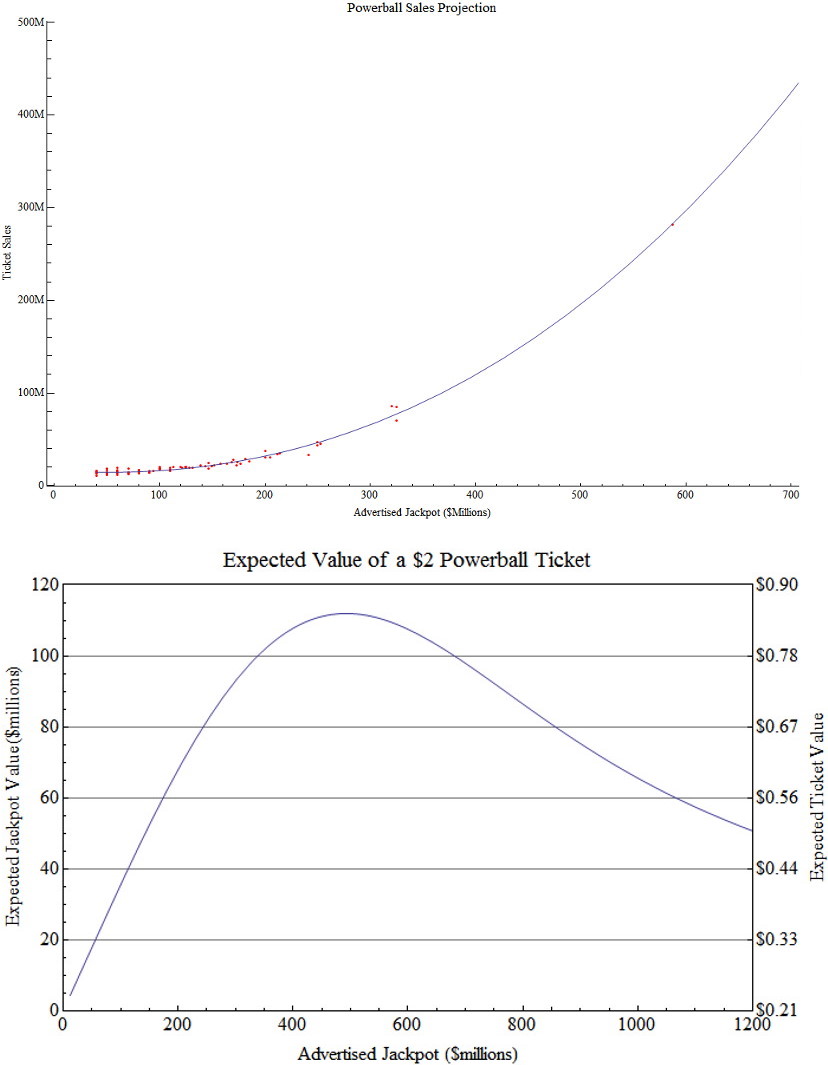
If 190 million tickets are sold — pretty typical for a near-$1B Jackpot — the odds are:

• 34% that no one wins the Jackpot,
• 37% that only one person wins the Jackpot,
• and 29% that two or more people win, and split, the Jackpot.

The greater the Jackpot, the greater the number of people who buy tickets. But once more than about 200 million tickets are sold, which happens at greater Jackpot levels, the less valuable each ticket becomes! A ticket sold for a $1,500 million (or $1.5 billion) Jackpot, in fact, would only be worth about half as much as a ticket sold for a $500 million Jackpot, because you’d most likely have to split the Jackpot, even if you won, with between three and seven other people.

All told, when you take both taxes and split Jackpots into account, you find that even at its maximum value, a $2 Powerball ticket is really only worth about $0.852, or just 43% of what you paid for it. If throwing $1.15 away is worth the amount of fun you’ll have, go right ahead. $0.85 of your ticket goes toward a “fair” lottery; the remaining $1.15 is simply your donation to whatever programs the Powerball lottery supports!