Even In A Quantum Universe, Space And Time Might Be Continuous, Not Discrete

When you hear ‘quantum,’ you probably think of splitting everything into discrete, indivisible chunks. That’s not necessarily right.
If you want to learn what the Universe is made out of at a fundamental level, your instinct would be to divide it up into smaller and smaller chunks until you can divide it no farther. Many of the things we observe, measure, or otherwise interact with in our macroscopic world are composed of smaller particles. If you sufficiently understand the most fundamental entities that underlie reality, as well as the laws that govern them, you should be able to understand and derive the rules and behaviors seen in the complex, larger world.
For matter and radiation as we understand it, there’s very good evidence that every single thing we’ve ever been able to observe or measure is quantum at some level. There are fundamental, indivisible, energy-carrying quanta that make up the matter and energy we know of. But quantized doesn’t necessarily mean discrete; you can be quantum and continuous as well. Which ones are space and time? Here’s how we’ll find out.

When we look to our description of the Universe — what it’s made of, what laws and rules govern it, what interactions occur or are even possible — there’s no one calculation you can perform to encompass all of it. There are the rules of the quantum Universe that govern the very, very small, describing the electromagnetic and nuclear (both weak and strong) forces as interactions between quantum particles and quantum fields.
If you have a system of matter or radiation that contains energy, if you examine it on a small enough scale, you’ll find that it can be broken down into individual quanta: energy packets which behave as either waves or particles, depending on what they interact with and how. Even though every system must be made up of individual quanta, with properties like mass, charge, spin and more, not every property of every quantum system is discrete.
Discrete means that you can divide something up into a localized, distinct sections that are inherently separate from one another. The counterpart of discrete is continuous, where there are no such division. If you take a conducting band of metal, for instance, you can ask questions about what energy level the electron occupies and where the electron is physically located. Surprisingly, the energy levels are discrete, but the position of the electron is not; it can be anywhere, continuously, within that band. Even if something is fundamentally quantum, not everything about it must be discrete.
Now, let’s try and fold gravity into the mix. Arguably the only important force in the Universe on the largest scales of all, gravity not have a self-consistent quantum description. We do not know whether a quantum theory of gravity even exists, although we conventionally assume it does and that we just have to find it.

Assuming that one exists, there’s a follow-up question we could ask that would illuminate an extraordinarily fundamental property of the Universe: are space and time discrete or continuous? Are there tiny, indivisible chunks of space that exist at some small scale that can be divided no further, where particles can only “jump” from one to the other? Is time broken up into uniformly sized chunks that pass by one discrete “instant” at a time?
Believe it or not, the idea that space or time could be quantized goes back not to Einstein, but to Heisenberg. Heisenberg’s famous uncertainty principle fundamentally limits how precisely certain pairs of quantities like position and momentum, energy and time, or angular momentum in two perpendicular directions can be precisely measured. If you tried to calculate certain physical quantities in quantum field theory, the expected value diverged, or went to infinity, which means they gave nonsense answers.
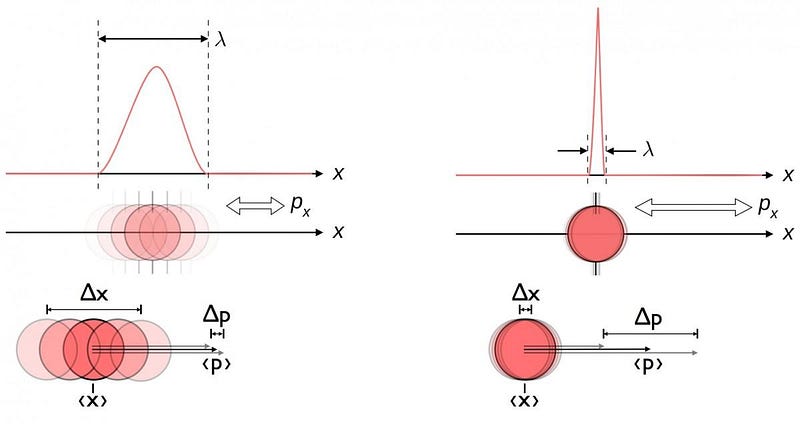
But upon noticing how those divergences occurred, he recognized that there was a potential fix: these unphysical infinities would disappear if you postulated that space wasn’t continuous, but rather had a minimum distance scale inherent to it. In the parlance of mathematics and physics, a theory without a minimum distance scale is non-renormalizable, which means you cannot make the probability of all the possible outcomes add up to one.
However, with a minimum distance scale, all those nonsense answers from earlier suddenly make sense: your quantum field theories are now fully renormalizable. We can calculate things sensibly, and get physically meaningful answers. To understand why, imagine taking a quantum particle that you understand and place it in a box. It will act like both a particle and a wave, but must always be confined to be inside the box.
Now, you decide to ask a critical question of this particle, “where is it?” The way you answer that is by making a measurement, which means causing another quantum of energy to interact with the one you placed in the box. You’ll get an answer, but that answer will also have an uncertainty inherent to it: proportional to ħ/L, where ħ is the Planck constant and L is the size of the box.
Under most circumstances, the box we’d deal with is large compared to the other distance scales we’re physically interested in, so even though ħ is small, the fraction ħ/L (if L is large) is even smaller. The uncertainty, therefore, is typically small compared to the measured answer you get.
But what if L is very small? What if L is so small that the uncertainty term, ħ/L, is larger than the answer term? In that case, the higher-order terms that we normally neglect, like (ħ/L)², (ħ/L)³ and so on, can no longer be ignored. The corrections get bigger and bigger, and there’s no sensible way to deconstruct the problem.
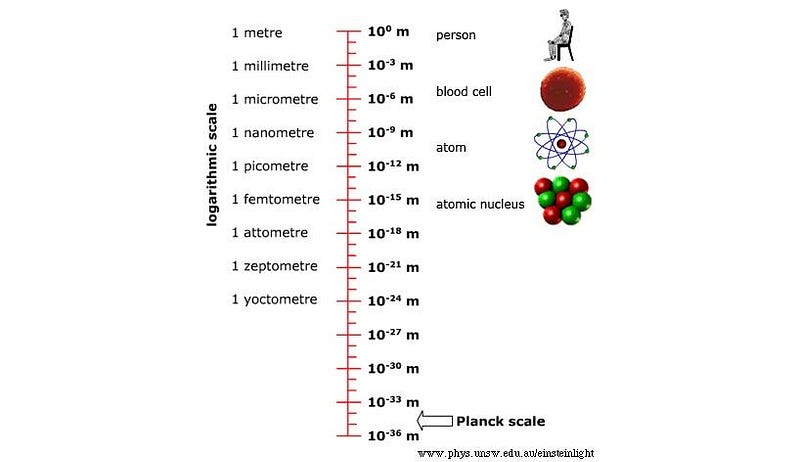
However, if you don’t treat space as continuous but rather as discrete, then there’s a lower limit to how small something can get: an effective limit to how small you’re allowed to make L, the size of your box. By introducing a cutoff scale, you restrict yourself from using an L that’s below a particular value. Imposing a minimum distance like this not only resolves the pathological case of a too-tiny box, but saves us a number of headaches that would otherwise plague us as we try to calculate how the quantum Universe behaves.
In the 1960s, physicist Alden Mean demonstrated that adding Einstein’s gravitation into the normal mix of quantum field theory only amplifies the uncertainty inherent to position; it therefore becomes impossible to make sense of distances shorter than a specific scale: the Planck distance. Below about 10^-35 meters, the physics calculations we can perform give answers that are nonsensical.
However, Einstein’s theory of gravity is a purely classical picture of gravitation, and as such there are a number of physical systems that it’s incapable of describing. For example, when an electron (a charged, massive, spinning quantum of energy) passes through a double slit, it will behave as though it’s simultaneously passing through both slits and once and interfering with itself. What happens to that electron’s gravitational field as it passes through that double slit?
Einstein’s theory cannot answer it. We assume that there’s a quantum theory of gravity out there, but we don’t know whether that theory will also require a distance-scale cutoff or not. Heisenberg’s original argument came about from trying (and failing) to renormalize Enrico Fermi’s original theory of beta decay; the development of electroweak theory and the Standard Model removed the need for a discrete minimum length. Perhaps, with a quantum theory of gravity, we won’t need a minimum length scale to renormalize any and all of our theories.
Right now, there are three possibilities for the fundamental nature of space and time, as we look to the future but with today’s understanding.
- Space and time are discrete. There is a shortest length scale, and it has a certain value. This possibility is exciting since it helps with renormalizing quantum field theories, but it poses big problems for relativity. Imagine you put down an imaginary ruler of the exact minimum allowable length. Now, your friend moves relative to the ruler while you remain stationary: you both measure different ruler lengths and hence, different fundamental length scales. Unless you’re willing to violate something important, like Lorentz invariance, this possibility creates big problems.
- Space and time are continuous. Perhaps every “problem” we associate with gravity today is simply an artifact of not having a complete theory of the quantum Universe. Perhaps space and time really are continuous entities: quantum in nature but incapable of being broken up into fundamental units. Just like the band structure of electrons in materials, perhaps the fabric of the Universe is fundamentally continuous, too.
- We’ll never know because there’s a fundamental, finite limit to our resolution. What’s real and fundamental don’t always equate to what a measuring device can reveal. If space is continuous but our ability to view or measure it is limited, it will always appear “blurred” below a certain distance scale. We wouldn’t be able to determine whether it was continuous or discrete, only that below a certain length scale, its structure cannot be resolved.

Remarkably, there may be a few different tests we can perform to determine whether gravity is a quantum force and whether space itself is discrete or continuous. Three years before he died, Jacob Bekenstein proposed passing a single photon through a crystal, which would impart momentum and cause the crystal to move by a slight amount. By continuously tuning the photon energy, you could then detect whether the “steps” the crystal moved by were discrete or continuous, and whether there was a threshold below which the crystal wouldn’t move at all.
Additionally, we’ve recently developed the ability to bring nanogram-scale objects into quantum superpositions of states, with the exact energy levels depending on the total gravitational self-energy. A sensitive enough experiment would be sensitive to whether gravity is quantized (or not), and when technology and experimental techniques make the requisite advances, we’ll at last be able to probe the regime of quantum gravity.
In General Relativity, matter and energy tell space how to curve, while curved space tells matter and energy how to move. But in General Relativity, space and time are continuous and non-quantized. All the other forces are known to be quantum in nature, and require a quantum description to match reality. We assume and suspect that gravitation is fundamentally quantum, too, but we aren’t sure. Furthermore, if gravity is ultimately quantum, we don’t know whether space and time remain continuous, or whether they become fundamentally discrete.
Quantum doesn’t necessarily mean that every property breaks down into an indivisible chunk. In conventional quantum field theory, spacetime is the stage upon which the various quanta act out the play of the Universe. At the core of it all should be a quantum theory of gravity. Until we can determine whether space and time are discrete, continuous, or unavoidably blurred, we cannot know our Universe’s nature at a fundamental level.
Ethan Siegel is the author of Beyond the Galaxy and Treknology. You can pre-order his third book, currently in development: the Encyclopaedia Cosmologica.