Ask Ethan: Why Do Gravitational Waves Travel Exactly At The Speed Of Light?

Travel the universe with Dr. Ethan Siegel as he answers the biggest questions of all

General Relativity has nothing to do with light or electromagnetism at all. So how to gravitational waves know to travel at the speed of light?

There are two fundamental classes of theories required to describe the entirety of the Universe. On the one hand, there’s quantum field theory, which describes electromagnetism and the nuclear forces, and accounts for all the particles in the Universe and the quantum interactions that govern them. On the other hand, there’s General Relativity, which explains the relationship between matter/energy and space/time, and describes what we experience as gravitation. Within the context of General Relativity, there’s a new type of radiation that arises: gravitational waves. Yet, despite having nothing to do with light, these gravitational waves must travel at the speed of light. Why is that? Roger Reynolds wants to know, asking:

We know that the speed of electromagnetic radiation can be derived from Maxwell’s equation[s] in a vacuum. What equations (similar to Maxwell’s — perhaps?) offer a mathematical proof that Gravity Waves must travel [at the] speed of light?

It’s a deep, deep question. Let’s dive into the details.

It’s possible to write down a variety of equations, like Maxwell’s equations, to describe some aspect of the Universe. We can write them down in a variety of ways, as they are shown in both differential form (left) and integral form (right). It’s only by comparing their predictions with physical observations can we draw any conclusion about their validity. (EHSAN KAMALINEJAD OF UNIVERSITY OF TORONTO)

It’s not apparent, at first glance, that Maxwell’s equations necessarily predict the existence of radiation that travels at the speed of light. What those equations ⁠ — which govern classical electromagnetism ⁠ — clearly tell us are about the behavior of:

stationary electric charges,
electric charges in motion (electric currents),
static (unchanging) electric and magnetic fields,
and how those fields and charges move, accelerate, and change in response to one another.

Now, using the laws of electromagnetism alone, we can set up a physically relevant system: that of a low-mass, negatively charged particle orbiting a high-mass, positively charged one. This was the original model of the Rutherford atom, and it came along with a big, existential crisis. As the negative charge moves through space, it experiences a changing electric field, and accelerates as a result. But when a charged particle accelerates, it has to radiate power away, and the only way to do so is through electromagnetic radiation: i.e., light.

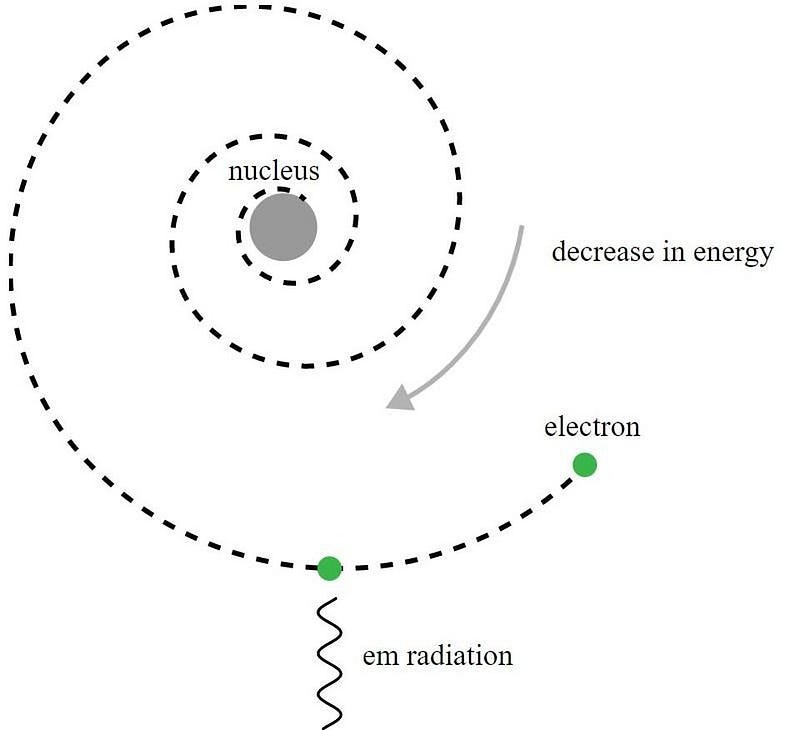
In the Rutherford model of the atom, electrons orbited the positively charged nucleus, but would emit electromagnetic radiation and see that orbit decay. It required the development of quantum mechanics, and the improvements of the Bohr model, to make sense of this apparent paradox. (JAMES HEDBERG / CCNY / CUNY)

This has two effects that are calculable within the framework of classical electrodynamics. The first effect is that the negative charge will spiral into the nucleus, as if you’re radiating power away, you have to get that energy from somewhere, and the only place to take it from is the kinetic energy of the particle in motion. If you lose that kinetic energy, you inevitably will spiral towards the central, attracting object.

The second effect that you can calculate is what’s going on with the emitted radiation. There are two constants of nature that show up in Maxwell’s equations:

ε_0, the permittivity of free space, which is the fundamental constant describing the electric force between two electric charges in a vacuum.
μ_0, the permeability of free space, which you can think of as the constant that defines the magnetic force produced by two parallel conducting wires in a vacuum with a constant current running through them.

When you calculate the properties of the electromagnetic radiation produced, it behaves as a wave whose propagation speed equals (ε_0 · μ_0)^(-1/2), which just happens to equal the speed of light.

Relativistic electrons and positrons can be accelerated to very high speeds, but will emit synchrotron radiation (blue) at high enough energies, preventing them from moving faster. This synchrotron radiation is the relativistic analog of the radiation predicted by Rutherford so many years ago, and has a gravitational analogy if you replace the electromagnetic fields and charges with gravitational ones.(CHUNG-LI DONG, JINGHUA GUO, YANG-YUAN CHEN, AND CHANG CHING-LIN, ‘SOFT-X-RAY SPECTROSCOPY PROBES NANOMATERIAL-BASED DEVICES’)

In electromagnetism, even if the details are quite the exercise to work out, the overall effect is straightforward. Moving electric charges that experience a changing external electromagnetic field will emit radiation, and that radiation both carries energy away and itself moves at a specific propagation speed: the speed of light. This is a classical effect, which can be derived with no references to quantum physics at all.

Now, General Relativity is also a classical theory of gravity, with no references to quantum effects at all. In fact, we can imagine a system very analogous to the one we set up in electromagnetism: a mass in motion, orbiting around another mass. The moving mass will experience a changing external gravitational field (i.e., it will experience a change in spatial curvature) which causes it to emit radiation that carries energy away. This is the conceptual origin of gravitational radiation, or gravitational waves.

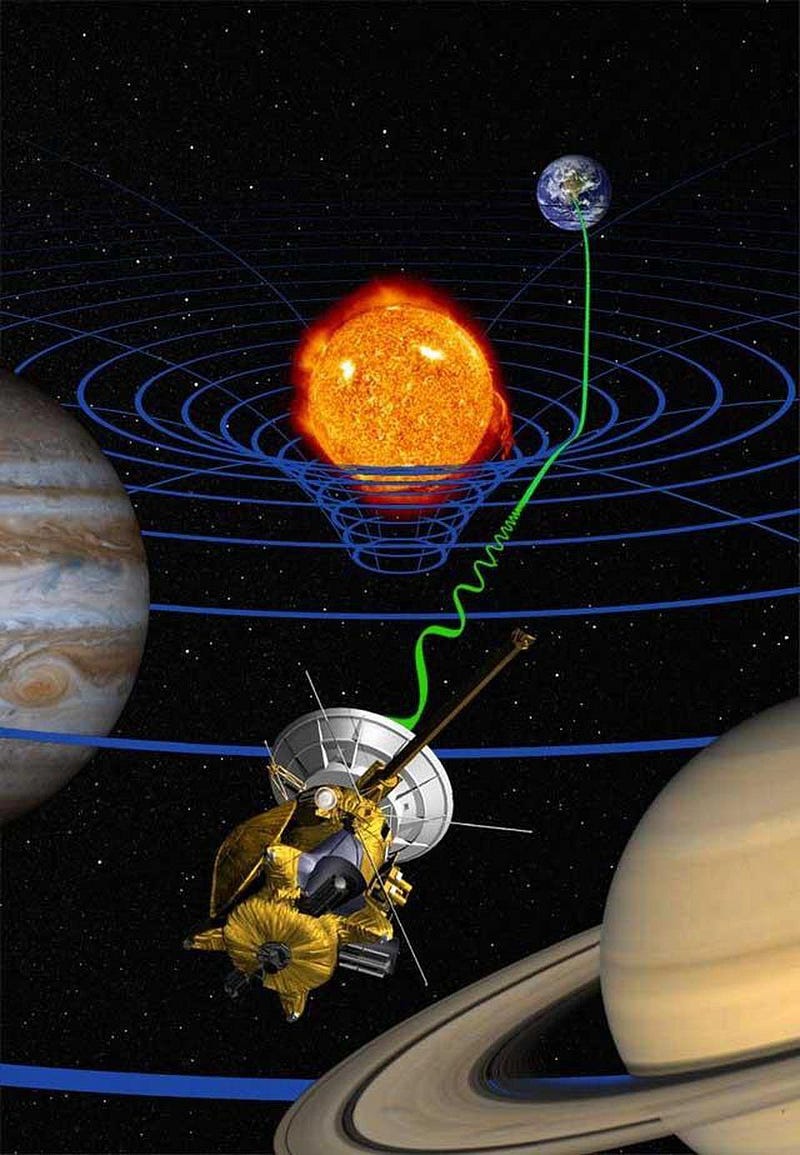
There is, perhaps, no better analogy for the radiation-reaction in electromagnetism than the planets orbiting the Sun in gravitational theories. The Sun is the largest source of mass, and curves space as a result. As a massive planet moves through this space, it accelerates, and by necessity that implies it must emit some type of radiation to conserve energy: gravitational waves. (NASA/JPL-CALTECH, FOR THE CASSINI MISSION)

But why ⁠ — as one would be inclined to ask ⁠ — do these gravitational waves have to travel at the speed of light? Why does the speed of gravity, which you might imagine could take on any value at all, have to exactly equal the speed of light? And, perhaps most importantly, how do we know?

Imagine what might happen if you were to suddenly pull the ultimate cosmic magic trick, and made the Sun simply disappear. If you did this, you wouldn’t see the skies go dark for 8 minutes and 20 seconds, which is the amount of time it takes light to travel the ~150 million km from the Sun to Earth. But gravitation doesn’t necessarily need to be the same way. It’s possible, as Newton’s theory predicted, that the gravitational force would be an instantaneous phenomenon, felt by all objects with mass in the Universe across the vast cosmic distances all at once.

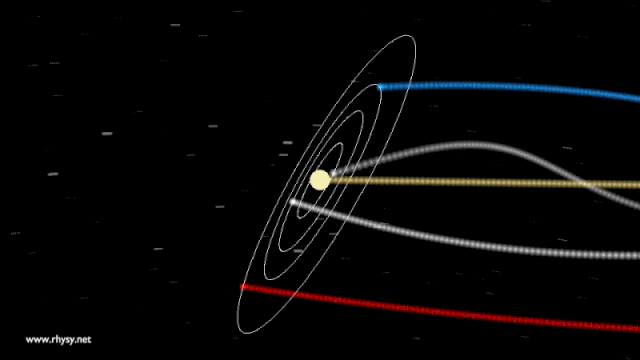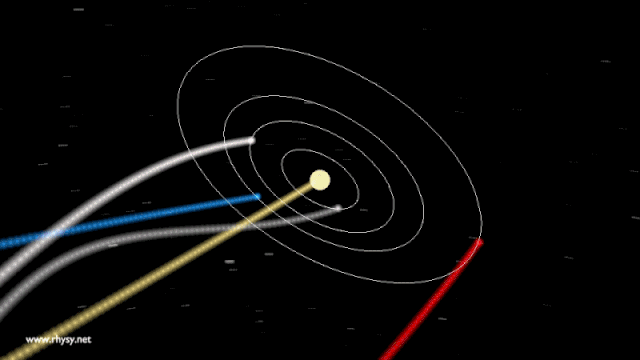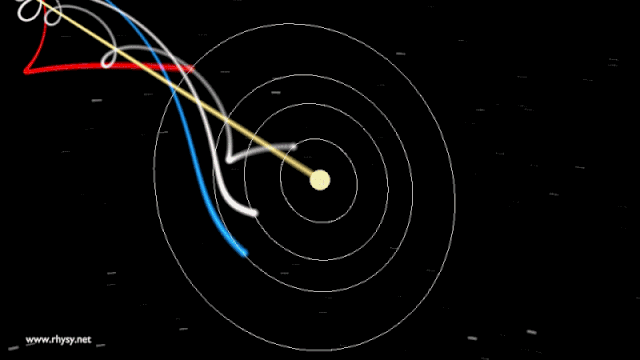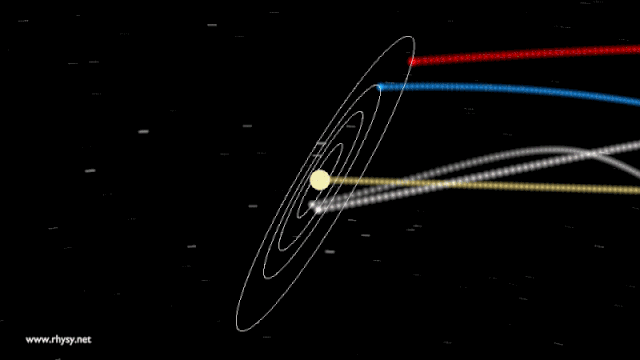
An accurate model of how the planets orbit the Sun, which then moves through the galaxy in a different direction-of-motion. If the Sun were to simply wink out of existence, Newton’s theory predicts that they would all instantaneously fly off in straight lines, while Einstein’s predicts that the inner planets would continue orbiting for shorter periods of time than the outer planets. (RHYS TAYLOR)

What would happen under this hypothetical scenario? If the Sun were to somehow disappear at one particular instant, would the Earth fly off in a straight line immediately? Or would the Earth continue to move in its elliptical orbit for another 8 minutes and 20 seconds, only deviating once that changing gravitational signal, propagating at the speed of light, reached our world?

If you ask General Relativity, the answer is much closer to the latter, because it isn’t mass that determines gravitation, but rather the curvature of space, which is determined by the sum of all the matter and energy in it. If you were to take the Sun away, space would go from being curved to being flat, but only in the location where the Sun physically was. The effect of that transition would then propagate radially outwards, sending very large ripples — i.e., gravitational waves — propagating through the Universe like ripples in a 3D pond.

Whether through a medium or in vacuum, every ripple that propagates has a propagation speed. In no cases is the propagation speed infinite, and in theory, the speed at which gravitational ripples propagate should be the same as the maximum speed in the Universe: the speed of light. (SERGIU BACIOIU/FLICKR)

In the context of relativity, whether that’s Special Relativity (in flat space) or General Relativity (in any generalized space), the speed of anything in motion is determined by the same things: its energy, momentum, and rest mass. Gravitational waves, like any form of radiation, have zero rest mass and yet have finite energies and momenta, meaning that they have no option: they must always move at the speed of light.

This has a few fascinating consequences.

Any observer in any inertial (non-accelerating) reference frame would see gravitational waves moving at exactly the speed of light.
Different observers would see gravitational waves redshifting and blueshifting due to all the effects — such as source/observer motion, gravitational redshift/blueshift, and the expansion of the Universe — that electromagnetic waves also experience.
The Earth, therefore, is not gravitationally attracted to where the Sun is right now, but rather where the Sun was 8 minutes and 20 seconds ago.

The simple fact that space and time are related by the speed of light means that all of these statements must be true.

Gravitational radiation gets emitted whenever a mass orbits another one, which means that over long enough timescales, orbits will decay. Before the first black hole ever evaporates, the Earth will spiral into whatever’s left of the Sun, assuming nothing else has ejected it previously. Earth is attracted to where the Sun was approximately 8 minutes ago, not to where it is today. (AMERICAN PHYSICAL SOCIETY)

This last statement, about the Earth being attracted to the Sun’s position from 8 minutes and 20 seconds ago, was a truly revolutionary difference between Newton’s theory of gravity and Einstein’s General Relativity. The reason it’s revolutionary is for this simple fact: if gravity simply attracted the planets to the Sun’s prior location at the speed of light, the planets’ predicted locations would mismatch severely with where they actually were observed to be.

It’s a stroke of brilliance to realize that Newton’s laws require an instantaneous speed of gravity to such precision that if that were the only constraint, the speed of gravity must have been more than 20 billion times faster than the speed of light! But in General Relativity, there’s another effect: the orbiting planet is in motion as it moves around the Sun. When a planet moves, you can think of it riding over a gravitational ripple, coming down in a different location from where it went up.

When a mass moves through a region of curved space, it will experience an acceleration owing to the curved space it inhabits. It also experiences an additional effect due to its velocity as it moves through a region where the spatial curvature is constantly changing. These two effects, when combined, result in a slight, tiny difference from the predictions of Newton’s gravity. (DAVID CHAMPION, MAX PLANCK INSTITUTE FOR RADIO ASTRONOMY)

In General Relativity, as opposed to Newton’s gravity, there are two big differences that are important. Sure, any two objects will exert a gravitational influence on the other, by either curving space or exerting a long-range force. But in General Relativity, these two extra pieces are at play: each object’s velocity affects how it experiences gravity, and so do the changes that occur in gravitational fields.

The finite speed of gravity causes a change in the gravitational field that departs significantly from Newton’s predictions, and so do the effects of velocity-dependent interactions. Amazingly, these two effects cancel almost exactly. It’s the tiny inexactness of this cancellation that allowed us to first test whether Newton’s “infinite speed” or Einstein’s “speed of gravity equals the speed of light” model matched the physics of our Universe.

To test out what the speed of gravity is, observationally, we’d want a system where the curvature of space is large, where gravitational fields are strong, and where there’s lots of acceleration taking place. Ideally, we’d choose a system with a large, massive object moving with a changing velocity through a changing gravitational field. In other words, we’d want a system with a close pair of orbiting, observable, high-mass objects in a tiny region of space.

Nature is cooperative with this, as binary neutron star and binary black hole systems both exist. In fact, any system with a neutron star has the ability to be measured extraordinarily precisely if one serendipitous thing occurs: if our perspective is exactly aligned with the radiation emitted from the pole of a neutron star. If the path of this radiation intersects us, we can observe a pulse every time the neutron star rotates.

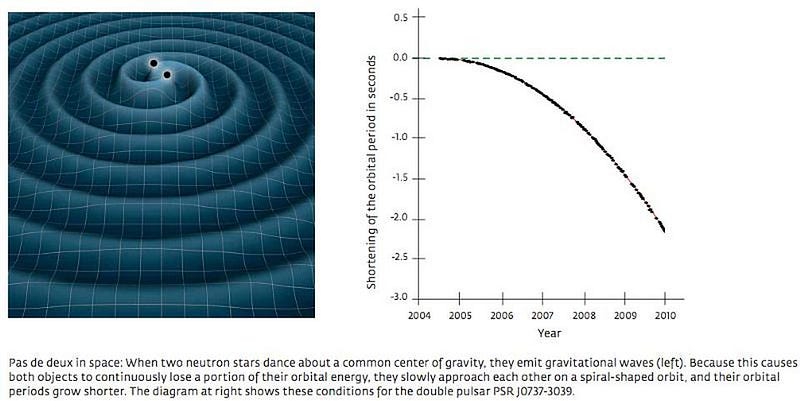
The rate of orbital decay of a binary pulsar is highly dependent on the speed of gravity and the orbital parameters of the binary system. We have used binary pulsar data to constrain the speed of gravity to be equal to the speed of light to a precision of 99.8%, and to infer the existence of gravitational waves decades before LIGO and Virgo detected them. However, the direct detection of gravitational waves was a vital part of the scientific process, and the existence of gravitational waves would still be in doubt without it. (NASA (L), MAX PLANCK INSTITUTE FOR RADIO ASTRONOMY / MICHAEL KRAMER (R))

As the neutron stars orbit, the pulsing one — known as a pulsar — carries extraordinary amounts of information about the masses and orbital periods of both components. If you observe this pulsar in a binary system for a long period of time, because it’s such a perfectly regular emitter of pulses, you should be able to detect whether the orbit is decaying or not. If it is, you can even extract a measurement for the emitted radiation: how quickly does it propagate?

The predictions from Einstein’s theory of gravity are incredibly sensitive to the speed of light, so much so that even from the very first binary pulsar system discovered in the 1980s, PSR 1913+16 (or the Hulse-Taylor binary), we have constrained the speed of gravity to be equal to the speed of light with a measurement error of only 0.2 %!

*The quasar QSO J0842+1835, whose path was gravitationally altered by Jupiter in 2002, allowing an indirect confirmation that the speed of gravity equals the speed of light.* (FOMALONT ET AL. (2000), APJS 131, 95–183)

That’s an indirect measurement, of course. We performed a second type of indirect measurement in 2002, when a chance coincidence lined up the Earth, Jupiter, and a very strong radio quasar (QSO J0842+1835) all along the same line-of-sight. As Jupiter moved between Earth and the quasar, the gravitational bending of Jupiter allowed us to indirectly measure the speed of gravity.

The results were definitive: they absolutely ruled out an infinite speed for the propagation of gravitational effects. Through these observations alone, scientists determined that the speed of gravity was between 2.55 × 10⁸ m/s and 3.81 × 10⁸ m/s, completely consistent with Einstein’s predictions of 299,792,458 m/s.

Artist’s illustration of two merging neutron stars. The rippling spacetime grid represents gravitational waves emitted from the collision, while the narrow beams are the jets of gamma rays that shoot out just seconds after the gravitational waves (detected as a gamma-ray burst by astronomers). The gravitational waves and the radiation must travel at the same speed to a precision of 15 significant digits. (NSF / LIGO / SONOMA STATE UNIVERSITY / A. SIMONNET)

But the greatest confirmation that the speed of gravity equals the speed of light comes from the 2017 observation of a kilonova: the inspiral and merger of two neutron stars. A spectacular example of multi-messenger astronomy, a gravitational wave signal arrived first, recorded in both the LIGO and Virgo detectors. Then, 1.7 seconds later, the first electromagnetic (light) signal arrived: the high-energy gamma rays from the explosive cataclysm.

Because this event took place some 130 million light-years away, and the gravitational and light signals arrived with less than a two second difference between them, we can constrain the possible departure of the speed of gravity from the speed of light. We now know, based on this, that they differ by less than 1 part in 10¹⁵, or less than one quadrillionth of the actual speed of light.

Illustration of a fast gamma-ray burst, long thought to occur from the merger of neutron stars. The gas-rich environment surrounding them could delay the arrival of the signal, explaining the observed 1.7 second difference between the arrivals of the gravitational and electromagnetic signatures. (ESO)

Of course, we think that these two speeds are exactly identical. The speed of gravity should equal the speed of light so long as both gravitational waves and photons have no rest mass associated with them. The 1.7 second delay is very likely explained by the fact that gravitational waves pass through matter unperturbed, while light interacts electromagnetically, potentially slowing it down as it passes through the medium of space by just the smallest amount.

The speed of gravity really does equal the speed of light, although we don’t derive it in the same fashion. Whereas Maxwell brought together electricity and magnetism — two phenomena that were previously independent and distinct — Einstein simply extended his theory of Special Relativity to apply to all spacetimes in general. While the theoretical motivation for the speed of gravity equaling the speed of light was there from the start, it’s only with observational confirmation that we could know for certain. Gravitational waves really do travel at the speed of light!

Submit your Ask Ethan questions to startswithabang at gmail dot com!

Ethan Siegel is the author of Beyond the Galaxy and Treknology. You can pre-order his third book, currently in development: the Encyclopaedia Cosmologica.

Travel the universe with Dr. Ethan Siegel as he answers the biggest questions of all