Ask Ethan: What Does It Mean That Quantum Gravity Has No Symmetry?

The quest for a quantum theory of gravity is the holy grail of physics. Here’s why it’s murkier than anyone expected.

If you want to fully describe how the Universe works at a fundamental level, you have to look at it in two different — and incompatible — ways. To describe the particles and their electromagnetic and nuclear interactions, you need to use the framework of quantum field theory (QFT), where quantum fields permeate the Universe and their excitations give rise to the particles we know of. To describe how every quantum of matter and energy moves through the Universe, we need the framework of General Relativity (GR), where matter and energy define how spacetime is curved, and curved spacetime tells matter and energy how to move.

Yet these two theories are mutually incompatible; to make them work together, we’d need to develop a working theory of quantum gravity. Yet a new paper, just published, has Alex Knapp puzzled, leading him to ask:

What does it mean that quantum gravity doesn’t have symmetry?

It’s a fascinating find with big implications. Let’s find out what it means.

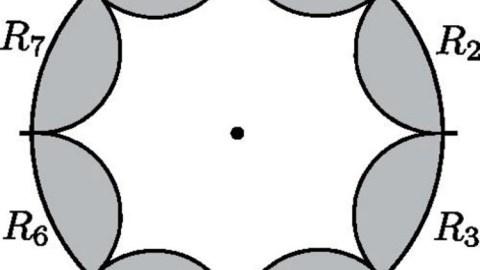
When you hear the word “symmetry,” there are probably all sorts of images that pop into your mind. Some letters of the alphabet — like “A” or “T” — display a symmetry where if you drew a vertical line down their centers, the left sides and the right sides are symmetric. Other letters — like “B” or “E” — have a similar symmetry but in a different direction: horizontally, where the tops and bottoms are symmetric. Still others — such as “O” — have rotational symmetry, where no matter how many degrees you rotate it, its appearance is unchanged.

These are some examples of symmetry that are easy to visualize, but they’re not exhaustive. Sure, some systems have no differences from their mirror reflections, known as a parity symmetry. Others demonstrate rotational symmetries, where it doesn’t matter what angle you view it from. But there are many others, all of vital importance.

Some systems are the same for matter as they are for antimatter: they exhibit charge conjugation symmetry. Some systems obey the same laws if you evolve them forwards in time as they do if you evolve them backwards in time: time-reversal symmetry. Still others don’t depend on your physical location (translational symmetry) or on when you’re viewing your system (time-translational symmetry) or on which non-accelerating reference frame you occupy (Lorentz symmetry).

Some physical systems have these symmetries; others don’t. Dropping a ball off of a cliff obeys time-reversal symmetry; cooking scrambled eggs does not. Flying through space with your engines turned off obeys Lorentz symmetry; accelerating, with your engines firing at full power, does not.

It isn’t just physical systems that can obey (or disobey) symmetries. Whenever you have an equation (or a quantitative theory in general), you can test them to see which symmetries they obey and which ones they don’t.

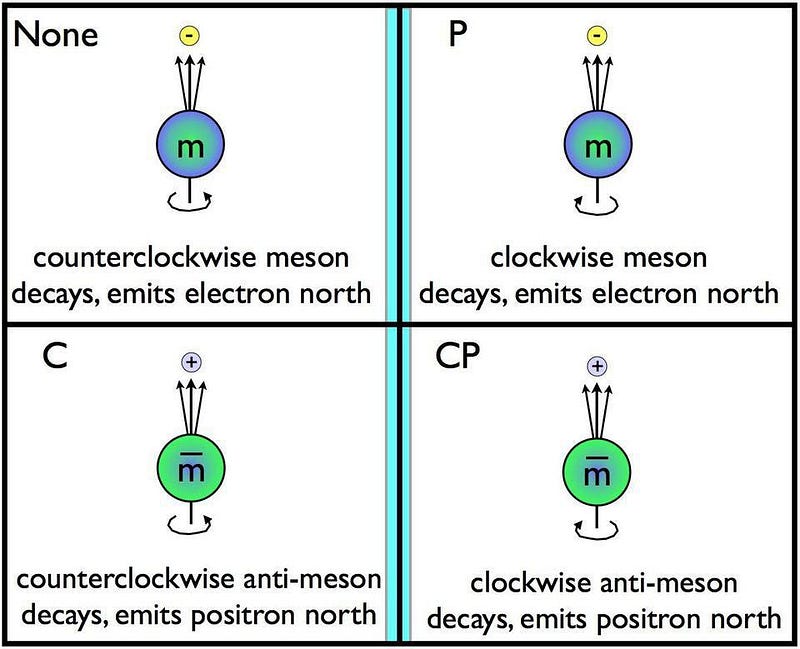
Within various QFTs, for example, particles experiencing the electromagnetic force obey parity, charge conjugation, and time-reversal symmetries all independently of one another. Electromagnetism is the same for particles regardless of their direction of motion; the same for particles and antiparticles; the same forwards in time as backwards in time.

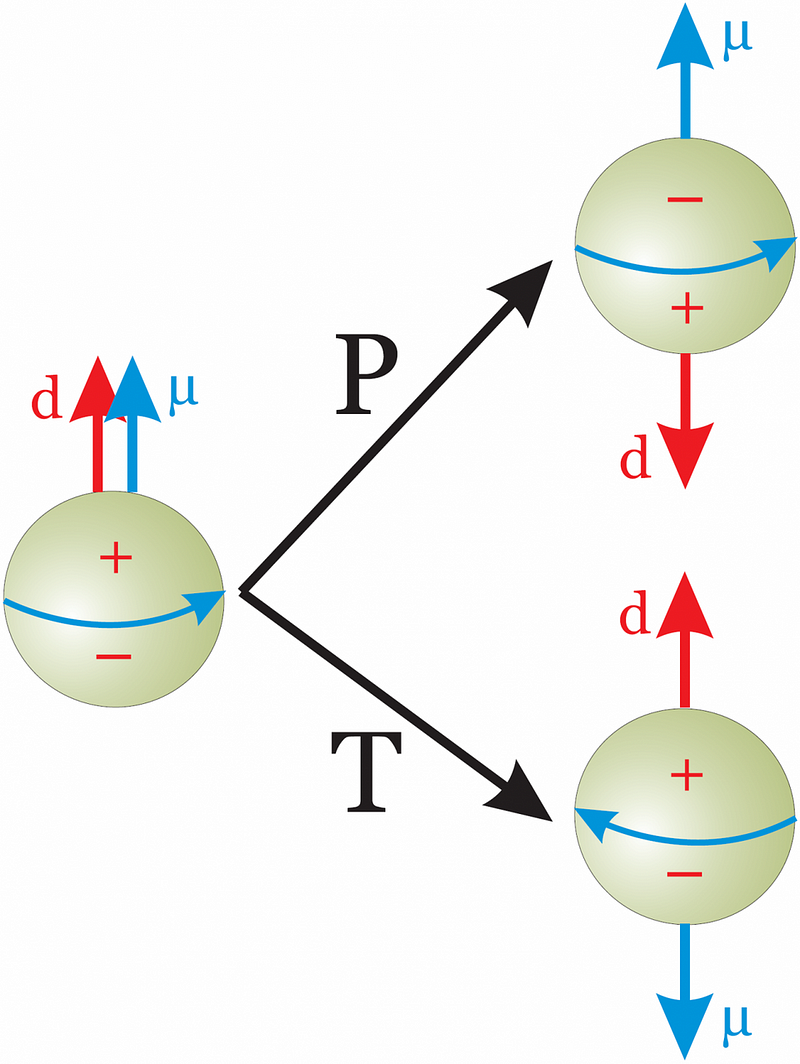
Particles experiencing the weak nuclear force, on the other hand, violate parity, charge conjugation, and time-reversal individually. Left-handed muons decay differently from right-handed muons. Neutral kaons and neutral anti-kaons have different properties. And the decays of B-mesons have time-asymmetric transformation rates. But even the weak interactions obey the combination of all three symmetries: if you perform an experiment on a particle in motion that moves forward in time and an antiparticle with its motion reflected moving backwards in time, you get the same physical results.

Within GR, various spacetimes obey different sets of symmetry. The (Schwarzschild) spacetime describing a non-rotating black hole exhibits time-translation, mirror, and full rotational symmetries. The (Kerr) spacetime describing a rotating black hole exhibits time-translation symmetry, but only has rotational symmetries about one axis.

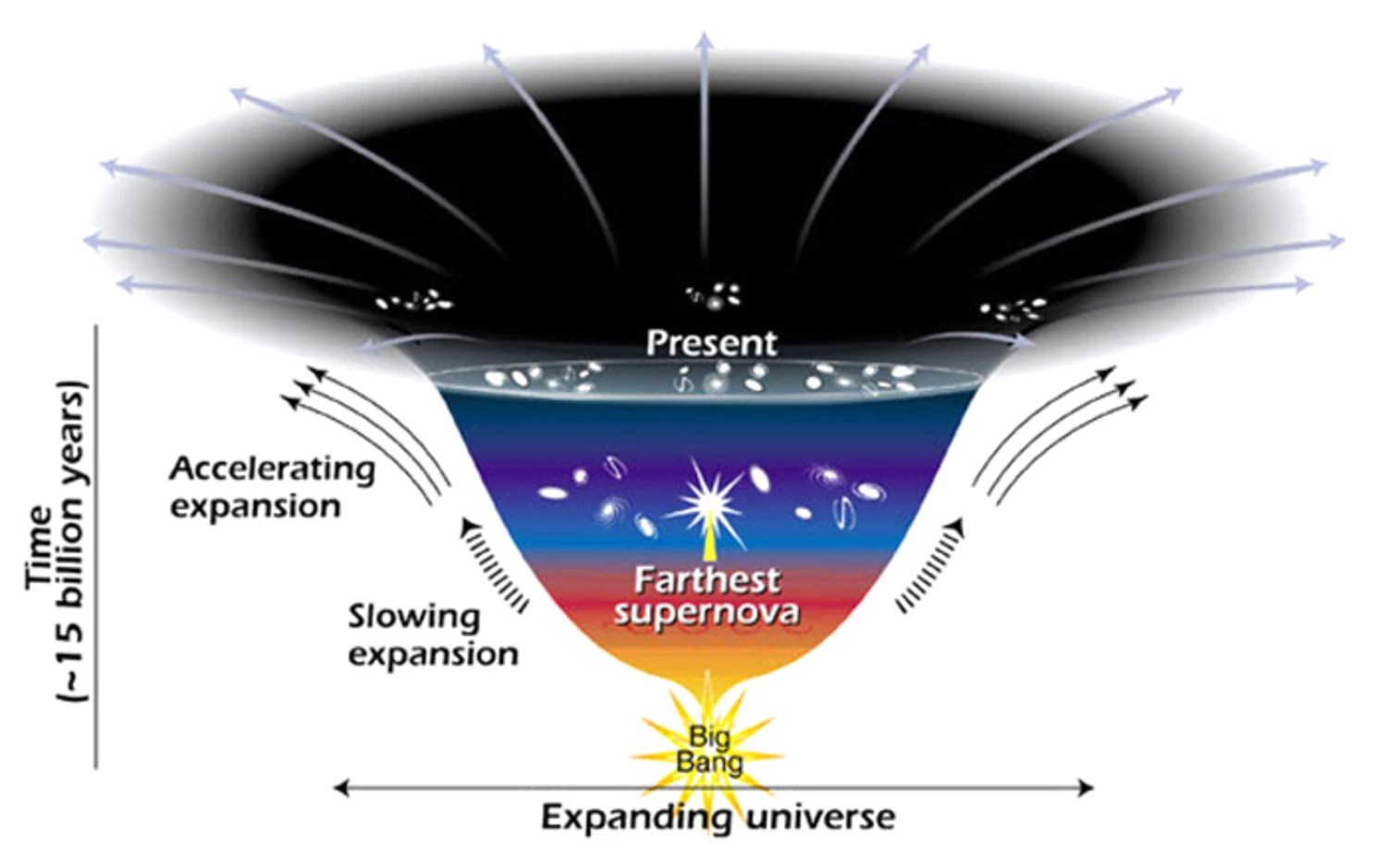
The (Friedmann-Lemaitre-Robertson-Walker) spacetime describing the expanding Universe, on the other hand, has a slew of symmetries it does obey, but time-translation isn’t one of them: an expanding Universe is different from one moment in time to the next.

In general, these symmetries are profoundly important to our understanding of the Universe, and have enormous additional implications for reality. You see, there’s a brilliant theorem at the intersection of physics and mathematics that states the following: every unique mathematical symmetry exhibited by a physical theory necessarily implies an associated conserved quantity. This theorem — known as Noether’s theorem after its discoverer, the incomparable mathematician Emmy Noether — is the root of why certain quantities are or aren’t conserved.

A time-translation symmetry leads to the conservation of energy, which explains why energy is not conserved in an expanding Universe. Spatial translation symmetry leads to the conservation of momentum; rotational symmetry leads to the conservation of angular momentum. Even CPT conservation — where charge conjugation, parity, and time-reversal symmetry are all combined — is a consequence of Lorentz symmetry.

Some symmetries are inherent to specific QFTs or to QFTs in general; some symmetries are inherent to specific solutions in GR or to GR in general. But these two descriptions of the Universe are both incomplete. There are many questions we can ask about reality that require us to understand what’s happening where gravity is important or where the curvature of spacetime is extremely strong (where we need GR), but also when distance scales are very small or where individual quantum effects are at play (where we need QFT).

These include questions such as the following:

• What happens to the gravitational field of an electron when it passes through a double slit?
• What happens to the information of the particles that form a black hole, if the black hole’s eventual state is thermal radiation?
• And what is the behavior of a gravitational field/force at and around a singularity?

To address them, GR and QFT individually are both insufficient. We need something more: an understanding of gravity at the quantum level.

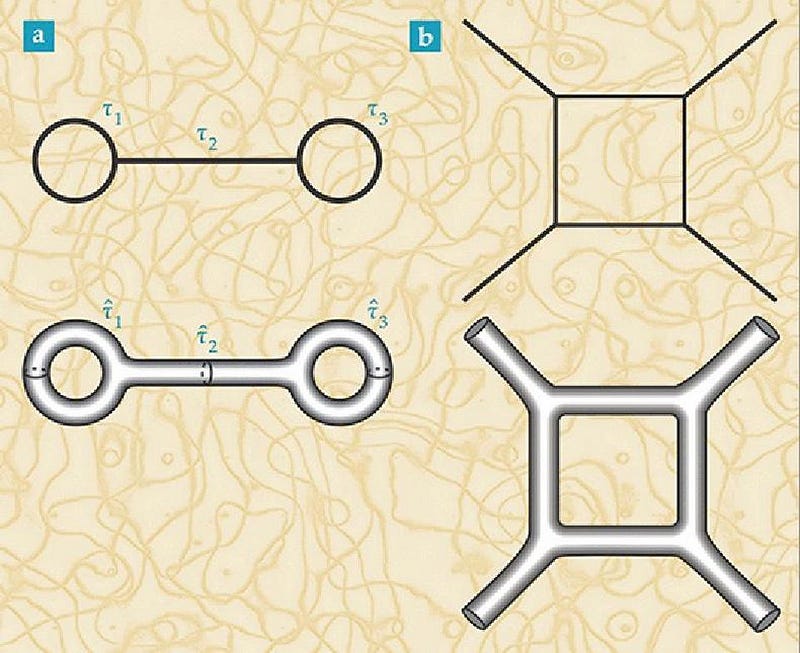
We don’t have a working theory of quantum gravity, of course, or we’d be able to understand what symmetries it does (and doesn’t) exhibit. But even without a full theory, we have a tremendous clue: the holographic principle. Just as a two-dimensional hologram encodes three-dimensional information on its surface, the holographic principle allows physicists to relate what happens in a spacetime with Ndimensions to a conformal field theory with N-1 dimensions: the AdS/CFT correspondence.

The AdS stands for anti-de Sitter space, which is frequently used to describe quantum gravity in the context of string theory, while the CFT stands for conformal field theory, such as the QFTs we use to describe three of the four fundamental interactions. While no one is certain whether this is applicable to our Universe, there are many good reasons to think it does.

The new result, which is very far-reaching in its implications, is this: within the framework of AdS/CFT, there are no global symmetries. The paper itself, published on May 17, 2019, is titled Constraints on Symmetries from Holography and was written by Daniel Harlow and Hirosi Ooguri. In particular, it showed that — again, within the context of AdS/CFT — that the following three conjectures are true.

1. Quantum gravity does not allow global symmetries of any type.
2. Quantum gravity requires that any internal gauge symmetry (which implies conservation laws like electric charge, color charge, or weak isospin) is mathematically compact.
3. Quantum gravity requires that any internal gauge symmetry necessarily comes along with dynamical objects that transform in all irreducible representations.

Each of these deserve elaboration, but the first one is the most powerful and profound.

All three of these conjectures have been around for a long time, and none of them are strictly true in either QFT or GR (or any form of classical physics) on their own. The classic arguments for all of them, in fact, are rooted in black hole physics and are known to require certain assumptions that, if violated, admit various loopholes. But if the AdS/CFT correspondence is true, and the holographic principle is applicable to quantum gravity in our Universe, all three of these conjectures are valid.

The first one means that there are no conservation laws that always necessarily hold. There might be good approximate conservation laws that are still valid, but nothing — not energy, not angular momentum, not linear momentum — is explicitly or strictly conserved under all conditions. Even CPT and Lorentz invariance can be violated. The other two are more subtle, but help extend global symmetries to local conditions: they held prevent things like the instantaneous teleportation of electric charge in one location to another, disconnected location, and require the existence of all possible charges allowed by the theory, such as magnetic monopoles.

The three quantum gravity conjectures that are demonstrated to hold for a holographic Universe have been around, in some form, since 1957, but they were only conjectures until now. If the holographic principle (and AdS/CFT, and possibly string theory, by extension) is correct, all of these conjectures are necessarily true. There are no global symmetries; nothing in the Universe is always conserved under all imaginable circumstances (even if you need to reach the Planck scale to see violations), and all non-forbidden charges must exist. It would be revolutionary for our understanding of the quantum Universe.

Despite the results and implications of this study, it’s still limited. We don’t know whether the holographic principle is true or not, or whether these assumptions about quantum gravity are correct. If it’s right, however, it means that once you include gravity, many of the symmetries that we hold so dear in the physics we know today are not global and fundamental. Paradoxically, if string theory is right, our expectations about hidden symmetries revealing themselves at a more fundamental level are not only wrong, but nature has no global symmetries at all.

Update: First author of the paper, Daniel Harlow, has reached out to clarify a point that was not sufficiently appreciated by the author. He relates the following:

I wanted to point out that there is one technical problem in your description… our theorem does not apply to any of the symmetries you mention here! And indeed in AdS/CFT they all can be unbroken. The reason is that they are all actually gauge symmetries, not global symmetries. For electric charge I guess you are familiar with that, but in gravitational theory such as general relativity then translations, Lorentz transformations, CPT, etc are also gauge symmetries: they are just diffeomorphisms.

The difference between a gauge symmetry and a global symmetry is that the presence of gauge charge can be measured from far away, while the presence of a global charge cannot. For example in elecromagnetism if we want to know the total charge in a region, we just have to measure the electric flux through its boundary. Similarly in gravity if we want to know the energy of something, we can measure the fall-off of the metric far away (basically looking for the M in the Schwarzschild metric). This should be compared with for example the Z_2 global symmetry of the Ising model, where there is no way to know that the spins are up in a region without going there and looking at them.

It isn’t widely appreciated, but in the standard model of particle physics coupled to gravity there is actually only one global symmetry: the one described by the conservation of B-L (baryon number minus lepton number). So this is the only known symmetry we are actually saying must be violated!

Send in your Ask Ethan questions to startswithabang at gmail dot com!