Ask Ethan: How Do Massless Particles Experience Gravity?
Einstein’s explanation is the only one that works.
When Newton first proposed the law of universal gravitation, it marked the very first time that we realized the same rule governing how objects fell on Earth also governed how they moved and attracted one another throughout the Universe. Objects fell to Earth because of gravity; Earth pulls itself into a spheroid because of gravity; moons orbit planets and planets orbit the Sun because of gravity; and so on to larger and larger scales. Newton’s law was simple but profound: objects with mass attract each other dependent only on their masses, distances, and the gravitational constant of the Universe. So how, then, do massless particles, like photons, experience gravity? That’s what Bret Hammers wants to know, asking:
Given the equation for gravity between two masses, and the fact that photons are massless, how is it possible for a mass (like a star or a black hole) to exert influence on said photon?
It’s a really good question, but one that our deepest understanding of gravity can answer. Let’s see how.
When Newton came along, his conception of gravity was radically revolutionary. People had previously measured how objects accelerated near the surface of Earth, with the distance they fell increasing in proportion to the time they were falling squared. Kepler had revolutionized astronomy by demonstrating that planets orbited the Sun in an elliptical orbit. And Halley, a contemporary of Newton, had begun to understand the periodic nature of comets.
Newton, incredibly, was able to synthesize all of this into a single framework. Objects fell at the rate they did on Earth because they accelerated towards the center of the Earth. Moons orbited their planets because of mutual attraction; same with planets and comets orbiting the Sun. A single, straightforward, simple law: the gravitational constant multiplied by any two masses, divided by the distance squared between them, gives you the gravitational force.
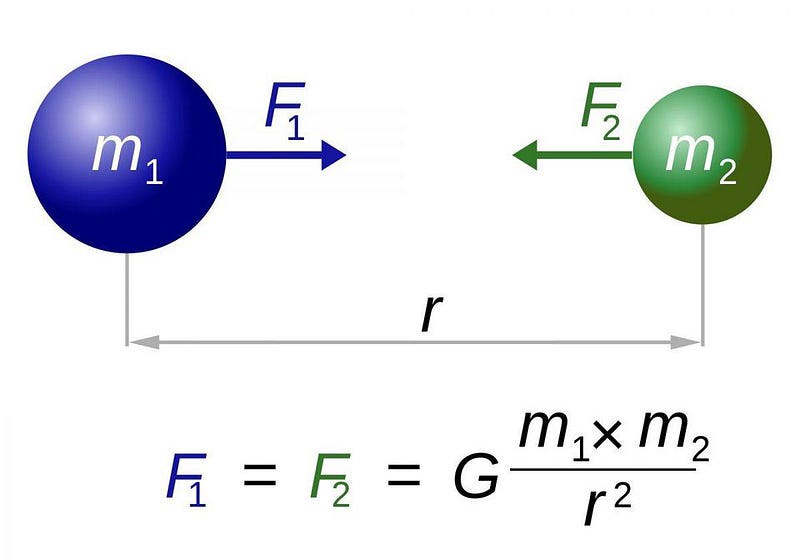
This explained all the different types of possible orbits: circles, ellipses, parabolas and hyperbolas. It explained gravitational potential energy, and how that potential energy would transform into kinetic energy. It explained escape velocity, and allowed us to eventually figure out how to escape the gravitational bonds of Earth. If there was a problem involving the gravitational force, Newtonian gravity could solve it. For some 200 years, it explained everything we ever observed.
The reasoning behind it was so simple, too: if you could state, with certainty and precision,
- what all the masses in the Universe were at any given time,
- where they were located,
- and how they were moving initially,
Newton’s gravity could tell you what the force would be on every object everywhere in the Universe at any point in time. The Universe, according to Newton, was completely deterministic.
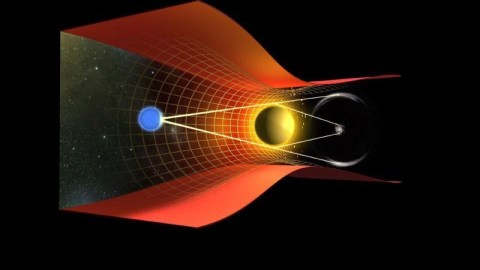
Here’s the basic idea of a Newtonian Universe: you have all your masses that exist, they attract one another, instantaneously, across any distance of space, for all time, with exactly the magnitude that Newton’s law of universal gravitation predicts. This is true for all masses everywhere at all times. If this were 100%, immutably true, there would be no way to reconcile this with light being bent by mass. Light is massless (m = 0), and therefore all the masses in all the Universe can exert no force on it. Anything, no matter how great, multiplied by 0 is still equal to 0.
But Newton’s picture cannot be right, and Einstein’s Special Relativity illustrates why. Imagine you and I are standing next to each other, and when a starting gun goes off, you race ahead, forward, while I stumble and remain at rest. When we look out at a distant mass, attracting us, you physically see a different distance to that mass than I do, even though we’re still at the same location in space.
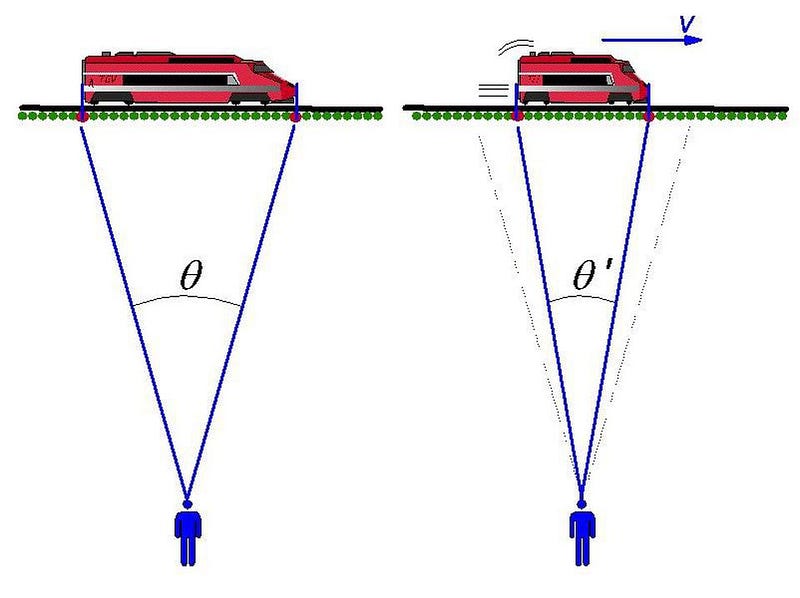
The reason for this is length contraction, which states that observers moving at different speeds will disagree about observed distances: the faster you go, the shorter (more contracted) lengths will appear to be. This is only one consequence of relativity, but it illustrates very well why the Newtonian picture cannot be true.
That distant mass that you and I see — with one of us stationary and the other one in motion — will exert a gravitational force on both of us. If we’re at the same distance from that object, physically, than the attractive force should be the same. But if distance is relative, then who is correct? Is my stationary measurement for the distances from the mass to us correct? Or is your in-motion measurement for the measurement, which is smaller, correct?

The answer, surprisingly, is that we need to both be correct. A correct law of gravity should be correct for whomever observes it, and Newton’s picture is incompatible with that. It took until 1915 for a more correct formulation to arise, and that was the arrival of Einstein’s General Relativity.
Conceptually, Einstein’s relativity doesn’t look very much like Newton’s picture. In particular, it asserts the following major differences.
- Space and time are relative, not absolute and fixed, and every observer’s views of them is equally valid.
- The entity of spacetime is deformed (or geometrically curved) by all the stresses on it.
- The cause of spacetime deformation is not merely mass, but all types of energy summed together, where mass is just one form of energy.
- And that changes to the curvature of spacetime can only propagate at the speed of gravity (which equals the speed of light), not instantaneously.
So, is Einstein right? Is Newton right? Are each of them partially right?
The whole reason Einstein’s relativity was proposed in the first place was that there was a problem in Newtonian gravity: it failed to correctly predict the changing motion of the planet Mercury’s orbit over time. There was an additional contribution needed, and Einstein knew he was onto something profound, at last, when his theory was able to reproduce those tiny deviations from Newton’s theory.
But there needed to be an additional test — where the two competing ideas made different predictions — that could tell them apart from one another.
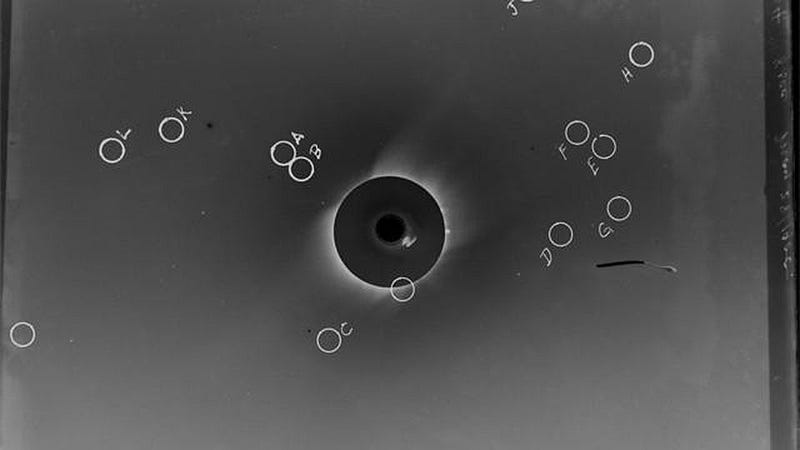
The first critical test was to use the Sun itself, and to see if it bent light or not. Those of you who saw the total solar eclipse of 2017 may have noticed a star, Regulus, only about a degree away from the eclipsed Sun. Stars are visible during many eclipses, and their path can appear to pass very close by the most massive object in the Solar System: our Sun. But would that light bend? Here were the three ideas:
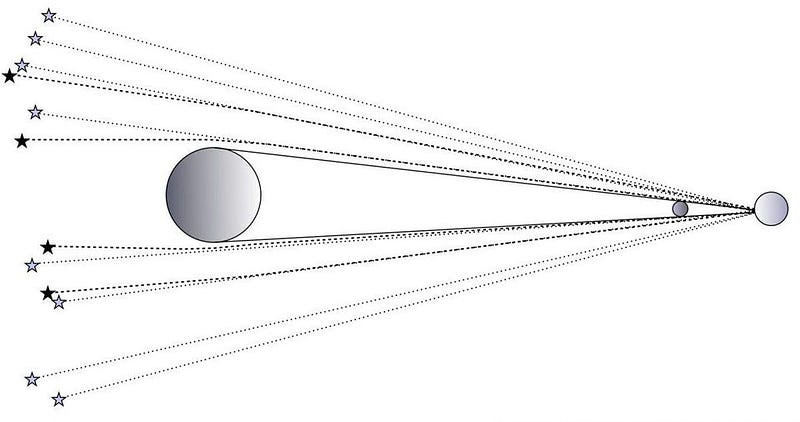
- If Newton was correct, and only masses attracted, then light wouldn’t bend at all; the apparent angular deflection would be zero.
- If Newton was part-right, and his law was true but you needed to assign photons an effective mass (because they have an energy, and we know that E = mc²), then you can assign them a mass of m = E/c², and calculate an apparent angular deflection.
- Or, if Einstein was wholly right, you would need to use his new theory of General Relativity to calculate the apparent angular deflection, which gives you a figure twice as large as the previous, semi-Newtonian deflection.
The total solar eclipse of 1919 had a number of observers set up around the world to take exactly these critical measurements. Known today as the Eddington expedition, after the British astronomer Arthur Eddington who masterminded the observational test, data was collected from the South American and African continents, and brought back together for analysis.
When the analysis was complete, even when the errors were included, the conclusion was clear: there was a deflection of starlight, and it was consistent with Einstein’s predictions. Newton’s theory of gravity doesn’t describe the Universe; you need Einstein’s General Relativity to get it right.

Today, we have a century of hindsight with respect to General Relativity and Newtonian gravity. We know that under almost all circumstances — as long as you’re not very close to a very large mass — Newtonian gravity is an excellent approximation to our better theory of gravity. But if you want to be more correct, you need to account for these typically small effects. The deviation of starlight from a straight line during the 1919 solar eclipse was just 0.0005°, but we were able to measure it to the necessary precision.

Masses aren’t the sole arbiter of gravitational attraction; all forms of energy contribute and are affected. The amount that they’re affected by is only approximately Newtonian, and where the differences get large, Einstein’s theory agrees with what we observe. Matter and energy curve spacetime, and curved spacetime tell both matter and energy how to move. That’s why masses can exert a gravitational influence on photons: they curve space. The photon has no choice of what it needs to do. It moves in a straight line from its perspective; it can’t help it if the Universe itself, because it contains matter and energy, isn’t made of straight lines at all!
Send in your Ask Ethan questions to startswithabang at gmail dot com!
Ethan Siegel is the author of Beyond the Galaxy and Treknology. You can pre-order his third book, currently in development: the Encyclopaedia Cosmologica.