Ask Ethan: Does Dark Energy Gravitate?

If all forms of energy experience gravitation, then why does dark energy make the expansion accelerate instead of slow down?
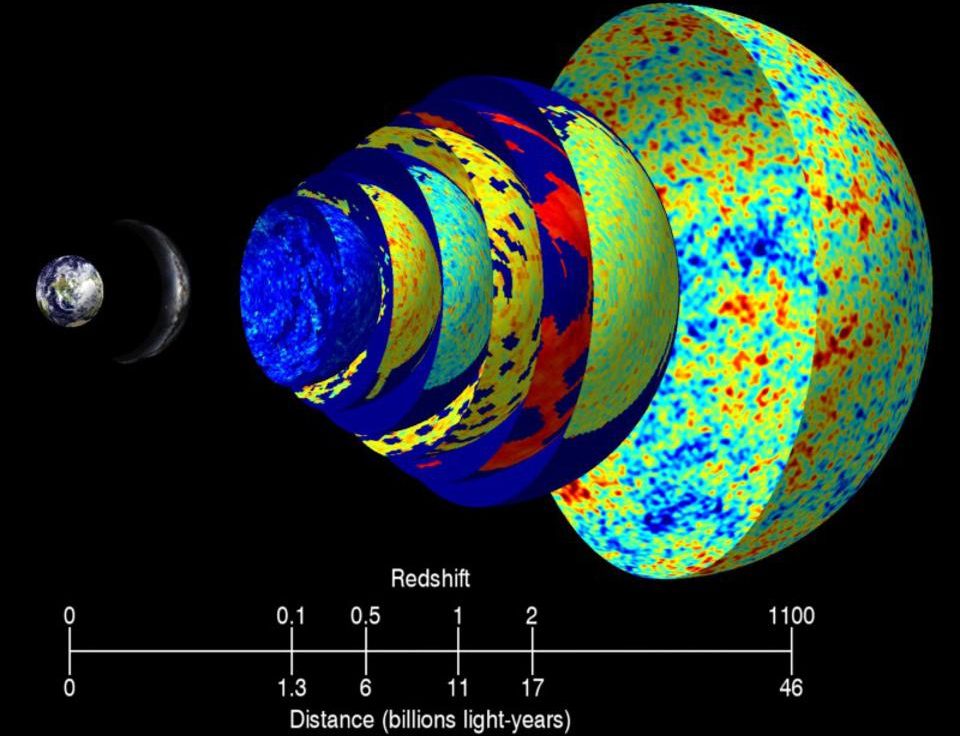
Of all the revolutionary discoveries that we’ve made about the Universe, the most unexpected and surprising has to be dark energy. A great cosmic race has been taking place ever since the Big Bang: between the initial expansion, working to drive everything apart, and gravitation, which works to pull everything back together. For billions of years, the Universe behaved as though these two opposing influences were in perfect balance.
Then, about 6 billion years ago, the expansion all of a sudden started speeding up again, causing distant objects to accelerate. Dark energy is the name we give to the unknown cause of this unexpected phenomenon, but suddenly things don’t add up quite so intuitively. That’s what Patreon supporter Stephen Peterangelo wants to know about, asking:
Does dark energy gravititate? In other words does the increase in dark energy as space expands also create more gravity?
The short answer is “yes,” but it’s not so intuitive. Let’s take a deep dive to see what’s really going on.
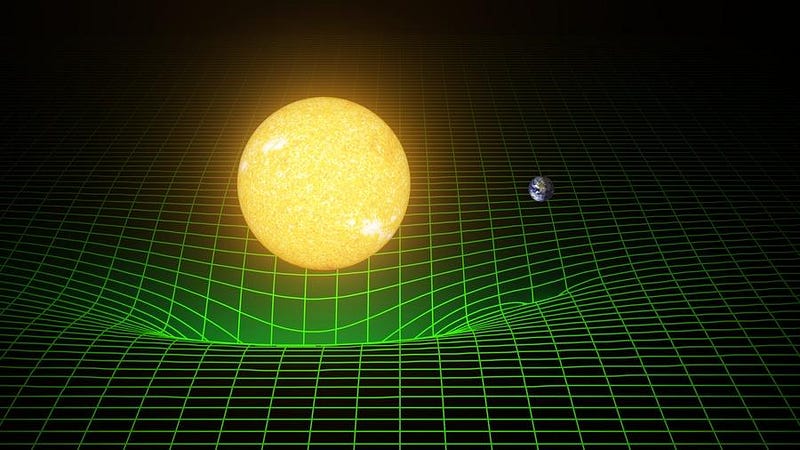
Every form of energy in the Universe, no matter how weird, exotic, or unfamiliar it is, obeys the same law of gravity: Einstein’s General Relativity. Most of the types of energy we’re used to come in the form of quanta: tiny little point-like packets of energy that move through the fabric of spacetime. Some of those quanta are radiation-like, meaning they move at the speed of light (or indistinguishably close to the speed of light). Others are matter-like, meaning they’re moving slow compared to the speed of light.
Some good examples are photons, which always act like radiation, normal matter and dark matter, which always act like matter, and neutrinos, which behave like radiation in the early Universe (or today, when they’re emitted by stars or other nuclear processes at high energies) but behave like matter later on, when the Universe has expanded and cooled sufficiently.

The reason for this dichotomy is that every particle has two types of energy it can possibly possess:
- rest-mass energy, which is the amount of energy inherent to the particle itself, via Einstein’s most famous equation, E = mc²,
- and kinetic energy, which is the energy due to the particle’s motion through the Universe.
As the Universe expands, the number of particles remains the same but the volume that they occupy — the size of the Universe — increases.
If we ask the question of how the matter density drops over time, it should dilute as the volume does: in proportion to the size of the Universe cubed. But if you have a lot of kinetic energy, or you’re something like a massless photon where your energy is defined by your wavelength, not only do you dilute with volume, but your wavelength also gets stretched as your Universe expands. Radiation, therefore, dilutes in proportion to the size of the Universe to the fourth power.
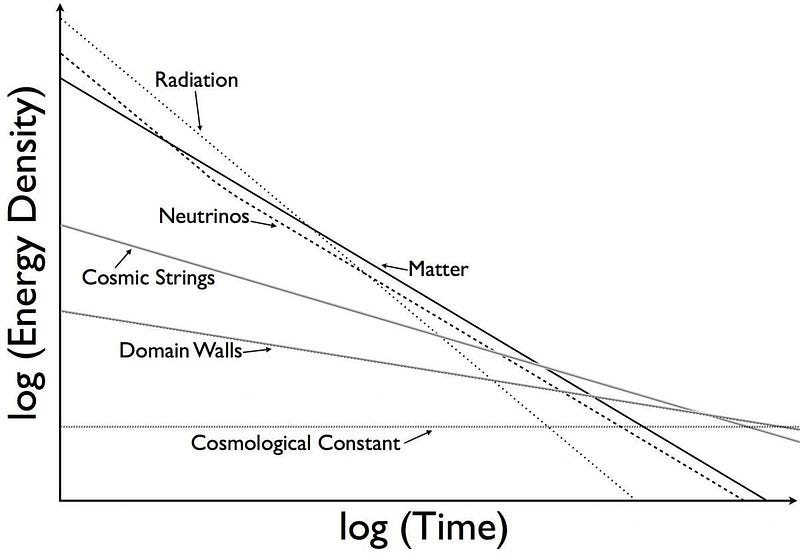
But there are other forms of energy the Universe is allowed to have besides particles. In particular, three different ideas have existed for a long time that all have energy, but all have their own evolution.
- Cosmic strings: which are long, thin, one-dimensional strands of energy that stretch across the Universe.
- Domain walls: which are long, thin, two-dimensional sheets of energy that stretch across the Universe.
- Cosmological constant: which is a form of energy that’s inherent to the fabric of space itself.
As the Universe expands, cosmic strings can still span the entire Universe in one dimension, but will take up less of the Universe’s volume in the other two. Domain walls can span the whole Universe in two dimensions, but will still dilute in the one other dimension. But for a cosmological constant, the fact that space is expanding just means that there’s more volume, and it doesn’t dilute at all. The energy density will remain a constant.
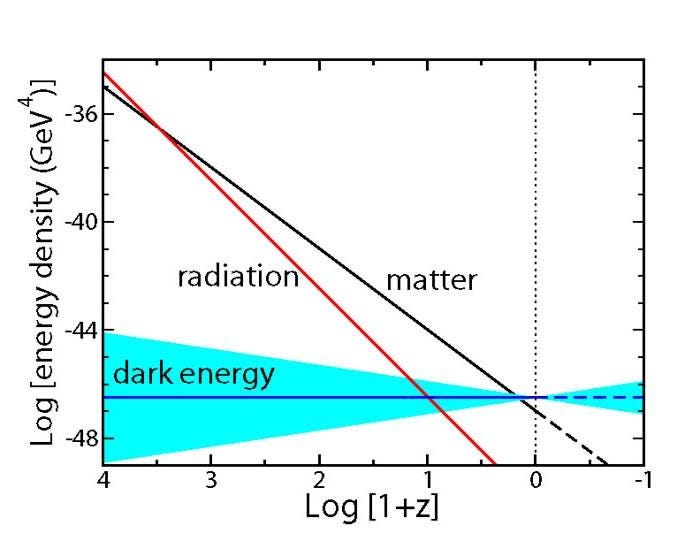
This is where most people begin to get puzzled. The simplest, most widely used candidate for dark energy — and also, the most consistent with the full suite of data — is that dark energy is a cosmological constant. The fact that we see the Universe expanding as it does means that there must be some new form of energy causing these distant galaxies to recede from us faster and faster as time goes on.
But if the energy present in the Universe is what causes gravity to work, as all the different forms of energy attract all the other forms of energy, then why are progressively more distant galaxies appearing to accelerate away from us as the Universe ages? This is a non-intuitive thing, after all! You’d think that if the Universe possessed a cosmological constant, it would be gaining energy as the Universe expanded, and would gravitate more, slowing the expansion rate down. But that isn’t what happens at all.
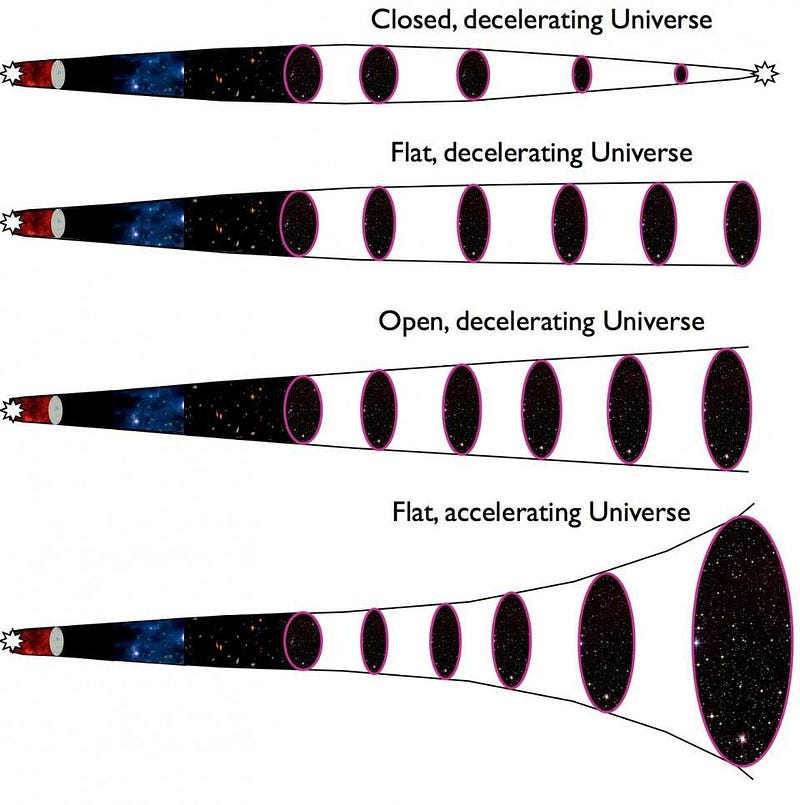
The big question, then, is why. Why does the presence of dark energy — either in the form of a cosmological constant or something very close to it — mean that distant galaxies are accelerating away from us at faster and faster speeds as the Universe continues to expand?
The answer, believe it or not, is because we live in a Universe governed by Einstein’s laws, and we have to follow what those laws tell us, even the parts of it that are counterintuitive. Einstein first put forth his greatest theory of all, General Relativity, in 1915. Immediately, people began working out the consequences of that theory. In 1916, Karl Schwarzschild worked out the solution for a non-rotating black hole. Other solutions soon followed: for an empty Universe; for gravitational waves; for a cosmological constant all by itself. But the most important advance came in 1922, when Alexander Friedmann derived the general solution(s) for a Universe filled with energy that was both isotropic (the same in all directions) and homogeneous (the same in all locations in space).

The two equations he derived are, even today, still known as the Friedmann equation, and fortunately we only need to examine the first one to learn how the Universe expands dependent on what forms of energy are in it. The first term in the equation — the leftmost one — is the Hubble expansion rate (squared): a measure of how quickly the fabric of space is stretching at any moment.
All of the other terms in the equation represent a combination of:
- all the matter,
- all the radiation,
- all the neutrinos,
- all the dark energy (which is the last term if it’s a cosmological constant),
- and all the forms of energy you can imagine,
followed by the penultimate term — the amount of spatial curvature — which is determined by how well-balanced or imbalanced all the forms of energy are with the expansion rate.
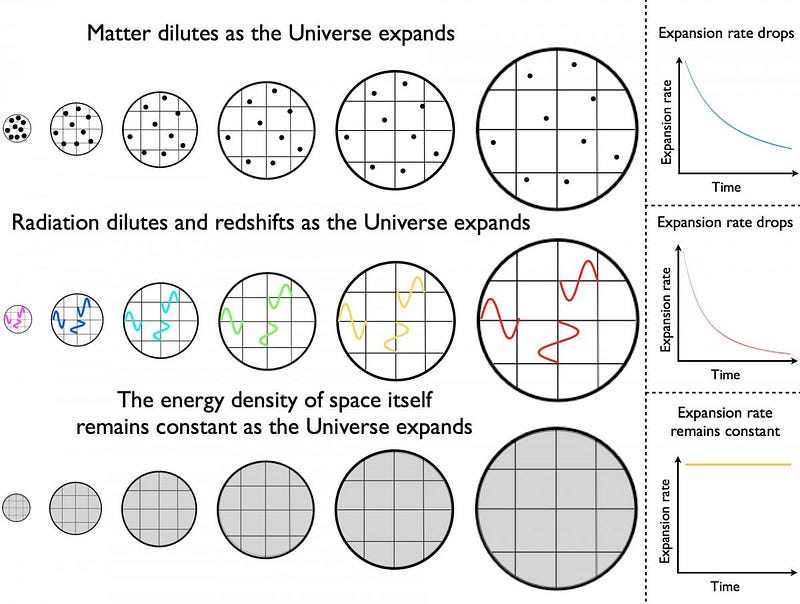
What this equation teaches us is that because the dark energy density remains a constant, the expansion rate will never drop below a certain amount if dark energy is real. The dark energy density term is a constant, so when the Universe expands enough that the density of everything else becomes negligible, the expansion rate will asymptote to a constant as well. For our Universe, this means that the expansion rate will never drop below about 55 km/s/Mpc: about 80% of its present value.
If dark energy didn’t gravitate, it couldn’t contribute to the energy density of the Universe or the Universe’s expansion. The first Friedmann equation shows us how the Universe expands, and how that expansion changes with time, but it doesn’t explain why. But the second Friedmann equation — which we use much less commonly — does: it’s General Relativity’s analogue of Newton’s F = ma, and it has a fundamental difference from how we normally think of things.
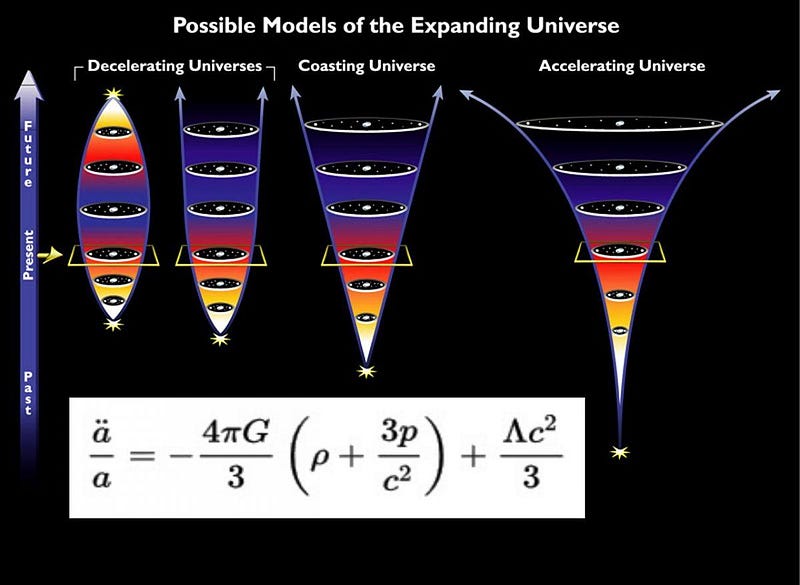
The biggest difference that you’ll notice immediately is that the way the expansion rate changes with time, which is encoded (in a complex way) in the second Friedmann equation, depends on not only the energy density, but the pressure of whatever you have in your Universe. For matter, the pressure is negligible so long as it’s moving slow compared to the speed of light. For radiation, the pressure is positive, meaning the expansion rate slows more quickly than it does for matter alone.
But for dark energy, the pressure is not only negative, it’s three times as powerfully negative as radiation pressure is positive. For dark energy, the pressure is actually equal to the negative of the energy density, so that the second derivative of the scale factor (which determines acceleration vs. deceleration) flips in sign from a matter or radiation-dominated Universe. Instead of decelerating, the Universe accelerates when dark energy dominates.
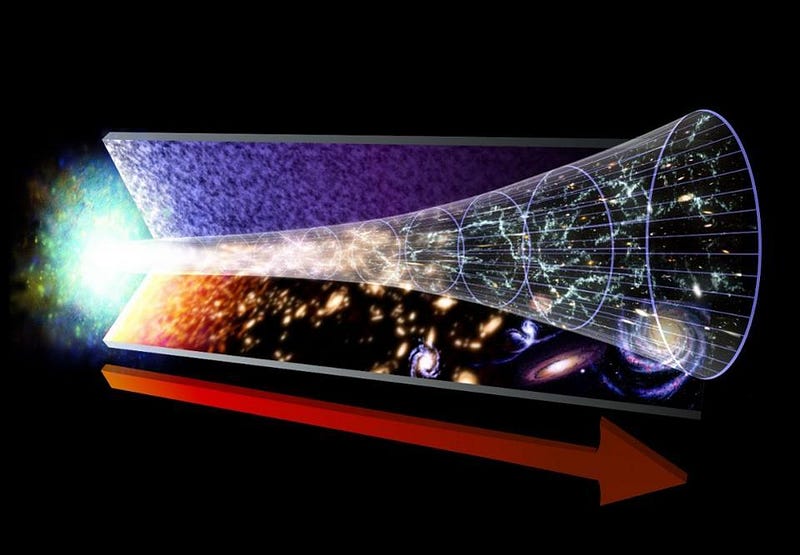
This leads to an even more counterintuitive result: as the Universe continues to expand, dark energy means that the total amount of energy contained within our observable volume always increases. Yet as it does, the Universe doesn’t decelerate, but rather speeds up. The most sacred laws in all of physics — the conservation of energy — only applies to particles interacting in a static spacetime. When your Universe expands (or contracts), energy is no longer conserved.
There is an amount of energy intrinsic to the fabric of space itself, but the effects of the energy density are overwhelmed by the effects of the negative pressure that arises. The Universe’s expansion doesn’t slow down due to the presence of dark energy, but rather distant galaxies will speed away faster and faster due to its cumulative effects. For anything beyond our Local Group, its fate is already sealed: it will speed away, faster and faster, until we can no longer access it in our accelerating Universe.
Send in your Ask Ethan questions to startswithabang at gmail dot com!
Ethan Siegel is the author of Beyond the Galaxy and Treknology. You can pre-order his third book, currently in development: the Encyclopaedia Cosmologica.